Backpropagation Step by Step

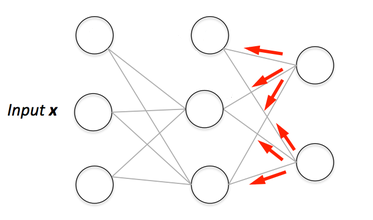独自のニューラルネットワークを構築する場合、それをトレーニングする方法を理解する必要があります。

フォワードパスとバックプロパゲーションの可視化はこちらをご覧ください。 netflow.jsを使ってニューラルネットワークを構築することができます。js

Overview

この記事では、3つの層を持つニューラルネットワークを構築します。

• 2つの入力ニューロンを持つ入力層
• 2つのニューロンを持つ1つの隠れ層
• 1つのニューロンを持つ出力層

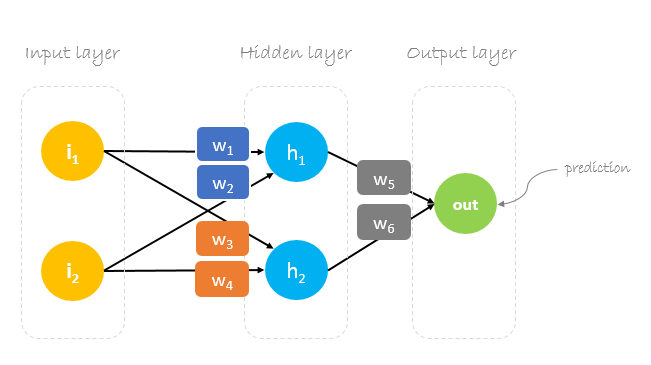
Weights, weights, weights

ニューラルネットワークのトレーニングは、予測誤差を最小化するような重みを見つけることです。 通常、ランダムに生成された重みのセットでトレーニングを開始し、バックプロパゲーションを使用して重みを更新し、任意の入力を出力に正しくマッピングしようとします。

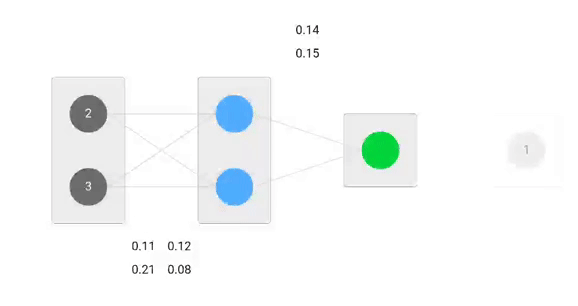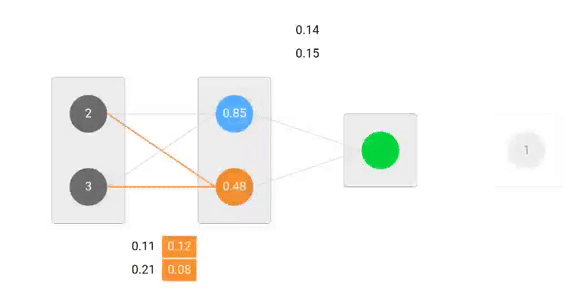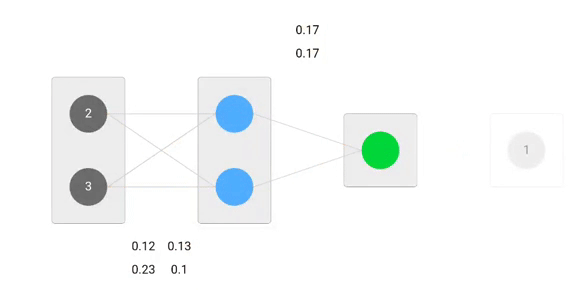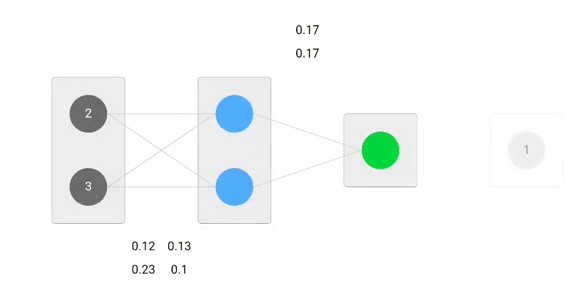
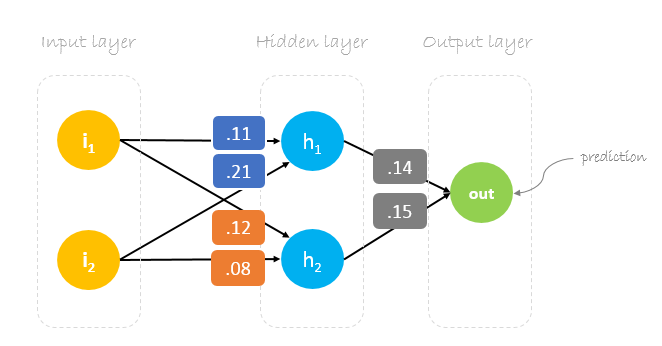
初期の重みは以下のようになります。w1 = 0.11w2 = 0.21w3 = 0.12w4 = 0.08w5 = 0.14 and w6 = 0.15

Dataset

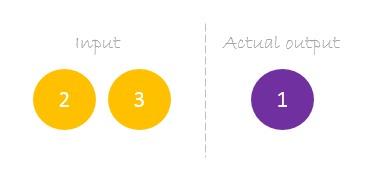
私たちのデータセットには、2つの入力と1つの出力を持つ1つのサンプルがあります。

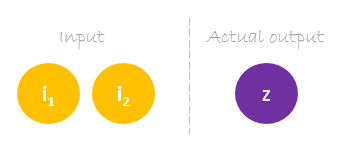
私たちの1つのサンプルは以下の通りです。 inputs=output=。

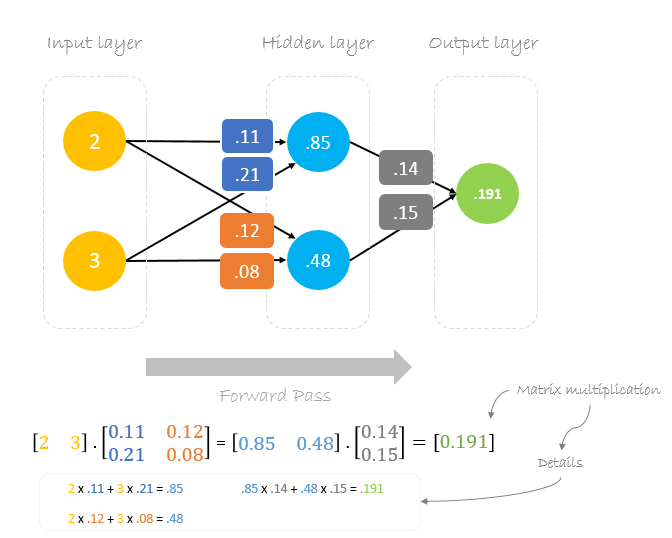
Forward Pass

与えられた重みと入力を使って出力を予測します。

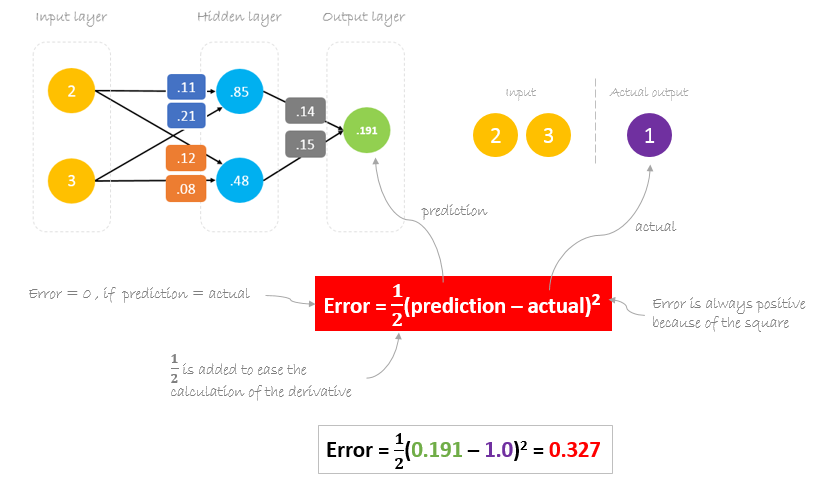
Calculating Error

さて、実際の出力と予測された出力の差を計算することで、私たちのネットワークがどのように機能したかを調べてみましょう。 ネットワークの出力 (予測) は、実際の出力に近いものではないことは明らかです。

Reducing Error

トレーニングの主な目的は、予測と実際の出力の間のエラーまたは差を減らすことです。 実際の出力は一定で、「変化しない」ため、誤差を減らす唯一の方法は、予測値を変更することです。

予測を基本的な要素に分解すると、予測値に影響を与える可変要素は「重み」であることがわかります。

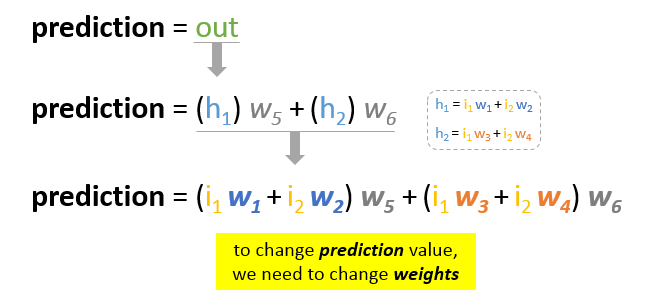
では、誤差を減らすために、どのようにして重みの値を変更するかという問題があります。

Backpropagation

Backpropagation（バックプロパゲーション）とは、「誤差の後方伝播」の略で、勾配降下法を用いて重みを更新するためのメカニズムです。 バックプロパゲーションでは、ニューラルネットワークの重みに対する誤差関数の勾配を計算します。

勾配降下法は、ある関数の最小値を見つけるための反復最適化アルゴリズムです。 勾配降下法を用いて関数の局所的な最小値を見つけるためには、現在の点における関数の勾配の負に比例したステップを踏みます。

例えば、w6w6w6w6 を基準とした誤差関数の偏導関数を減算します。 オプションとして、新たに更新されたウェイトがエラー関数を最小化していることを確認するために、エラー関数の微分に選択した数を掛けます。この数は学習率と呼ばれます。

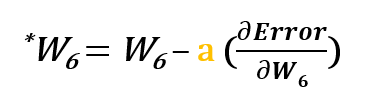
誤差関数の導出は、以下のように連鎖法則を適用して評価します。 w6に関する偏微分

だから、w6を更新するには、次の式を適用することができます

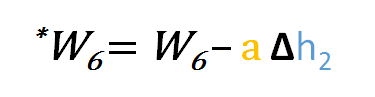
同様に、w5や、出力層と隠れ層の間に存在するその他の重みについても、更新式を導き出すことができます。

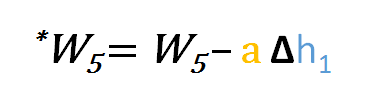
しかしながら、入力層と隠れ層の間に存在するw1w2w3w4w1に対する誤差関数の偏微分は以下のようになります。

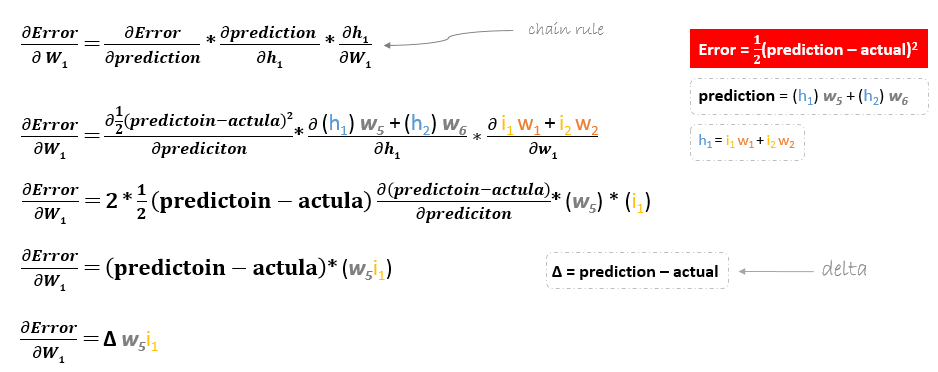
残りのウェイトw2w3w4についても、同様にして更新式を求めることができます。

要約すると、すべてのウェイトの更新式は以下のようになります。

更新式を行列で書き直すと以下のようになります

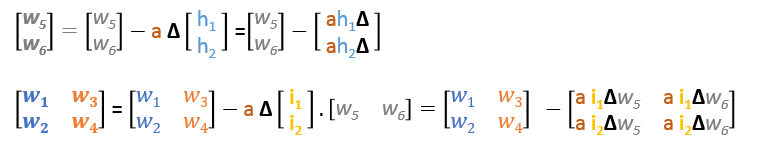
Backward Pass

派生した公式を使用して、新しい重みを見つけることができます。

「学習率」はハイパーパラメーターであり、その値を手動で推測する必要があることを意味します。

さて。

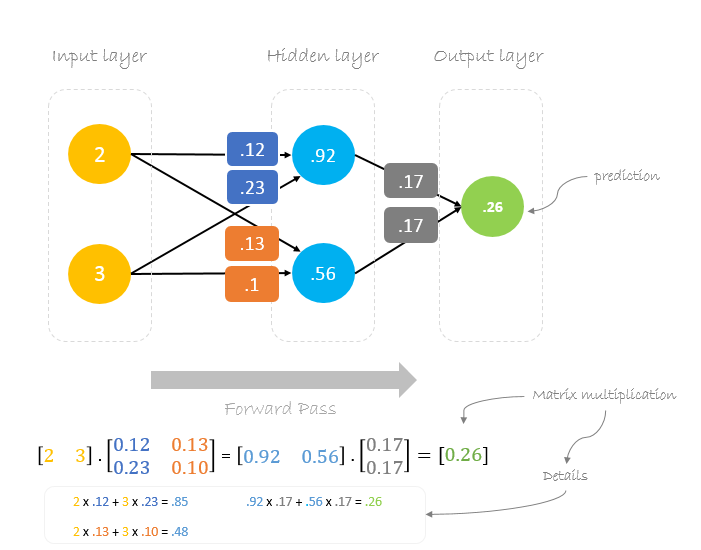
予測値0.260.191よりも、実際の出力に少し近いことがわかります。

バックプロパゲーションの視覚化

フォワードパスとバックプロパゲーションの視覚化を見ることができます。

netflow.jsを使用してニューラルネットワークを構築することができます