Chang Hsin Lee

分類問題のために機械学習モデルを構築するとき、自問自答する質問の1つは、なぜ私のモデルはくだらないのか？ モデルの開発は手榴弾を持っているようなものだと感じることがありますが、キャリブレーションは私の安全ピンの1つです。

Here’s link to the Jupyter notebook for this post

Evaluating probabilistic prediction

まず、キャリブレーションとは何か、そのアイデアはどこから来たのかを説明します。

機械学習において、ほとんどの分類モデルは、0から1の間のクラス確率の予測を生成し、その後、確率的な出力をクラス予測に変えるオプションを持っています。

二値分類の問題では、0と1の二値の出力の質を評価する、正確さ、精度、リコール、F1スコアなどの要約指標があります。 もし、出力が2値ではなく、0と1の間の浮動小数点数であれば、それをランキングのスコアとして使うことができます。

モデルの出力は、何かが起こる可能性を示すステートメントと見なすことができます。 このようなモデルの例として、私は毎日家を出る前にそのステートメントをチェックしていますが、気象庁があります。

image from weather.com

日曜日は80%の確率で雨が降ると言われています。 この80％というのはどのくらい信用できるのでしょうか？

つまり、正確な天気予報とは、80％の確率で雨が降ると予測されている日を100日調べた場合、80日前後は雨の日があるはずだということです。 また、他の確率の範囲でも正確でなければなりません。 30％の確率で雨が降ると言われている日は、100日のうち平均して30日は雨の日があるはずだ。 この天気予報サービスの予測がすべてこのような良いパターンであれば、その予測は校正されていると言えるでしょう。

• テストサンプルを予測された確率に基づいてビン分けしたときに、各ビンの真の結果がそのビンの確率に近い割合になっていれば、確率論的モデルは校正されていることになります。

  キャリブレーションのプロットは多くの場合、ラインプロットです。 ビンの数を選択し、予測値をビンに投入すると、各ビンはプロット上のドットに変換されます。 各ビンについて、y値は真の結果の割合であり、x値は平均予測確率です。 したがって、よくキャリブレーションされたモデルは、直線y=xに沿うキャリブレーションカーブを持っています。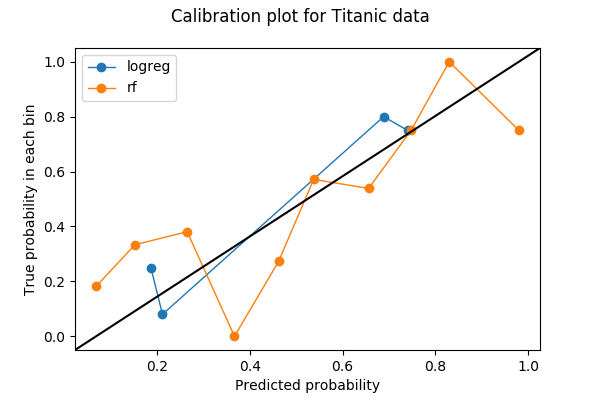

  

  このプロットをPythonでどのように作成したか、またその中で何を見たかをご紹介しましょう。

  Pythonの例

  キャリブレーション プロットを作成する際に最初に行うことは、ビンの数を選ぶことです。 この例では、確率を 0 から 1 の間の 10 のビン (0 から 0.1、0.1 から 0.2、…、0.9 から 1) に分割しました。使用したデータは Kaggle の Titanic データセットで、予測するラベルはバイナリ変数 SurvivedAgeSexSurvivedのクラス確率を生成します。

  +----+------+--------+| Age| Sex|Survived|+----+------+--------+|22.0| male| 0||38.0|female| 1||26.0|female| 1|+----+------+--------+

  前処理

  モデルをトレーニングする前に、AgeSexを値0と1を持つ数値変数にしました。

  import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn import preprocessingfrom sklearn import model_selectiontitanic = pd.read_csv('train.csv')fitted_age_imputer = preprocessing.Imputer(axis=1).fit(titanic.values)titanic = fitted_age_imputer.transform( titanic.values.reshape(1, -1) ).transpose()titanic = np.where(titanic.Sex == 'female', 1, 0)

  続いて、データをトレーニングセットと検証セットに80/20の割合で分割しました。

  from sklearn import model_selectionfeature_cols = feature_train, feature_test, label_train, label_test = ( model_selection.train_test_split( titanic, titanic.Survived, test_size=0.2, random_state=1) )

  訓練と予測

  これで、訓練セットでロジスティック回帰モデルを訓練し、検証セットで予測することができます。

  from sklearn.linear_model import LogisticRegressionlogreg_model = LogisticRegression().fit(X=feature_train,y=label_train)logreg_prediction = logreg_model.predict_proba(feature_test)

  同様に、ランダムフォレストモデルを訓練し、検証セットで予測します。

  from sklearn.ensemble import RandomForestClassifierrf_model = RandomForestClassifier(random_state=1234).fit(X=feature_train, y=label_train)rf_prediction = rf_model.predict_proba(feature_test)

  正のクラス確率は、2列目のモデル（index=1）が返します。

  logreg_prediction

  array(, , , , ])

  キャリブレーションプロット

  クラスの確率とラベルが得られたら、キャリブレーションプロット用のビンを計算することができます。

  from sklearn.calibration import calibration_curvelogreg_y, logreg_x = calibration_curve(label_test, logreg_prediction, n_bins=10)

  ロジスティック回帰のために10個のビンを求めましたが、10個のうち6個のビンにはデータがないことに注意してください。 その理由は、ロジスティック回帰が単純なモデルであること、特徴が 2 つしかないこと、検証セットのデータが 200 ポイント未満であること、などが組み合わさっています。

  ), array()]

  次に、ランダムフォレストモデルのビンの座標を計算します。

  rf_y, rf_x = calibration_curve(label_test, rf_prediction, n_bins=10)

  これで、2つの検量線をプロットすることができました。 プロットを読みやすくするために、StackOverflowの回答に基づいて、y=xの参照線も追加しました。

  %matplotlib inlineimport matplotlib.pyplot as pltimport matplotlib.lines as mlinesimport matplotlib.transforms as mtransformsfig, ax = plt.subplots()# only these two lines are calibration curvesplt.plot(logreg_x,logreg_y, marker='o', linewidth=1, label='logreg')plt.plot(rf_x, rf_y, marker='o', linewidth=1, label='rf')# reference line, legends, and axis labelsline = mlines.Line2D(, , color='black')transform = ax.transAxesline.set_transform(transform)ax.add_line(line)fig.suptitle('Calibration plot for Titanic data')ax.set_xlabel('Predicted probability')ax.set_ylabel('True probability in each bin')plt.legend()plt.show()

  

  ビンの合計と識別

  ロジスティック回帰では10ビンを求めたところ、4つの空でないビンしかありませんでした。 これは悪いことなのでしょうか？ sklearn.calibration.calibration_curveのソースコードから取った関数を使って、どのビンが欠損ビンなのかを調べてみましょう。

  def bin_total(y_true, y_prob, n_bins): bins = np.linspace(0., 1. + 1e-8, n_bins + 1) # In sklearn.calibration.calibration_curve, # the last value in the array is always 0. binids = np.digitize(y_prob, bins) - 1 return np.bincount(binids, minlength=len(bins))bin_total(label_test, logreg_prediction, n_bins=10)

  array(, dtype=int64)

  欠落しているビンの中点値は、5%、35%、45%、55%、85%、95%です。

  識別は、分類問題において、キャリブレーションと隣り合わせの概念です。 モデルを構築する目的が、統計的な推定値を提供することではなく、自動的な決定を行うことである場合、識別は較正よりも先に行われることもあります。

  • モデルAは、どの日も10%の確率で雨が降ると言っています。
  • モデルBは、6月は毎日雨が降り(100%)、他の11ヶ月は雨が降らない(0%)と言っています

  モデルAは完全にキャリブレーションされています。 1つのビン (10%のビン) しかなく、真の確率は10%です。 しかし、モデルBは、100%のビンには30日、0%のビンには6日の雨の日があるため、キャリブレーションが少しずれています。 しかし、週末にハイキングの計画を立てる場合には、モデルBの方が明らかに便利です。

  識別性は多くの場合、受信者動作特性曲線 (ROC 曲線) でチェックされますが、これは別の投稿のトピックです。

  クロスバリデーション

  識別性を気にせず、優れたキャリブレーションのみを求める場合、ロジスティック回帰 (青) はランダム フォレスト (オレンジ) よりも優れているように見えます。 これは本当にそうなのでしょうか？

  bin_total(label_test, rf_prediction, n_bins=10)

  array(, dtype=int64)

  いくつかのビンのデータポイントが少なすぎることが問題なのではないかと考えています。

  前のプロットではデータの 20% しか使用されていませんでしたので、もっと使用できるかもしれません。 異なるモデル間のキャリブレーションをテストする際にすべてのデータを使用するには、クロスバリデーションからアイデアを盗むことができると考えました。 クロスバリデーションのためにデータを5つのフォールドに分割すると、各フォールドは一度だけ検証セットとして使用されます。 そのため、5つのフォールドすべての予測確率を連結し、それをもとにキャリブレーション・プロットを作成することができます。 5フォールドのキャリブレーション・プロットの結果は、以下のようなプロットになります。 コードはJupyter notebookの最後のセクションにあります。

  

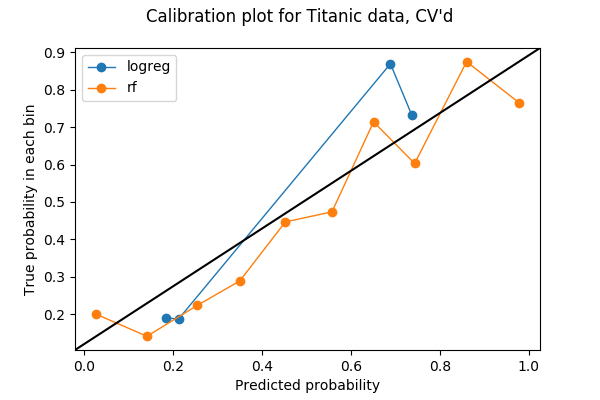
  各ビンがより多くのポイントを持つようになりました：

  array(, dtype=int64)

  そして、この例では、ランダムフォレストがロジスティック回帰よりも優れたキャリブレーションを行っていると言ってもいいと思います。

  ***

  Nate Silver氏は、『The Signal and the Noise』という本の中で、天気の校正に関する素晴らしい例を紹介しています。同氏は、第4章『For Years You’ve Been Telling Us That Rain Is Green』の中で、国立気象局、天気予報チャンネル、地元のニュース チャンネルという 3 つのソースからの予測を研究しました。 彼は、ほとんどのローカル・ニュース・チャンネルは調整不足で、「雨」であると結論づけています。 これは珠玉の一冊で、手に入るなら手に取ってみることをお勧めします。

  私がキャリブレーションについて初めて知ったのは、2016年に同僚のケビンを通じて、分類モデルに関するいくつかのメトリクスについて議論したときでした。 彼がいなければ、私がキャリブレーションの重要性に気づくまでには、おそらくさらに1年か2年かかり、この記事を書くまでにはもっと時間がかかっていたでしょう。