Horizontal Stretch -Properties, Graph, and Examples

似たようなグラフでも幅が違うものに出会ったことがあるかもしれません。 これらの関数は、基底関数を使用して水平方向に伸張されている可能性があります。

水平方向の伸縮は、基底グラフがX軸に沿ってY軸から離れる方向に広げられたときに起こります。

グラフを水平方向に伸ばす方法を学ぶことは、関数のグラフのファミリーを理解するのに役立ちます。

次のセクションに移る前に、親関数、変換、垂直伸張の知識を復習しておいてください。

• 遭遇する可能性のある一般的な親関数を理解する
• 垂直および水平変換の知識を再確認する
• 垂直伸張を適用する方法を復習する。

これらのリンク先の記事で知識をリフレッシュし、準備ができたら、水平方向のストレッチについてもっと学んでみましょう。

関数に水平ストレッチを適用するには、その入力値にスケール ファクター a を掛けます。 これは、f(x)などの関数ではどうなるでしょうか。

それでは、f(x)=x2のスケールファクターが1/2と1/3の場合に、どのような影響を受けるかを見てみましょう。

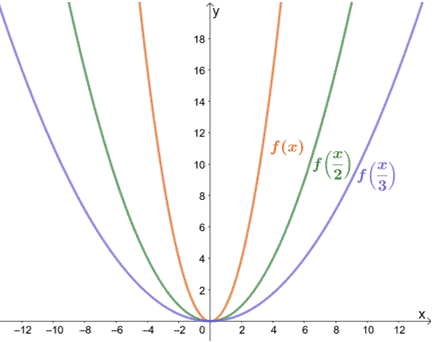
予想通り、グラフは2倍と3倍に伸びました。 Y値が同じであることに注目してください。 これは、すべての水平方向の伸びに当てはまります。

他の関数の水平方向の伸縮も同様の特性を示します。 例えば、f(x)=｜x｜とすると、この関数のグラフを水平方向に伸ばしてg(x)とすると、新しい関数の式は｜1/3 ∙ x｜ =｜x/3｜と表すことができます。

両方の関数からいくつかの値を比較してみませんか？

td

x	-2	-?1	0	1	2
f(x) = |x|	2	1	0	1	2

また、すべてのx-座標が3増加することを期待します。座標が3増加することを期待します。 これを行うと、出力値は同じになります。

td

となります。

x	-6	-?3	0	3	6
g(x)=｜x/3｜	2	1	0	1	2

このことは、新しい関数のグラフの座標にどのような意味があるのでしょうか。

How to horizontally stretch a function?

水平方向の伸縮とそれが基底関数にどのように影響するかを学んだので、今度はそれを関数のグラフに適用してみましょう。

• Y座標が同じ位置に残るように、グラフの底辺を水平に伸ばすだけにします。
• Y座標が変わらないので、Y切片も変わりません。
• 切片や最大点など、グラフ上の重要なポイントを再確認してください。
• 座標点が正しくスケーリングされているかどうかも確認してください。

前のセクションで示した値の表を使用して、y = |x| と y = |x/3| の両方をグラフ化し、グラフ上の水平方向の伸縮の効果を視覚化してみましょう。

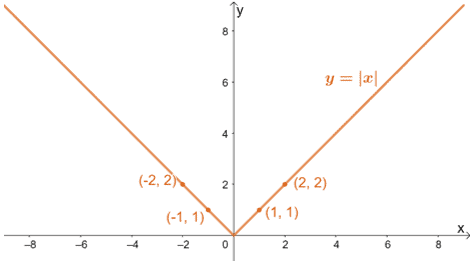
これまで説明してきたように、y の値が一定のままで、グラフが底辺に沿って伸びることが予想されます。

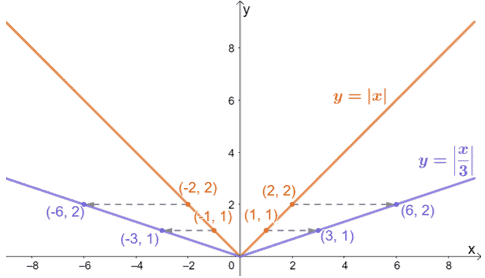
y = |x/3|を得るためには、親関数y = |x|を3倍に伸ばします。 上のグラフで確認できますが、他の関数のグラフを水平方向に伸ばす際にも同じプロセスを適用できます。

水平ストレッチの定義と特性のまとめ

水平ストレッチを伴う問題に答えたり、関数をグラフ化したりする際に覚えておくべき重要なポイントは以下のとおりです：

• 入力値もaだけ増加するとき、グラフを1/aの係数で水平ストレッチすることしかできません。
• f(x)をf(ax)に水平に引き伸ばすとき、x座標にaを掛けます。
• y切片の位置はそのままです。
• 結果として得られる関数は、範囲は同じですが、ドメインは異なるかもしれません。
• ある点(m, n)を水平に伸ばすと(am, n)になる

迷ったときはこの5つのポイントに立ち返ってみましょう。

自分の知識を試す準備はできましたか？

例題1

関数g(x)は、f(x)=8xを1/4の縮尺で水平に伸ばして得られます。 g(x)の式として正しいものはどれか

a. g(x)=32x
b. g(x)=16x
c. g(x)=2x
d. g(x) =1/2 x

解答

関数を1/aで水平に伸ばすとき、入力値をaで割ることを覚えておいてください。

g(x) = 8(x/4)

式を単純化するとg(x) = 2xとなります。

例題2

以下の条件でg(x)とh(x)の式をf(x)から書きます。

a. 関数g(x)はf(x)を1/5倍に水平に伸ばした結果である。

解答

まずg(x)から見てみましょう。 f(x)を水平に伸ばすとg(x)が得られるので、f(x)の入力値を5で割ってg(x)の式：f(x/5)を求めます。

g(x)が得られたので、h(x)の式を求めます。

h(x)=g(x/2)

= f(x/5 -1/2 )

= f(x/10)

これにより、f(x)に関しては、g(x)=f(x/5)、h(x)=f(x/10)となります。

例3

関数f(x)は点(6, 4)を通過します。 f(x)をスケールファクター1/2で水平方向に伸ばした場合、その点の新しいx座標は何になるでしょうか。

解答

グラフを水平方向に引き伸ばすとき、基本関数のx座標に与えられたスケールファクターの分母をかけて、同じy座標に沿った新しい点を求めます。

したがって、(6, 4)→(2∙ 6, 4)となります。

例題4

f(x)の値の表を以下に示します。 h(x)がf(x)をスケールファクター1/4で水平方向に伸ばした結果である場合、その値の表を作成し、現在の出力値を保持します。

です。

です。 です。

x	-3	-2	-?1	0	1	2	3
f(x)	-。6	-4	-??2	0	2	4	6

解決策

関数を横に伸ばした場合。

関数を横に伸ばす際には、入力値（ここではxの値）に、与えられたスケールファクターの分母を掛けます。

つまり、(-2, -4) は、(4∙ -2, -4) = (-8, -4) に変換されます。 残りの値についても同様の処理を行い、h(x)の値の表を以下のように作成します。

です。

x	-12	-8	-?4	0	4	8	12
h(x)	-。6	-4	-2	0	2	4	6

例題5

以下に示す関数を見てください。 f(x)とg(x)の関係はどうなっていますか？

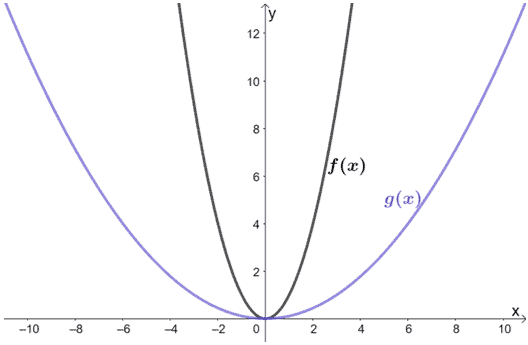
解答

グラフを見ただけでは、f(x)を水平に伸ばした結果がg(x)であることがわかります。 では、両方のグラフからいくつかの点を調べてみましょう。

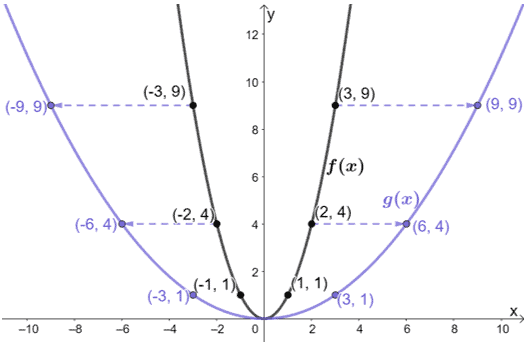
これがポイントに起こることです。

• (-3, 9)→(-9, 9)
• (-2, 4)→(-6, 4)
• (-1, 1)→(-3, 1)
• (0, 0)→(0, 0)
• (1, 1)→(3, 1)
• (2, 4)→(6, 4)
• (3, 9)→(9, 9)

それぞれの場合において、g(1, 1)のx座標がどのようになっているかに注目してください。 g(x)のx座標は、すべてf(x)の3倍になっています。

関数g(x)はf(x)を1/3の縮尺で水平に伸ばした結果です。

例6

下の図はf(x)のグラフです。 g(x)は、f(x)を水平方向に1/2倍に伸ばした結果であることを利用して、グラフを作成しなさい。

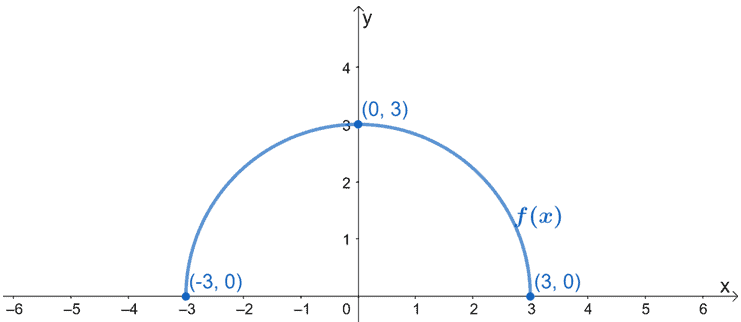
解答

先にg(x)の新しい臨界点を求めてみましょう。

• (-3, 0)→(-6, 0)
• (0, 3)→(0, 3)
• (3, 0)→(6, 0)

これらの点をプロットして、f(x)のグラフを3倍に伸ばします。

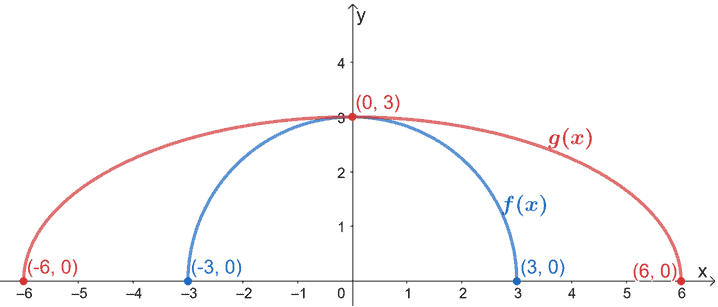
このようにしてできたグラフを見てみましょう。 g(x)はf(x)を横に伸ばした結果なので、f(x)のグラフを3倍に伸ばします。

例題7

以下の関数に対して行われた変換を説明します。

a. f(x) = x2 → g(x) = x2/9

b. m(x) = √x → n(x) = 3√(x/4)
c. p(x) = 3x – 1 → q(x) = 3x/4 – 2

解答

水平方向の伸びだけではないものがあることに気付いたかもしれませんが、その通りです!

特定の関数の式を得るためには、異なる変換技術を適用しなければならないことがあることを覚えておいてください。

まず、f(x)とg(x)について説明します。

g(x)を得るためにf(x)の入力値に適用されたスケールファクターを確認するために、g(x)を完全な二乗として表現します：g(x)=(x/3)2 = (1/3 – x)2

g(x)をf(x)で表現すると、g(x)=f(x/3)となります。

続いて、m(x)とn(x)について説明します。

n(x)には、出力値に3、入力値に1/4という2つのスケールファクターが適用されています。 垂直方向と水平方向の伸縮についての知識を適用すると、n(x)=3-m(1/4 – x)となります。 つまり、n(x)は、m(x)が垂直方向に 3 のスケール ファクターで引き伸ばされ、水平方向に 1/4 のスケール ファクターで引き伸ばされた結果であるということです。

q(x) = 3/4 x – 1 – 1

= 3(x/4) – 1 – 1

= p(x/4) – 1

このことから、q(x)は、p(x)が水平方向に1/4倍に引き伸ばされ、下方向に1単位変換された結果であることがわかります。

例題8

g(x)=2|x/3| – 1となるように、f(x)にはどのような変換が行われているでしょうか。 以下のf(x)のグラフを参考にしてください。

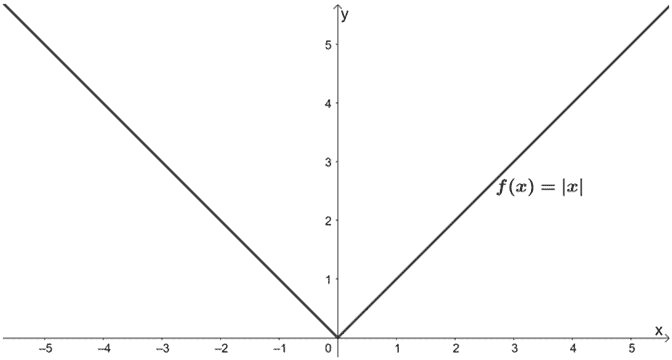
解答

早速、g(x)をf(x)で表してみましょう。

g(x) = 2 – |1/3 – x| – 1

= 2- f(x/3) – 1

これは、g(x)を得るためのf(x)の平行移動が次のようになることを意味しています:

• 水平方向に1/3のスケールファクターで引き伸ばす。
• 縦に縮尺 2 倍。
• 下に 1 単位移動。

f(x)を水平に伸ばすことから始めて、f(x)にこれらの変換をゆっくりと適用していきましょう。

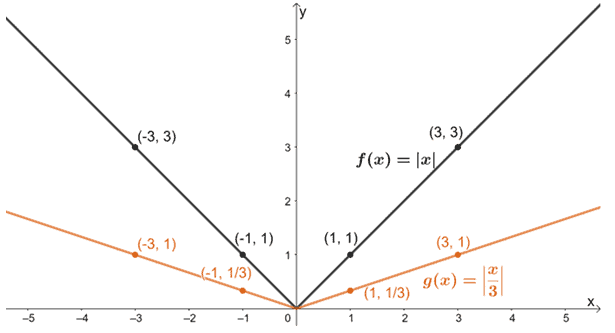
それでは、できあがったグラフをスケールファクター2で垂直方向に伸ばしてみましょう。

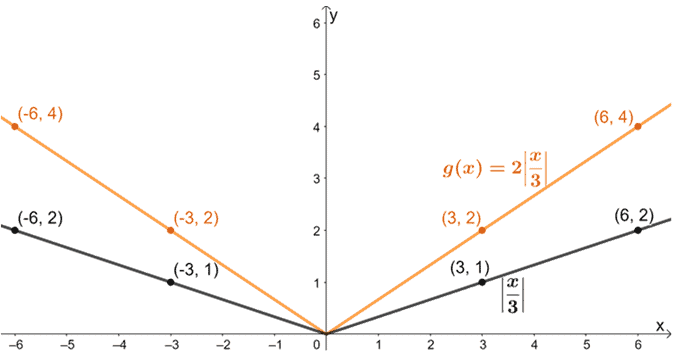
最後に、グラフを1単位下向きに変換してみましょう。

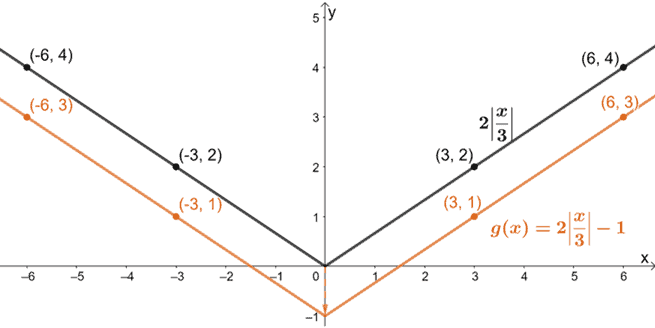
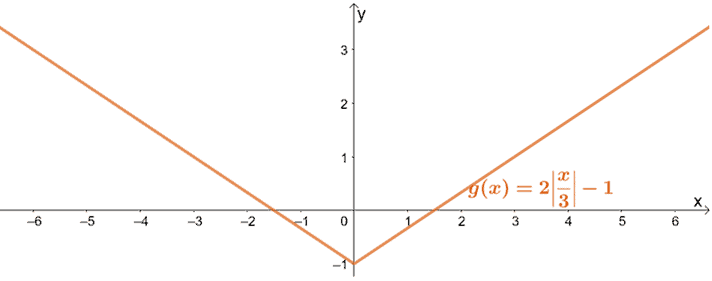
以上、g(x)を絶対値関数の親関数であるf(x)=｜x｜を使ってグラフ化する方法を示しました。

練習問題

1. 関数g(x)は、f(x)=16×2をスケールファクター2で水平に伸ばして得られます。 g(x) = 32×2

b. g(x) = 16×2

c. g(x) = 8×2

d. g(x) = 2×2

2. 以下の条件で、g(x)とh(x)の式をf(x)を基準にして書いてみてください:

a. 関数g(x)は、f(x)を1/4倍に水平に伸ばした結果である

b. 関数g(x)は、f(x)を水平方向に1/3倍に伸ばしたものです。

3. 関数f(x)は点(10, 8)を通ります。 f(x)をスケールファクター5で水平に伸ばした場合、その点の新しいx座標は何になるか？

4.f(x)の値の表は以下の通りである。 g(x)がf(x)をスケールファクター3で水平方向に伸ばした結果である場合、その値の表を作成し、現在の出力値を保持しなさい。

です。

x	-9	-6	-?3	0	3	6	9
f(x)	-。17	-11	div5	1	7	13	19

5. 以下に示す関数を観察する。 f(x)とg(x)の関係はどうなっていますか？

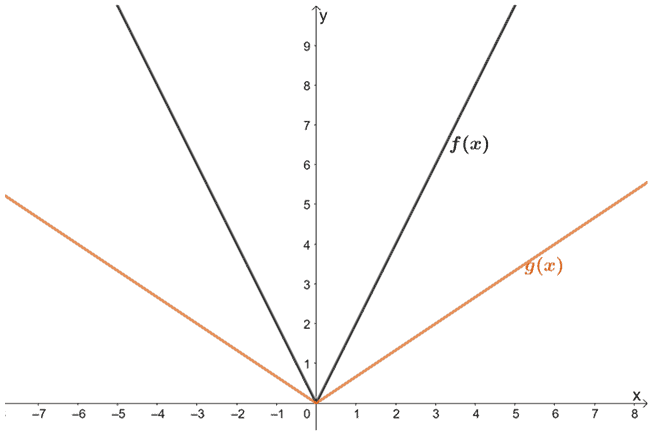
6.下の図はf(x)のグラフです。 h(x)は、f(x)が水平方向に1/3倍に引き伸ばされた結果であることを利用して、グラフを作成しなさい。

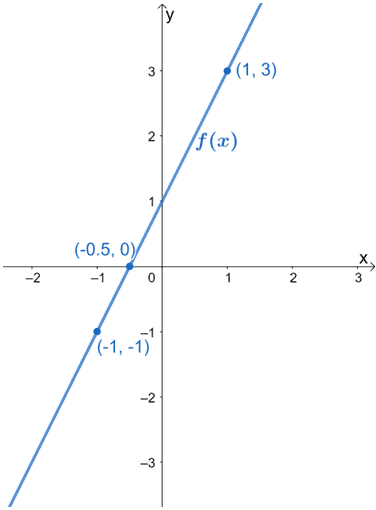
7.次のような関数の変換について説明してください。 f(x) = x2 → g(x) = x2/16

b. m(x) = √x → n(x) = √(x/5) + 3

c. p(x) = 2x + 1 → q(x) = 2x/3 + 2

8. g(x) = 3√(x/2)となるように、f(x)に対して行われる変換は何か。 以下に示すf(x)のグラフを参考にしてください。

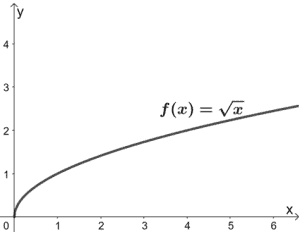
画像・数学的な図面はGeoGebraで作成しています。