Tension Calculator

How to calculate tension in ropes suspending an object

下の図を見ると、物体を持ち上げるのに必要な力Fは、物体の重さWに等しいことがわかります。 この考え方は、引張力の公式を支える基本的な概念です。 また、下の図は、物体の自由胴体図で、ひもに働く引張力Tを示しています。 ご覧のように、張力はペアで、しかも反対方向にかかっています。

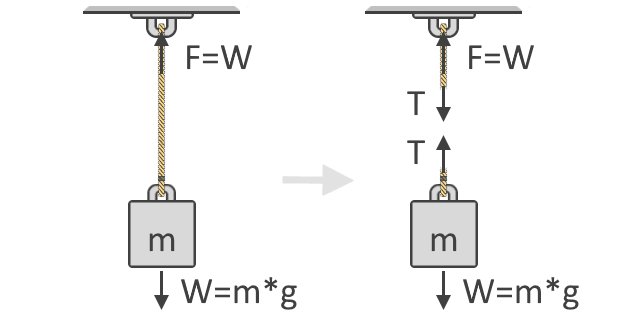
ニュートンの運動の第2法則に従うと、物体に働く力の総和を表すことができます。 上の図の右側のように、物体の自由胴体図を使って、力の総和を表すことができます。 自由体積図は、物体に働く力の方向と大きさを示すために使用します。 平衡状態では、これらの力はすべてゼロになるはずです。 上向きの力をプラス、下向きの力をマイナスと考えると、次のような式になります。

ΣF = 0 = T + (-W)
T = W
ここで、重さのWは下向きなのでマイナスになります。

物体を持ち上げるために、より多くのロープを使用すると、全体の引張力はロープに分割されます。

また、複数のロープを使って物を持ち上げると、その分の張力が各ロープに分配されますが、各ロープの張力は、対抗する力の方向に対する角度によって決まります。 このことをさらに理解するために、2本のロープで物体を吊るした場合の別の自由体図を考えてみましょう（下図）。

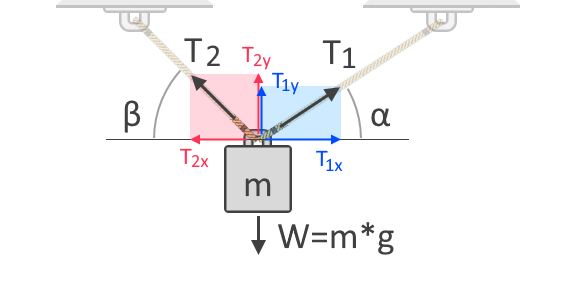
上の自由胴体図では、引張力の水平成分T₁と垂直成分T₂を見ることができます。 力はベクトルなので、常に大きさと方向を持っています。 他のベクトルと同様に、力もこれらの成分で表すことができ、それによって力の水平軸と垂直軸に沿った影響力が得られます。 T₁ₓとT₂ₓは、それぞれT₁とT₂の垂直成分です。 一方，T₁ᵧとT₂ᵧは，それぞれ同じ力の垂直成分である。

ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)
W = T₁ᵧ + T₂ᵧ

引張力の角度もわかっているので、三角関数を用いて、T₁ᵧとT₂ᵧをそれぞれT₁とT₂で表すことができます。

T₂ᵧ = T₂ * sin(β)
W = T₁ * sin(α) + T₂ * sin(β)

また、系が平衡状態にあるためには、物体が水平方向やX軸方向に移動しないことが必要だと言えます。 そのため、T₁とT₂の水平成分はゼロにならなければなりません。 また、三角法の助けを借りれば、T₁ₓとT₂ₓをそれぞれT₁とT₂で表すことができる。

T₁ₓ = T₂ₓ
T₁ * cos(α) = T₂ * cos(β)

両辺をcos(α)で割ると、T₁がT₂と角度で表される式が得られます。

T₁ = T₂ * cos(β) / cos(α)

この式を使って、以下のように力の総和の式のT₁としてT₂ * cos(β) / cos(α)を代入することで、T₂を解くことができます。

W = T₁ * sin(α) + T₂ * sin(β)
W = T₂ * * sin(α) + T₂ * sin(β)
W = T₂ *
T₂ = W /

最後に。 T₁の値をT₂で導き出したように、この式全体にcos(β) / cos(α)をかけて、すべてを簡略化すると、このような式になります。

T₁ = W / *
T₁ = W / *
T₁ = W /

あとは、テンションロープの水平に対する角度がわかればよいのです。 垂直からの角度が与えられている場合は、その角度を90°から引きます。 そうすれば、水平方向からの角度がわかります。 しかし、90°や180°よりも大きな角度が与えられた場合は、基準角度計算機を使って必要な角度を求めることができます。 引張り力の公式で変数の値を決定した後、引張り力を解くことができます

。