グラフから指数関数を求める – 指数関数
指数関数とは
指数関数の扱いや指数関数のグラフ化に入る前に、まずは指数関数の一般的な公式や理論を見てみましょう。
以下は、指数関数のグラフの最も一般的な形の1つです。

このグラフに対する指数関数の式はy=2xy=2^xy=2x, となり、最もシンプルな指数関数のグラフになります。 y=1xy=1^xy=1xがどのように見えるのか気になる方は、その指数関数グラフをご覧ください。
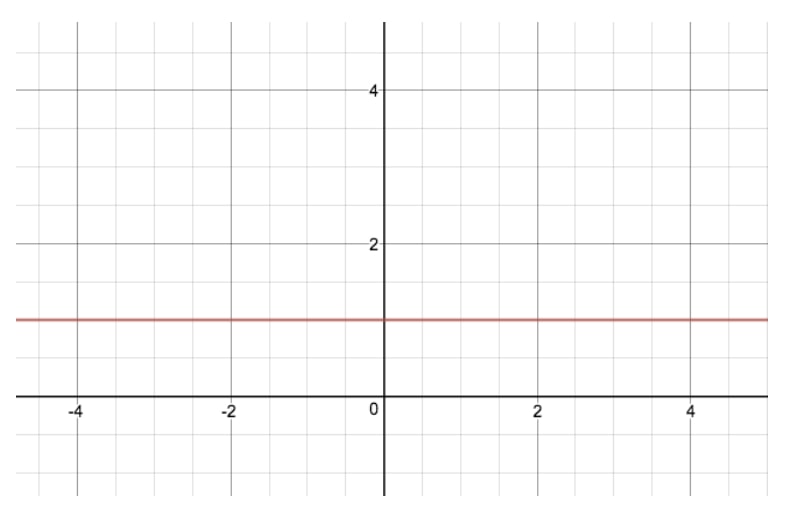
さて。 y=2xy=2^xy=2xとy=1xy=1^xy=1xのグラフがなぜこんなに違うのかということですが、指数関数の理論を理解するには、いくつかの表を見てみるのが一番です。

上の図は、1、2、3という3つの異なる「基本値」に対する3つの表です。 これらはすべて x の累乗です。 ご覧のように、「基本値」が 1 の指数関数では、1 の何乗も 1 であるため、y の値は 1 で一定です。これが、上記の y=1xy=1^xy=1x のグラフが単なる直線である理由です。 一方、y=2xy=2^xy=2xやy=3xy=3^xy=3x(写真なし)の場合は、グラフの曲線がどんどん急になっていきます。 これは、xが増加するにつれて、yの値が毎回どんどん大きな値に増加していく、いわゆる「指数関数的」に増加していくからです。
指数関数の一般的な公式を説明します。
y=abd(x-c)+ky=ab^{d(x-c)}+ky=abd(x-c)+k
上記の公式は、これまで扱ってきた関数よりも少し複雑なので、すべての変数を定義しましょう。
y – Y軸上の値
a – 垂直方向の伸縮係数
b – 基本値
x – X軸上の値
c – 水平方向の移動係数
d – 水平方向の伸縮係数
k – 垂直方向の移動係数
このレッスンでは、ごく限られた範囲でしか説明しません。 このレッスンでは、非常に基本的な指数関数についてのみ説明しますので、上記の変数のいくつかについては心配する必要はありません。 しかし、指数関数と指数関数のグラフの描き方について必要なすべての情報にアクセスできるように、これらの変数のそれぞれを変更すると指数方程式のグラフに何が起こるかを概説しましょう。
1) 変数 a
y=2xy=2^xy=2x のグラフを、a を変更した別の指数方程式と比較してみましょう。 y=(-4)2xy=(-)4)2^xy=(-4)2x

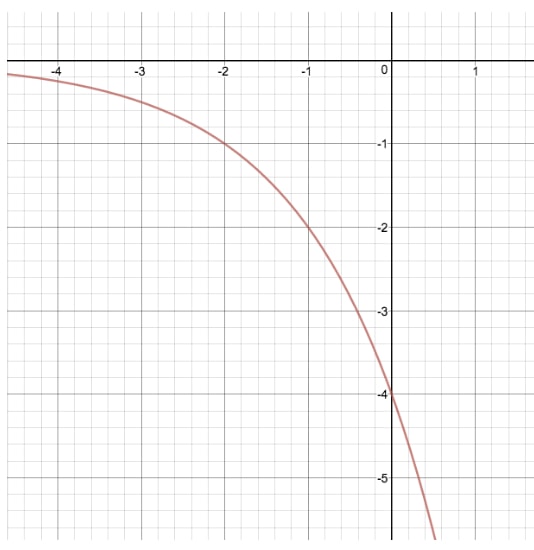
この変換を行うことで、「引き伸ばし」と「引き下げ」の両方を行うことができます。 この変換により、y=2xy=2^xy=2xの元のグラフをy値で「引き伸ばし」、「反射」したことになります。
2)変数 “b”
別名 “基本値 “とも呼ばれ、単純に指数の付いた数です。 これを求めるには、後述する代数学が必要です。
変数 “c”
y=2xy=2^xy=2xのグラフを、”c “を修正した別の指数方程式と比較してみましょう。 y=2(x-2)y=2^{(x-)2)}y=2(x-2)

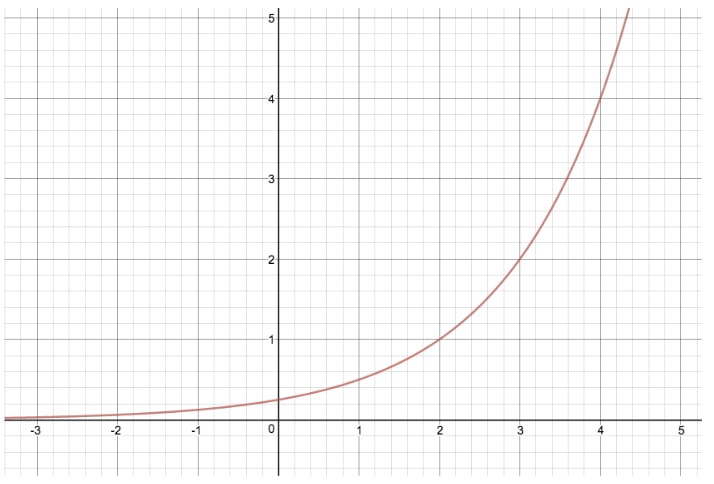
この変換を行うことで、グラフ全体を この変換により、グラフ全体を右に2単位ずらしたことになります。 もし「c」が「-2」であれば、グラフ全体を左に2単位移動させたことになります。
変数 “d”
y=2xy=2^xy=2xのグラフを、”d “を修正した別の指数方程式と比較してみましょう。 y=24xy=2^{4x}y=24x

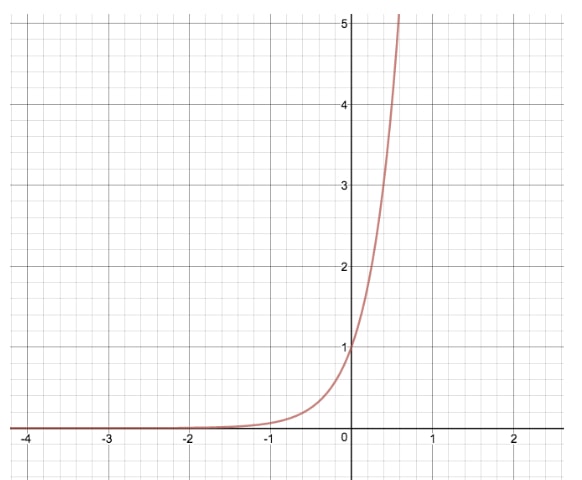
この変換を行うことで、元のグラフを伸ばすことができます。 この変換により、変数「a」がy値によって関数を修正するのと同様に、y=2xy=2^xy=2xの元のグラフをx値によって引き伸ばしています。 この例で「d」が負であれば、指数関数は、「a」で見られる垂直方向の反射ではなく、水平方向の反射を受けることになります。
変数 “k”
y=2xy=2^xy=2xのグラフを、”k “を変更した別の指数方程式と比較してみましょう。 y=2x+2y=2^x+2y=2x+2

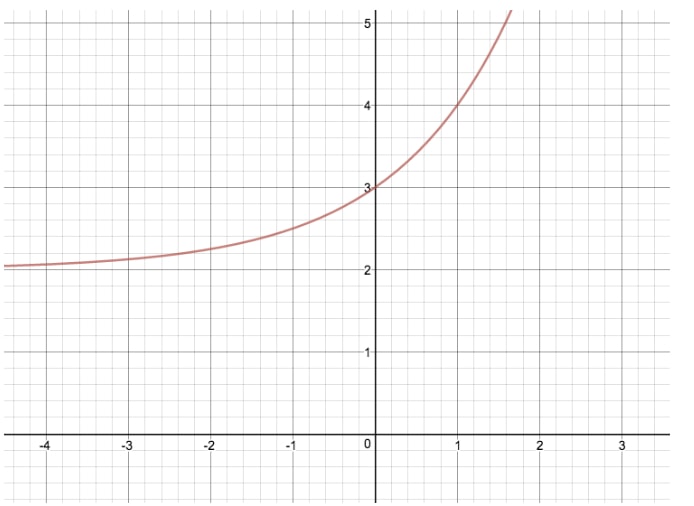
この変換を行うことで、元のyのグラフを変換することができます。 y=2xy=2^xy=2xの元のグラフを2単位上に変換したことになります。 この例で「k」が負であれば、指数関数は2単位下に変換されたことになります。 “k “は特に重要な変数で、水平漸近線と呼ばれるものにも等しいからです。 漸近線とは、関数が近づくが、実際には等しくならない x または y の値のことです。
例えば、y=2xy=2^xy=2x という関数を考えてみましょう。この指数関数では、k=0 であり、したがって、「水平漸近線」は 0 になります。 もう一つの関数y=2x+2y=2^x+2y=2x+2では、k=2なので、水平漸近線は2になります。 y=2 にするために使用できる x の値はありません。
そして、これですべての変数が揃いました。 繰り返しになりますが、これらのうちのいくつかは他のものよりも複雑なので、すべての変数を扱い、それらを見つけることに慣れるまでには時間がかかります。 指数関数をより深く理解し、上記の一般的な方程式に慣れるためには、この優れたグラフ電卓のウェブサイトをご覧ください。
さて、本題に入りましょう。
How To Find Exponential Functions
指数関数の方程式を求めるには複数のステップが必要で、与えられた情報やグラフの種類によって問題はそれぞれ異なります。 指数関数のグラフが与えられた場合、グラフ自体からいくつかの情報を得て、グラフから直接得ることができないものを解くことができる必要があります。 以下は、私たちが探さなければならないすべての変数と、それらを通常どのようにして見つけるかのリストです。
a – 代数を使って解くか、与えられる
b – 代数を使って解くか、与えられる
c – x = 0とし、”c “が存在しないと想像すると、yの値はy切片と同じになります。 yの値はy切片と同じになります。y切片のyの値がy軸から何単位離れているかを数えると、これは「c」と同じになります
d – 代数を使って解きます
k – 水平漸近線の値と同じになります
もちろん、これらは指数関数の方程式を求めるために必要な一般的な手順にすぎません。
指数関数の例:
では、これまで説明してきた理論を実践するために、いくつかの例を挙げてみましょう。 練習すれば、簡単に指数関数を見つけられるようになりますよ!
例題1:
与えられたグラフのy=abxy=ab^xy=abxの形の指数関数を求めなさい。
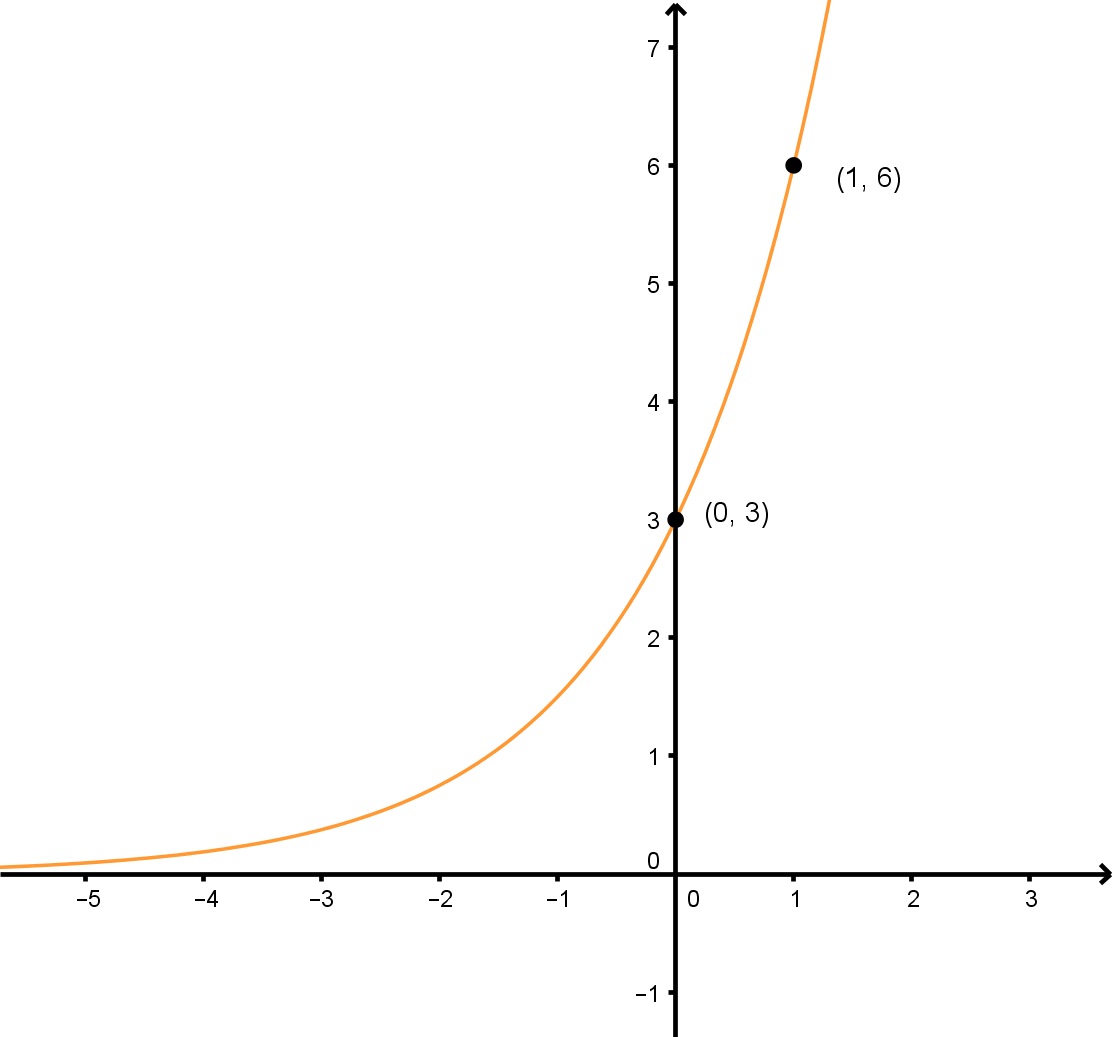
この問題を解くには、変数 “a “と “b “を求める必要があります。
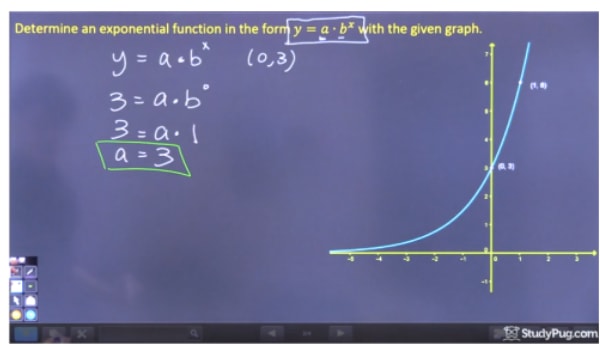
Step 1: Solve for “a”
「a」を解くためには、bxを消去できるグラフ上の点を選ばなければなりません。 b0は1に等しいので、a=3と求めることができます。 近道としては、kの値がないので、aはこの方程式のy切片と同じになります。
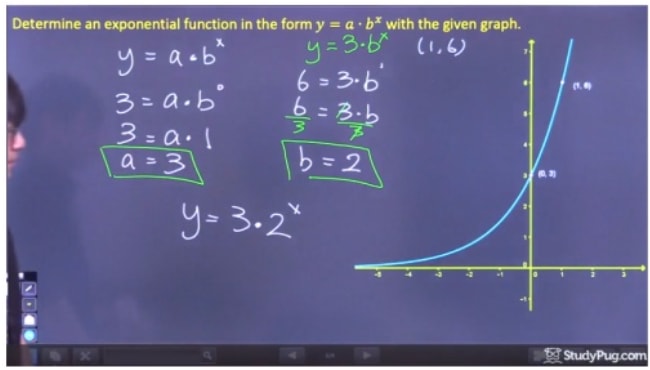
ステップ2: bを解く
ステップ3: 最終的な方程式を書く
例題2:
与えられたグラフのy=a2dx+ky=a2^{dx}+ky=a2dx+kの形の指数関数を求めよ。
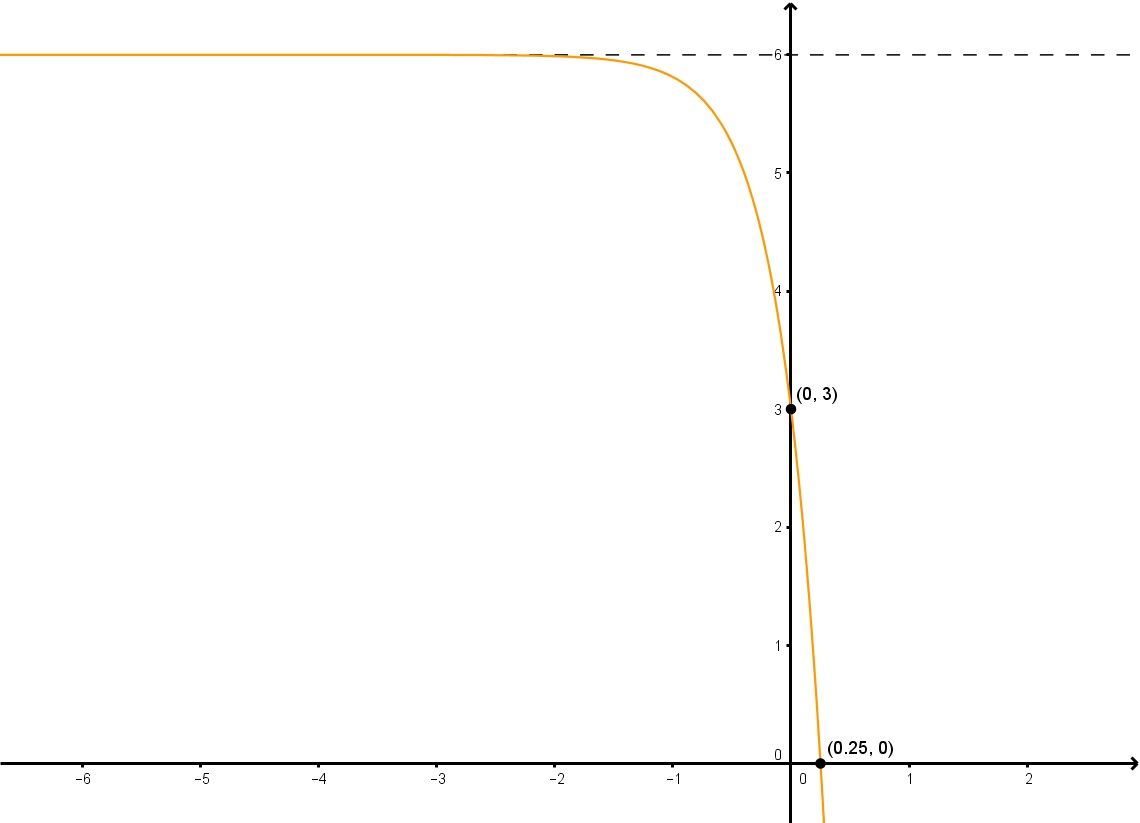
ステップ1: グラフから「k」を求める
「k」を求めるために必要なのは、水平漸近線を見つけることで、それは明らかにy=6です。 したがって、k=6となります。
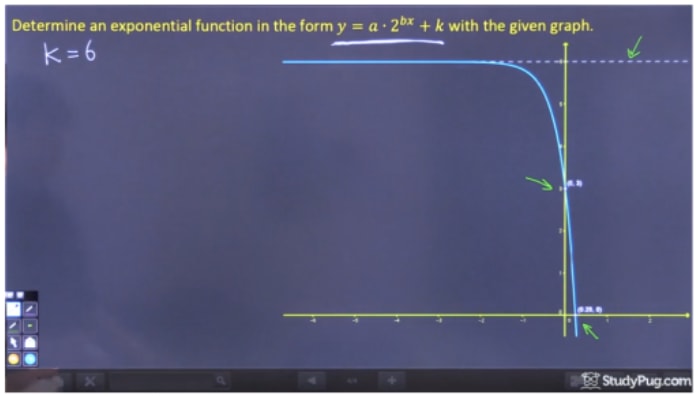
ステップ2: a “を解く
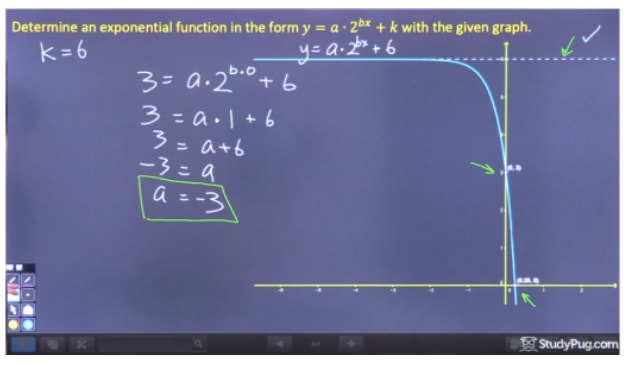
ステップ3: bを解く

ステップ4: 最終的な方程式を書く

以上で指数関数の説明は終わりです。 繰り返しになりますが、これらの関数は直線や放物線の方程式よりも少し複雑なので、たくさんの練習問題を解いて、新しい変数やテクニックのコツをつかむようにしてください。 練習を重ねれば、すぐに指数方程式や指数関数のグラフも問題なく描けるようになります!