マトリックスインバージョン。 行列の逆行列を求める
レッスンインデックスに戻る|レッスンを順番にこなす|印刷用ページ
行列の逆行列。
行列の逆数を求める (1/2ページ)
行列には、割り算というものがありません。 行列の足し算、引き算、掛け算はできますが、割り算はできません。 しかし、関連する概念として「反転」と呼ばれるものがあります。
最初に連立方程式の解き方を学んだときのことを思い出してください。 3x = 6」のような問題が与えられた場合、両辺を3で割って解きます。1/3を掛けることは3で割ることと同じなので、両辺に1/3を掛けてもx = 2という同じ答えが得られます。「(3/2)x = 6」のような問題を解く必要がある場合、両辺を3/2で割ることもできますが、両辺に2/3を掛ける方が簡単でしょう。 2/3という逆数は、3/2の逆数であり、2つの分数を掛け合わせると1になることから、この文脈では「(乗法)恒等式」と呼ばれています。
Advertisement
この用語と事実は、行列にとって非常に重要です。 AX = Cのような行列式で、AとCが与えられ、Xを求めよと言われたら、行列Aを「割り算」したいと思います。 しかし、行列では割り算はできません。 一方、上記の逆数を求めるのと同じように、Aの逆数を求めることができればどうでしょうか。
AX = C
A-1AX = A-1C
IX = A-1C
X = A-1C
式の左辺の「A-1AX」がどのようにして「X」になったのでしょうか? 普通の数の逆数の性質を思い出してみてください。 ある数字(3/2など)とその逆数(この場合は2/3)があって、それを掛け合わせると1になります。 1は恒等式で、任意の数xに対して1x=xであることからそう呼ばれています。 ある行列(Aなど)とその逆行列(この場合は
A-1)を掛け合わせると、恒等行列Iになります。
注意すべきは、上記の乗算における順序は重要であり、全く任意ではないということです。 行列の場合、乗算は可換ではないことを思い出してください。 つまり、ABとBAが等しくなることはほとんどありません。 つまり、行列式を「左に」掛けて(A-1AXを得る)も、「右に」掛けて(AXA-1を得る)も、全く同じではないのです。 そして、積のAXA-1がA-1AXに等しいとは言えません。なぜなら、乗算の順序を入れ替えることはできないからです。 代わりに、A-1を左に掛けて、元の行列式のAのすぐ隣に置かなければなりません。 そして、解くときには方程式の両辺に同じことをしなければならないので、方程式の右辺にも「左」をかけなければならず、A-1Cとなります。 このように、行列の配置は気軽にできるものではなく、正確に、正しく、一貫して行わなければなりません。
以上のように、逆行列は行列式を解くのに非常に役立ちます。 しかし、行列が与えられたとき、それをどのように反転させるのでしょうか? どうやって逆行列を見つけるのでしょうか? 行列を反転させるテクニックは、ちょっとした工夫が必要です。 与えられた行列Aとその逆行列A-1に対して、A-1A = Iがあることがわかっています。
- 次の行列の逆行列を求めなさい。
![]](https://www.purplemath.com/modules/matrices/invers01.gif)
まず、行列Aのエントリーを書きますが、2倍幅の行列で書きます。
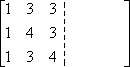
ダブルワイドのもう半分には、恒等行 列を書きます。
![]](https://www.purplemath.com/modules/matrices/invers05.gif)
さて、ダブルワイドの左辺を恒等式に変換するために、行列の行操作を行います。 (行操作の常として、これを行うための唯一の「正しい」方法はありません。 以下の手順は、たまたま私が思いついたものです。

さて、ダブルワイドの左辺には恒等式が含まれており、右辺には逆行列が含まれています。 つまり、逆行列は次のようになります:
![]](https://www.purplemath.com/modules/matrices/invers04.gif)
なお、この行列がAの逆行列であることを確認するには、2つの行列を掛け合わせて恒等式が得られることを確認すればよいことになります。 Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved

「実生活」では、逆行列がこのようにきれいな整数で埋め尽くされた行列であることはほとんどないことをご承知おきください。 しかし、運が良ければ、特に逆行列を手作業で行っている場合は、このような素晴らしいものが与えられるでしょう。
Top|1|2|Return to Index Next >>
|
Cite this article as: |
Stapel, Elizabeth. “Matrix Inversion: Find the Inverse of a Matrix.” Purplemath. Available from 2016
|