階乗
階乗とは
ある正の数または整数(nで表す)の階乗(n!と表す)は、n(正の整数)に先行するまたは等価なすべての正の数の積である。
1200年代に入り、順列を数えるために階乗が使われるようになりました。
1200年代から階乗は順列を数えるために使われていましたが、1800年代初頭にフランスの数学者Christian Krampによって階乗の表記法(n!と表記される)は、n(正の整数)に先行する、あるいはnに相当するすべての正の数の積である。
1以上の値や整数を見た場合、次のように書くことができます。
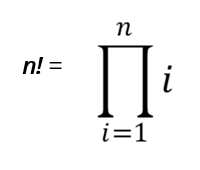
上の式をπ積の表記法に従って書くと、次のような繰り返しの関係になります。 = n ∙ (n – 1) !
この表記法の例を以下に示します。
階乗表
以下の表は0から10までの整数の階乗の概要を示したものです。
0!=1
上記のような表記や定義を正当化する理由はいくつかあります。
また、n = 0 の場合、その階乗 (n!) の定義は、数のない積を包含し、より広い意味で乗法恒等式と同等であることを意味します。
Definitions to Note in Relation to the Zero Factorial
- Combinatorics (組合せ論)。
- 順列。
- Permutation(順列):数学では、集合のメンバーを直線的な順序や順番に並べることを指します。
Recurrence relation: 数学では、再帰的に一連の、あるいは膨大な数の値を定義する方程式を指します。
階乗関数のさまざまな応用
階乗関数は、数学のさまざまな分野で見られます。 まず、n個の特定の物体を順番に並べるには、n!個の区別された方法があります。
階乗は、代数学では二項定理、微積分学ではテイラーの式の分母にも現れます。
その他の階乗に類似した数列
数学には階乗に類似した数列がいくつかあります。
- 二重階乗(三角関数の積分を簡単にするために使用される)
- 多階乗(複数の感嘆符で表すことができる)
- 初階乗(n以下の素数の積を得ることになる)。
- 超階乗:最初の n 階乗の積として定義されます。
- 超階乗:1 から n までの連続した値の数を乗算した結果です。
追加リソース
CFIは、グローバルなCommercial Banking & Credit Analyst (CBCA)™認定の公式プロバイダーですCommercial Banking & Credit Analyst (CBCA)™認定は、ファイナンスをカバーするクレジットアナリストのグローバルスタンダードです。 CBCAは、財務、会計、信用分析、キャッシュフロー分析、コベナンツ・モデリング、ローン返済などをカバーするクレジット・アナリストの世界基準です。 の認定プログラムで、誰もが世界レベルの財務アナリストになれるように設計されています。
- Correlation Matrix相関行列相関行列とは、簡単に言えば、異なる変数の相関係数を表示した表です。 相関行列は、表の中のすべての可能な値のペアの間の相関を表します。
- Financial Mathematics金融数学金融数学は、金融問題を解決するための数学および数学的モデリングの応用について説明します。
- QuantsQuantitative Analyst(「クォンツ」とも呼ばれる)は、複雑な金融問題を解決するためのアルゴリズムおよび数学的または統計的モデルの設計、開発、および実装を専門とするプロフェッショナルです。
- Standard DistributionSampling Distributionサンプリング分布とは、与えられた母集団から無作為にサンプルを選んだときに得られる統計量の確率分布のことです。