Matrix-Inversion: Finden der Inversen einer Matrix

Zurück zum Lektionsindex | Lektionen der Reihe nach bearbeiten | Druckfreundliche Seite

Matrixinversion:
Finden der Inversen einer Matrix (Seite 1 von 2)

Für Matrizen gibt es keine Division. Man kann Matrizen addieren, subtrahieren und multiplizieren, aber man kann sie nicht dividieren. Es gibt jedoch ein verwandtes Konzept, das „Inversion“ genannt wird. Zuerst werde ich erörtern, warum die Inversion nützlich ist, und dann zeige ich Ihnen, wie man sie durchführt.

Erinnern Sie sich an die Zeit zurück, als Sie zum ersten Mal lernten, wie man lineare Gleichungen löst. Wenn Sie etwas wie „3x = 6“ erhielten, würden Sie die Aufgabe lösen, indem Sie beide Seiten durch 3 dividieren. Da die Multiplikation mit 1/3 dasselbe ist wie die Division durch 3, könnten Sie auch beide Seiten mit 1/3 multiplizieren, um dieselbe Antwort zu erhalten: x = 2. Wenn Sie etwas wie „(3/2)x = 6“ lösen müssten, könnten Sie immer noch beide Seiten durch 3/2 dividieren, aber es war wahrscheinlich einfacher, beide Seiten mit 2/3 zu multiplizieren. Der reziproke Bruch 2/3 ist der Kehrwert von 3/2, denn wenn Sie die beiden Brüche multiplizieren, erhalten Sie 1, was in diesem Zusammenhang „die (multiplikative) Identität“ genannt wird: 1 wird die Identität genannt, weil die Multiplikation von etwas mit 1 seinen Wert nicht ändert.

Diese Terminologie und diese Fakten sind für Matrizen sehr wichtig. Wenn Sie eine Matrixgleichung wie AX = C erhalten, bei der Ihnen A und C gegeben sind und Sie X herausfinden sollen, würden Sie gerne die Matrix A „abdividieren“. Aber Sie können keine Division mit Matrizen durchführen. Was wäre aber, wenn man den Kehrwert von A finden könnte, ähnlich wie beim Finden des reziproken Bruchs oben? Die Inverse von A, geschrieben als „A-1“ und ausgesprochen als „A invers“, würde es Ihnen ermöglichen, das A aus der Matrixgleichung zu streichen und dann für X zu lösen.

AX = C
A-1AX = A-1C
IX = A-1C
X = A-1C

Wie wurde „A-1AX“ auf der linken Seite der Gleichung zu „X“? Denken Sie zurück an die Natur der Inversen für reguläre Zahlen. Wenn Sie eine Zahl (z. B. 3/2) und ihre Umkehrung (in diesem Fall 2/3) haben und diese multiplizieren, erhalten Sie 1. Und 1 ist die Identität, so genannt, weil 1x = x für jede beliebige Zahl x. Genauso funktioniert es bei Matrizen. Multipliziert man eine Matrix (z. B. A) und ihre Inverse (in diesem Fall
A-1), erhält man die Identitätsmatrix I. Und die Pointe der Identitätsmatrix ist, dass IX = X für jede beliebige Matrix X (gemeint ist natürlich „jede Matrix der richtigen Größe“) ist.

Es sei angemerkt, dass die Reihenfolge bei der obigen Multiplikation wichtig ist und keineswegs beliebig ist. Erinnern Sie sich, dass die Multiplikation für Matrizen nicht kommutativ ist. Das heißt, AB ist fast nie gleich BA. Die Matrixgleichung „links“ zu multiplizieren (um A-1AX zu erhalten) ist also ganz und gar nicht dasselbe wie „rechts“ zu multiplizieren (um AXA-1 zu erhalten). Und Sie können nicht sagen, dass das Produkt AXA-1 gleich A-1AX ist, weil Sie die Reihenfolge bei der Multiplikation nicht umdrehen können. Stattdessen müssen Sie A-1 auf der linken Seite multiplizieren, also direkt neben dem A in der ursprünglichen Matrixgleichung. Und da Sie beim Lösen einer Gleichung auf beiden Seiten dasselbe tun müssen, müssen Sie auch auf der rechten Seite der Gleichung „links“ multiplizieren, was zu A-1C führt. Sie können nicht zufällig mit Ihrer Platzierung der Matrizen sein; Sie müssen präzise, korrekt und konsistent sein. Nur so können Sie A erfolgreich aufheben und die Matrixgleichung lösen.

Wie Sie oben gesehen haben, können inverse Matrizen sehr nützlich für die Lösung von Matrixgleichungen sein. Aber wie invertiert man eine gegebene Matrix? Wie findet man die Inverse? Die Technik zum Invertieren von Matrizen ist ziemlich clever. Für eine gegebene Matrix A und ihre Inverse A-1 wissen wir, dass wir A-1A = I haben. Wir werden die Identitätsmatrix I im Verfahren zum Invertieren einer Matrix verwenden.

• Finden Sie die Inverse der folgenden Matrix.

Zunächst schreibe ich die Einträge der Matrix A auf, aber ich schreibe sie in eine doppelt breite Matrix:

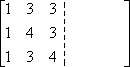
In die andere Hälfte der doppelt breiten Matrix schreibe ich die Identitätsmatrix:

Nun führe ich Matrix-Zeilenoperationen durch, um die linke Seite der doppelten Breite in die Identität zu verwandeln. (Wie immer bei Zeilenoperationen gibt es nicht den einen „richtigen“ Weg, dies zu tun. Was folgt, sind nur die Schritte, die mir zufällig in den Sinn kamen. Ihre Berechnungen könnten leicht ganz anders aussehen.)

Nun, da die linke Seite der doppelten Breite die Identität enthält, enthält die rechte Seite die Inverse. Das heißt, die inverse Matrix ist die folgende:

Beachten Sie, dass wir bestätigen können, dass diese Matrix die Inverse von A ist, indem wir die beiden Matrizen multiplizieren und bestätigen, dass wir die Identität erhalten: Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved

Bitte beachten Sie, dass im „wirklichen Leben“ die Inverse selten eine Matrix ist, die mit schönen, sauberen ganzen Zahlen wie dieser gefüllt ist. Mit etwas Glück, vor allem wenn Sie Inversen von Hand machen, bekommen Sie aber schöne wie diese zu tun.

Top | 1 | 2 | Zurück zum Index Weiter >>