10.2 – Autocorrelatie en tijdreeksenmethoden
Een veel voorkomende manier waarop de “onafhankelijkheids”-voorwaarde in een meervoudig lineair regressiemodel faalt, is wanneer de steekproefgegevens in de loop van de tijd zijn verzameld en het regressiemodel er niet in slaagt om eventuele tijdstrends effectief te vatten. In een dergelijke situatie zijn de toevallige fouten in het model vaak positief gecorreleerd in de tijd, zodat elke toevallige fout meer gelijkenis vertoont met de vorige toevallige fout dan het geval zou zijn indien de toevallige fouten onafhankelijk van elkaar waren. Dit verschijnsel staat bekend als autocorrelatie (of seriële correlatie) en kan soms worden opgespoord door de modelresiduen uit te zetten tegen de tijd. Wij zullen dit in dit en het volgende hoofdstuk nader onderzoeken.
Een tijdreeks is een opeenvolging van metingen van dezelfde variabele(n) in de tijd. Gewoonlijk worden de metingen op gelijkmatig verdeelde tijdstippen verricht – bijvoorbeeld maandelijks of jaarlijks. Laten we eerst het probleem bekijken waarin we een y-variabele hebben die als een tijdreeks wordt gemeten. Als voorbeeld kan y een maat zijn voor de temperatuur op aarde, met metingen die elk jaar worden waargenomen. Om te benadrukken dat wij gemeten waarden in de tijd hebben, gebruiken wij “t” als subscript in plaats van de gebruikelijke “i”, d.w.z., \(y_t) betekent \(y) gemeten in de tijdsperiode \(t). Van een autoregressiemodel is sprake wanneer een waarde uit een tijdreeks wordt geregresseerd op eerdere waarden uit diezelfde tijdreeks. bijvoorbeeld \(y_{t}) op \(y_{t-1}):
In dit regressiemodel is de responsvariabele in de vorige tijdperiode de voorspeller geworden en de fouten hebben onze gebruikelijke aannames over fouten in een eenvoudig lineair regressiemodel. De volgorde van een autoregressie is het aantal onmiddellijk voorafgaande waarden in de reeks die worden gebruikt om de waarde op het huidige tijdstip te voorspellen. Het voorgaande model is dus een eerste-orde autoregressie, geschreven als AR(1).
Als we dit jaar \(y_{t}) willen voorspellen aan de hand van metingen van de mondiale temperatuur in de voorgaande twee jaar (\(y_{t-1},y_{t-2})), dan zou het autoregressieve model daarvoor zijn:
Dit model is een tweede-orde autoregressie, geschreven als AR(2), omdat de waarde op tijdstip $t$ wordt voorspeld uit de waarden op de tijdstippen \(t-1) en \(t-2). Meer algemeen is een autoregressie van de orde ^(k^textrm{e}}, geschreven als AR(k), een meervoudige lineaire regressie waarin de waarde van de reeks op elk tijdstip t een (lineaire) functie is van de waarden op de tijdstippen \(t-1,t-2,\ldots,t-k\).
Autocorrelatie en partiële autocorrelatie
De correlatiecoëfficiënt tussen twee waarden in een tijdreeks wordt de autocorrelatiefunctie (ACF) genoemd. Bijvoorbeeld de ACF voor een tijdreeks \(y_t\) wordt gegeven door:
De waarde van k is het beschouwde tijdsverschil en wordt de lag genoemd. Een lag 1 autocorrelatie (d.w.z. k = 1 in het bovenstaande) is de correlatie tussen waarden die één tijdvak uit elkaar liggen. Meer in het algemeen is een lag k autocorrelatie de correlatie tussen waarden die k tijdsperioden uit elkaar liggen.
De ACF is een manier om het lineaire verband te meten tussen een waarneming op tijdstip t en de waarnemingen op eerdere tijdstippen. Als we uitgaan van een AR(k) model, dan willen we misschien alleen het verband meten tussen y_{t} en y_{t-k} en de lineaire invloed uitfilteren van de willekeurige variabelen die daartussen liggen (d.w.z. y_{t-1},y_{t-2},y_{t-(k-1 )}), waarvoor een transformatie van de tijdreeksen nodig is. Door vervolgens de correlatie van de getransformeerde tijdreeksen te berekenen, verkrijgen we de partiële autocorrelatiefunctie (PACF).
De PACF is het nuttigst om de volgorde van een autoregressief model te bepalen. Meer in het bijzonder duiden partiële autocorrelaties die significant verschillen van 0 op vertraagde termen van y die bruikbare voorspellers zijn van y. Het is belangrijk dat de keuze van de volgorde zinvol is. Stel bijvoorbeeld dat u bloeddrukmetingen hebt van elke dag in de afgelopen twee jaar. Misschien vindt u dat een AR(1) of AR(2) model geschikt is om de bloeddruk te modelleren. De PACF kan echter een grote partiële autocorrelatie aangeven bij een lag van 17, maar zo’n grote orde voor een autoregressief model heeft waarschijnlijk niet veel zin.
Voorbeeld 1: Google Data
De dataset (google_stock.txt) bestaat uit n = 105 waarden die de slotkoers zijn van een aandeel Google gedurende 2-7-2005 tot 7-7-2005. We zullen de dataset analyseren om de volgorde van een autoregressief model te bepalen. Een plot van de aandelenkoersen versus tijd wordt in de onderstaande figuur gepresenteerd:
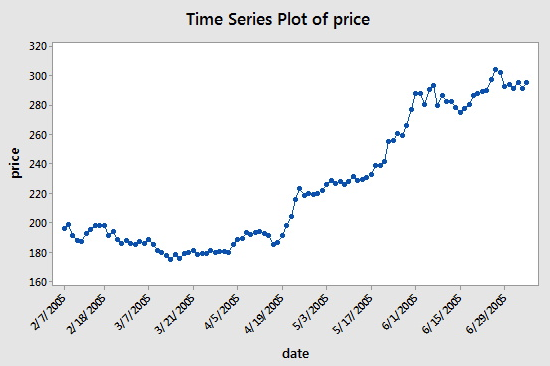
De opeenvolgende waarden lijken elkaar vrij dicht op te volgen, wat suggereert dat een autoregressiemodel geschikt zou kunnen zijn. Vervolgens bekijken we een plot van gedeeltelijke autocorrelaties voor de gegevens:
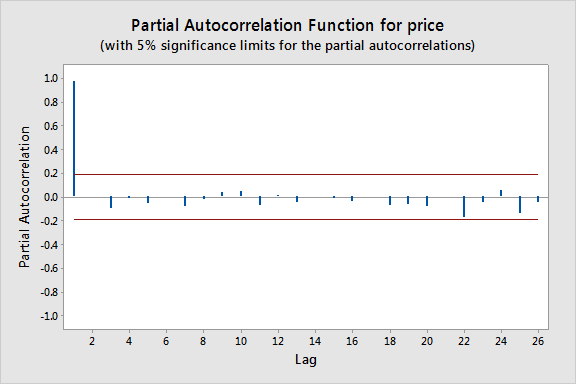
Hier zien we dat er een significante piek is bij een lag van 1 en veel lagere pieken voor de volgende lags.
Er kunnen voor deze plot ook benaderende grenzen worden geconstrueerd (zoals gegeven door de rode lijnen in de plot hierboven) om te helpen bij het bepalen van grote waarden. Benaderende significantiegrenzen worden gegeven door significantiegrenzen van z_{1-alfa/2}/qrt{n}). Waarden die buiten een van deze grenzen liggen zijn een aanwijzing voor een autoregressief proces.
We creëren nu een lag-1 prijsvariabele en bekijken een scatterplot van prijs versus deze lag-1 variabele:
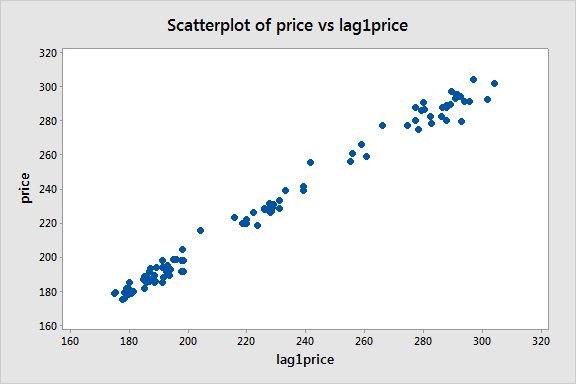
Er blijkt een sterk lineair patroon te zijn, dat bevestigt dat het eerste-orde autoregressiemodel
bruikbaar zou kunnen zijn.
Voorbeeld 2: Gegevens over aardbevingen
Laat yt = het jaarlijkse aantal wereldwijde aardbevingen met een magnitude van meer dan 7 op de schaal van Richter voor n = 100 jaar (earthquakes.txt gegevens verkregen uit https://earthquake.usgs.gov). Onderstaande plot geeft een tijdreeksplot voor deze dataset.
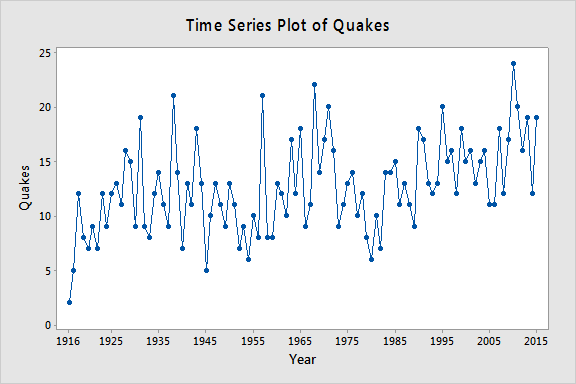
Het onderstaande plot geeft een plot van de PACF (partiële autocorrelatiefunctie), die zo kan worden geïnterpreteerd dat een autoregressie van de derde orde gerechtvaardigd kan zijn, aangezien er opmerkelijke partiële autocorrelaties voor lags 1 en 3 zijn.
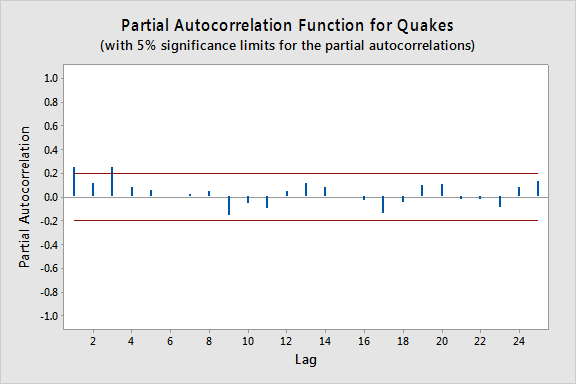
De volgende stap is het uitvoeren van een meervoudige lineaire regressie met het aantal bevingen als de responsvariabele en lag-1, lag-2 en lag-3 bevingen als de voorspellende variabelen. In de resultaten hieronder zien we dat de lag-3 voorspeller significant is op het 0,05-niveau (en de p-waarde van de lag-1 voorspeller is ook relatief klein).