3.7 – Power Analysis

Na afloop van een statistische test worden conclusies getrokken over de nulhypothese. In gevallen waarin de nulhypothese niet wordt verworpen, kan een onderzoeker nog steeds van mening zijn dat de behandeling wel degelijk een effect heeft gehad. Laten we zeggen dat er drie behandelingen voor gewichtsverlies zijn uitgevoerd. Aan het einde van de studie analyseert de onderzoeker de gegevens en stelt vast dat er geen verschillen zijn tussen de behandelingen. De onderzoeker gelooft dat er wel degelijk verschillen zijn. Hoewel je zou kunnen denken dat dit slechts wishful thinking van de kant van de onderzoeker is, kan er een statistische reden zijn voor het gebrek aan significante bevindingen.

Op dit punt kan de onderzoeker een poweranalyse uitvoeren. U herinnert zich uit uw inleidende tekst of cursus dat power het vermogen is om de nul te verwerpen wanneer de nul werkelijk onjuist is. De factoren die van invloed zijn op de power zijn de steekproefgrootte (grotere steekproeven leiden tot meer power), de effectgrootte (behandelingen die resulteren in grotere verschillen tussen groepen zullen verschillen hebben die sneller worden gevonden), de variabiliteit van het experiment, en de significantie van de type 1 fout.

Opgemerkt moet worden dat de meest gangbare poweranalyses die zijn welke de benodigde steekproefgroottes voor experimentele ontwerpen berekenen. Bij deze analyses wordt gebruik gemaakt van proefgegevens of eerder onderzoek. Wanneer een power analyse van tevoren wordt gemaakt, is er sprake van een PROSPECTIVE power analyse. In ons voorbeeld is het gebruik van een power analyse nadat het experiment is uitgevoerd een retrospectieve power analyse.

Dus terug naar ons voorbeeld. Normaal gesproken willen we een power van 80%. Nogmaals, de macht vertegenwoordigt ons vermogen om de nul af te wijzen wanneer deze onwaar is, dus een macht van 80% betekent dat we dit in 80% van de gevallen goed doen. Het omgekeerde betekent dat we in 20% van de gevallen het risico lopen de nul niet te verwerpen terwijl we dat eigenlijk wel zouden moeten doen.

Op basis van ons voorbeeld van de kas kunnen we een retrospectieve poweranalyse uitvoeren (ter herinnering: dit doen we meestal niet, tenzij we een reden hebben om te vermoeden dat de power van onze test erg laag was). Dit is een analyse waarbij Minitab veel eenvoudiger is en toch net zo nauwkeurig als SAS, dus we zullen Minitab gebruiken om deze eenvoudige poweranalyse te illustreren.

Minitab: Vermogensanalyse

U kunt de onderstaande schermafbeeldingen volgen om toegang te krijgen tot het menu Vermogen in Minitab.

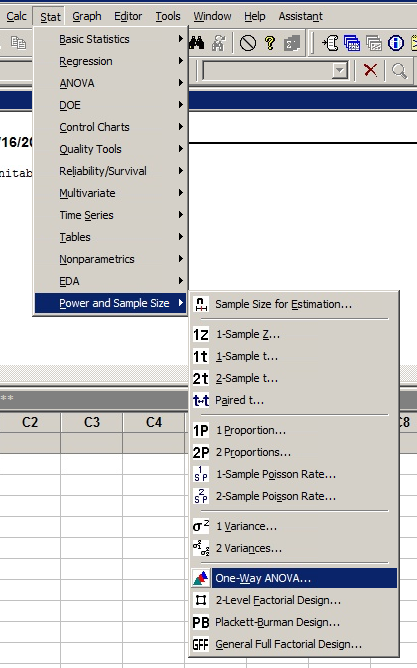
Omdat we een eenzijdige ANOVA hebben, selecteren we deze test (u ziet dat er machtsanalyses voor veel verschillende tests zijn en dat SAS nog ingewikkeldere opties toestaat)

Daarna vraagt het dialoogvenster u om de vier hierboven beschreven elementen.

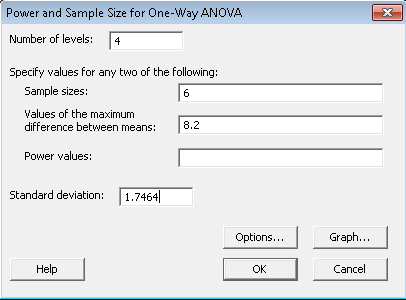
Als u naar ons ingevulde dialoogvenster kijkt, ziet u dat we geen waarde hebben ingevoerd voor power. Dit komt omdat Minitab het vak berekent dat u leeg laat (dus als we steekproefgrootte nodig hadden, zouden we steekproefgrootte leeg laten en een waarde voor power invullen. In ons voorbeeld weten we dat het aantal niveaus 4 is omdat we vier behandelingen hebben. We hebben zes waarnemingen voor elke behandeling, dus de steekproefgrootte is 6. De waarde voor het maximale verschil in de gemiddelden is 8,2 (we hebben gewoon het kleinste gemiddelde van het grootste gemiddelde afgetrokken, en de standaardafwijking is 1,747. Waar komt dit vandaan? De MSE vertegenwoordigt de fout in het model. Wij beschouwen de MSE ook als de variabiliteit in het model. Om de standaardafwijking te krijgen, nemen we gewoon de vierkantswortel van de MSE (in dit geval was de MSE ongeveer 3).

Als we op OK klikken, krijgen we de volgende uitvoer:

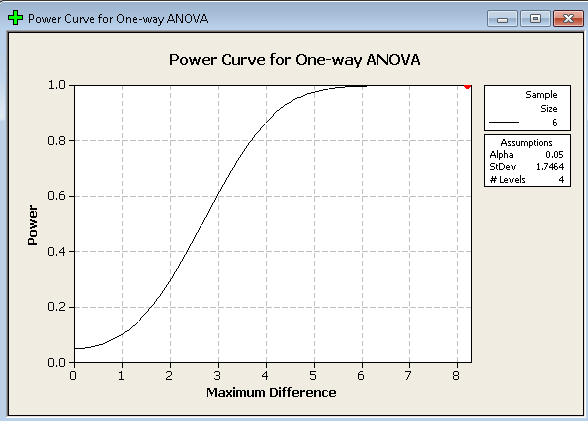
Als u deze grafiek volgt, ziet u dat de macht op de y-as staat. Aangezien we willen weten wat het vermogen van het groene huisvoorbeeld is, hoeven we alleen maar het rode bolletje op de grafiek te zoeken. Het is moeilijk te vinden, maar als je goed kijkt, komt het rode puntje overeen met een macht van 1. Dat is zeer ongebruikelijk, maar het is gemakkelijk te verklaren dat de gegevens van de kas zijn samengesteld om verschillen te laten zien.

We kunnen de vraag stellen, hoe zit het met verschillen tussen de behandelingsgroepen, de controle buiten beschouwing gelaten? We hoeven alleen maar wat invoer in Minitab aan te passen.

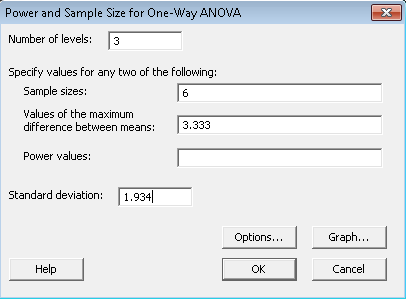
Let op de verschillen hier ten opzichte van de vorige schermafbeelding. We hebben nu 3 niveaus omdat we alleen de drie behandelingen bekijken. De maximale verschillen tussen de gemiddelden en ook de standaardafwijking zijn ook anders.

De uitvoer is nu veel gemakkelijker te zien:

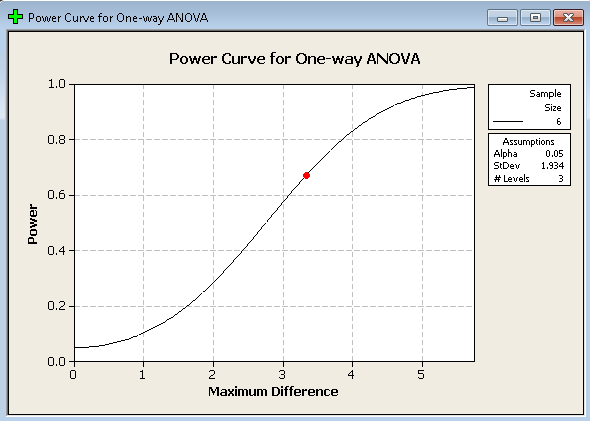
Hier zien we dat het vermogen lager is dan wanneer we de controle meerekenen. De belangrijkste reden voor deze afname is dat het verschil tussen de gemiddelden kleiner is.

U kunt experimenteren met de machtsfunctie in Minitab om u te voorzien van steekproefgroottes, enzovoort voor verschillende machten. Hieronder ziet u een voorbeeld van de uitvoer wanneer we vragen om verschillende machtscurven voor verschillende steekproefgrootten, een soort “wat als”-scenario.

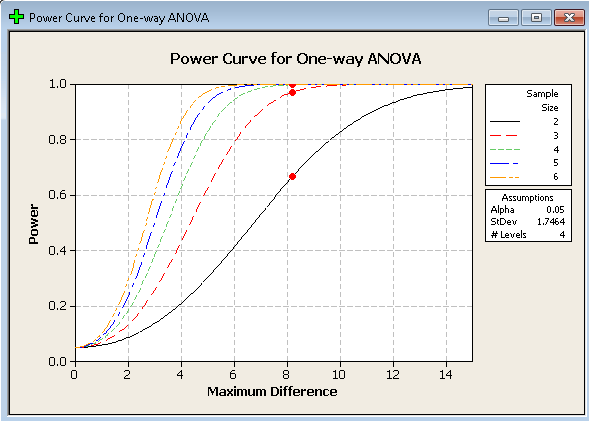
Even ter herinnering: machtsanalyses worden meestal uitgevoerd VOORDAT een experiment wordt uitgevoerd, maar af en toe kan een machtsanalyse aanwijzingen geven over de reden waarom significante verschillen niet zijn gevonden.