32-bit ALU
Bij het invoeren van numerieke waarden in de antwoordvelden kunt u gebruik maken van gehele getallen (1000, 0x3E8, 0b1111101000), floating-point getallen (1000.0), wetenschappelijke notatie (1e3), technische schaalfactoren (1K), of numerieke expressies (3*300 + 100) gebruiken.Nuttige links:
- Inleiding tot Jade
- Standaardcellenbibliotheek
Opgave 1. Design Problem: 32-bit Arithmetic and Logic UnitZie de instructies hieronder.Gebruik de Jade instance hieronder om uw ontwerp in te voeren. Om dit ontwerpprobleem te voltooien, selecteer de /alu/alu module en klik in de Jade toolbar en de ingebouwde tester zal ofwel discrepanties rapporteren tussen de verwachte en de werkelijke output, of, als je ontwerp correct is, zal het registreren dat de test geslaagd is.{ “shared_modules”: , “hierarchical”: “true”, “parts”: , “tools”: , “editors”: , “edit”: ,”/alu/alu”, “required_tests”: }In dit practicum bouwen we de rekenkundige en logische eenheid (ALU) voor de Beta processor. De ALU heeft twee 32-bit ingangen (die we “A” en “B” zullen noemen) en produceert één 32-bit uitgang. We beginnen met het ontwerp van elk onderdeel van de ALU als een afzonderlijke schakeling, die elk zijn eigen 32-bits uitgang produceert. Daarna combineren we deze uitgangen tot een enkel ALU-resultaat.Bij het ontwerpen van schakelingen zijn er drie factoren die geoptimaliseerd kunnen worden:
- ontwerp voor maximale prestaties (minimale latency)
- ontwerp voor minimale kosten (minimale oppervlakte)
- ontwerp voor de beste kosten/prestatie verhouding (minimaliseer oppervlakte*latency)
Gelukkig is het vaak mogelijk om alle drie tegelijk te doen, maar in sommige delen van de schakeling zal een soort afweging gemaakt moeten worden. Bij het ontwerpen van je schakeling moet je kiezen welke van de drie factoren het belangrijkst voor je is en je ontwerp daarop afstemmen. De standaard celbibliotheek & gate-level simulatie De bouwstenen voor dit lab komen uit een bibliotheek van logische poorten – IC-fabrikanten hebben vaak een “standaard celbibliotheek” en verschillende ontwerphulpmiddelen om het voor hun klanten gemakkelijker te maken te ontwerpen zonder zich zorgen te hoeven maken over de gedetailleerde geometrie van de maskerlagen die worden gebruikt om mosfets en bedrading te maken. 6.004 heeft zijn eigenStandard Cell Library die voorziet in:
2-, 3- en 4-input AND, OR, NAND en NOR gates
2-input XOR en XNOR gates
2:1 en 4:1 multiplexors
D-register en D-latches
Zie de bibliotheekdocumentatie voor details over de juiste aansluitingen voor elke gate. In Jade zijn de gates in de standaard celbibliotheek te vinden in de parts bin onder “/gates/”.
Omdat we op poortniveau ontwerpen, kunnen we een fastersimulator gebruiken die alleen gates en logische waarden kent (in plaats van transistors en spanningen). Merk op dat uw ontwerp geen mosfets, weerstanden, condensatoren, enz. kan bevatten; de simulator op poortniveau ondersteunt alleen de poort-primitieven in de standaard celbibliotheek.Ingangen worden nog steeds gespecificeerd in termen van spanningen (om compatibiliteit met de andere simulators te behouden), maar de gate-level-simulator converteert spanningen naar een van de drie mogelijke logische waarden, gebruikmakend van de vil en vih drempelwaarden die aan het begin van uw ontwerpbestand zijn gespecificeerd:
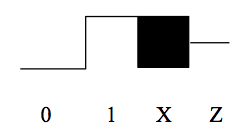
1 logisch hoog (spanningen groter dan of gelijk aan vih drempel)
X onbekend of ongedefinieerd (spanningen tussen de drempelwaarden, of onbekende spanningen)
Een vierde waarde “Z” wordt gebruikt om de waarde weer te geven van knooppunten die niet worden aangestuurd door een gate uitgang (b.v.g., de uitgangen van tristatedrivers die niet zijn ingeschakeld). Het volgende diagram toont hoe deze waarden op het golfvorm-display verschijnen:
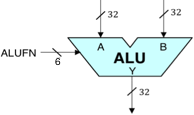 De 32-bit ALU die we zullen bouwen zal een component zijn in de Betaprocessor die we in volgende laboratoria zullen behandelen. Het logicasymbool voor onze ALU staat rechts afgebeeld. Het is een combinatorische schakeling die twee 32-bits datawoorden A en B als inputs neemt, en een 32-bits output Y produceert door een gespecificeerde rekenkundige of logische functie uit te voeren op de A en B inputs. De uit te voeren functie wordt gespecificeerd door een 6-bit controle-ingang, FN, waarvan de waarde de functie codeert volgens de onderstaande tabel:
De 32-bit ALU die we zullen bouwen zal een component zijn in de Betaprocessor die we in volgende laboratoria zullen behandelen. Het logicasymbool voor onze ALU staat rechts afgebeeld. Het is een combinatorische schakeling die twee 32-bits datawoorden A en B als inputs neemt, en een 32-bits output Y produceert door een gespecificeerde rekenkundige of logische functie uit te voeren op de A en B inputs. De uit te voeren functie wordt gespecificeerd door een 6-bit controle-ingang, FN, waarvan de waarde de functie codeert volgens de onderstaande tabel:
| FN | Werking | Uitgangswaarde Y |
|---|---|---|
| CMPEQ | Y = (A == B) | |
| 00-101 | CMPLT | Y = (A < B) |
| 00-111 | CMPLE | Y = (A ≤ B) |
| 01—0 | 32-bit ADD | Y = A + B |
| 01—1 | 32-bit SUBTRACT | Y = A – B |
| 10abcd | Bit-wise Boolean | Y = Fabcd(A,B) |
| 11–00 | Logische verschuiving naar links (SHL) | Y = A << B |
| 11–01 | Logical Shift right (SHR) | Y = A >> B |
| 11–11 | Arithmetic Shift right (SRA) | Y = A >> B (sign extended) |
Merk op dat door het specificeren van een geschikte waarde voor de 6-bit FNinput, de ALU een verscheidenheid aan rekenkundige bewerkingen, vergelijkingen, verschuivingen, en bitwise Booleaanse combinaties kan uitvoeren die onze Beta processor nodig heeft.
| Bi | Ai | Yi |
| 0 | 0 | d |
| 0 | 1 | c |
| 1 | 0 | b |
| 1 | 1 | a |
De bitwise Booleaanse operaties worden gespecificeerd door FN=10; in dit geval worden de resterende FN-bits abcd genomen als punten in de waarheidstabel die beschrijft hoe elk bit van Y wordt bepaald door de overeenkomstige bits van A en B, zoals hiernaast is weergegeven.De drie vergelijkingsoperaties leveren elk een Booleaanse output op. In deze gevallen is Y allemaal nul, en de lage-orde bit Y is een 0 of 1 die de uitkomst van de vergelijking tussen de 32-bits A en B operanden weergeeft. We kunnen het ALU-ontwerp benaderen door het op te splitsen in subsystemen gewijd aan rekenkundige, vergelijkende, Booleaanse en verschuivingsbewerkingen, zoals hieronder weergegeven:
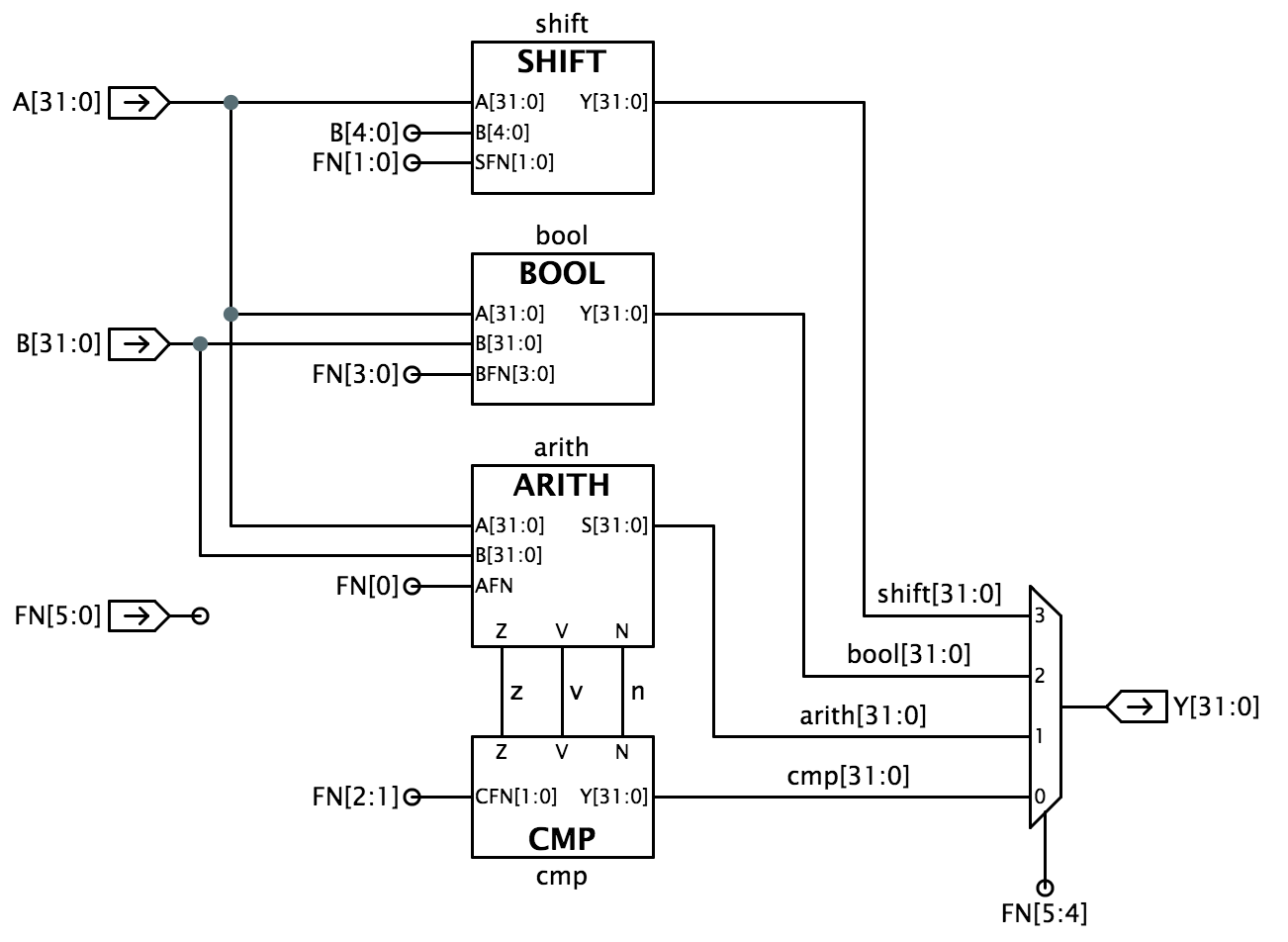
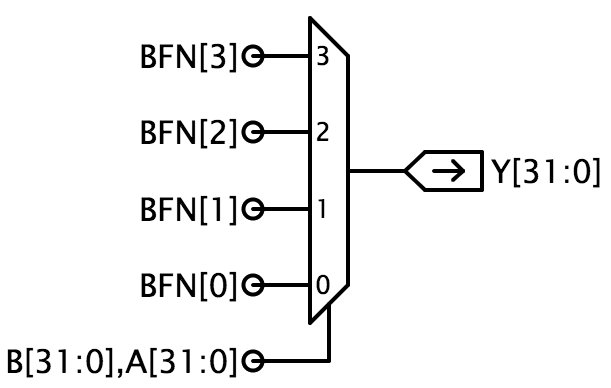 De voorgestelde implementatie gebruikt 32 kopieën van een 4-naar-1-multiplexor (mux4) waarbij BFN de uit te voeren bewerking codeert en A en B aan de selectingangen van de multiplexor worden gehaakt. Deze implementatie kan elk van de 16 2-input Booleaanse functies produceren.
De voorgestelde implementatie gebruikt 32 kopieën van een 4-naar-1-multiplexor (mux4) waarbij BFN de uit te voeren bewerking codeert en A en B aan de selectingangen van de multiplexor worden gehaakt. Deze implementatie kan elk van de 16 2-input Booleaanse functies produceren.
De volgende tabel toont de coderingen voor enkele van de BFN-control signalen die gebruikt worden door de test jig (en in onze typische Betaimplementaties):
| Operation | BFN |
|---|---|
| 1000 | |
| OR | 1110 |
| 0110 | |
| “A” | 1010 |
ARITH-eenheidOntwerp een addder/subtractor (ARITH) eenheid die werkt op 32-bits tweevoudige complementingangen en een 32-bits uitgang genereert. Het zal nuttig zijn om drie andere uitgangssignalen te genereren die door de CMP-eenheid kunnen worden gebruikt: Z, dat waar is als de S-uitgangen allemaal nul zijn, V, dat waar is als de opteloperatie overloopt (d.w.z. als het resultaat te groot is om in 32 bits te worden weergegeven), en N, dat waar is als de som negatief is (d.w.z., S = 1).Overflow kan nooit optreden als de twee operanden van de optelling verschillende tekens hebben; als de twee operanden hetzelfde teken hebben, dan kan overflow worden gedetecteerd als het teken van het resultaat verschilt van het teken van de operanden:

| Vergelijkingsformule voor LSB | CFN | |
|---|---|---|
| A = B | LSB = Z(Z) | 01 |
| A < B | LSB = \(N \oplus V) | 10 |
| A ≤ B | LSB = \(Z + (N \oplus V) | 11 |
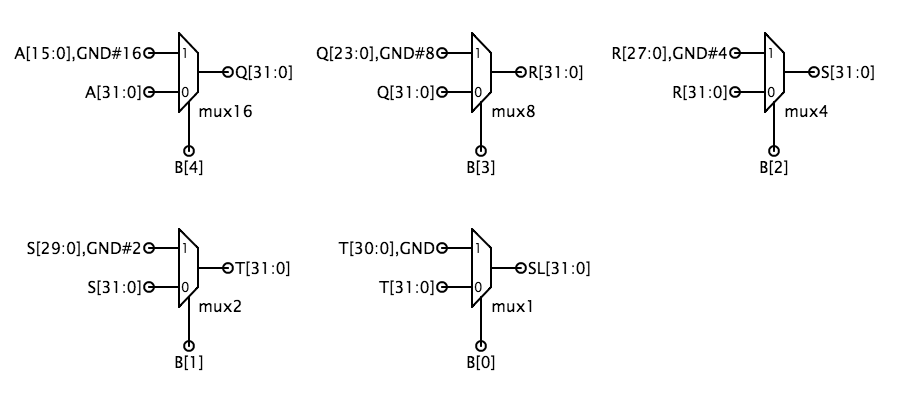
Op het niveau van de ALU-module, FN gebruikt om de vergelijkingseenheid aan te sturen, omdat we FN moeten gebruiken om de optel/aftrek eenheid aan te sturen om een aftrekking te forceren.Opmerking over de prestaties: de ingangen Z, V en N in deze schakeling kunnen pas worden berekend door de optel-/trekkeenheid nadat de 32-bit optelling is voltooid. Dit betekent dat ze vrij laat aankomen en dan verdere bewerking in deze module vereisen, waardoor Y pas zeer laat in het spel verschijnt. Je kunt de zaak aanzienlijk versnellen door na te denken over de relatieve timing van Z, V en N en dan je logica zo te ontwerpen dat vertragingspaden met laat binnenkomende signalen worden geminimaliseerd.De module test zorgt ervoor dat het juiste antwoord wordt gegenereerd voor alle mogelijke combinaties van Z, V, N en CFN. SHIFT-eenheidOntwerp een 32-bit shifter die logische linker shift (SHL), logische rechter shift (SHR) en rekenkundige rechter shift (SRA) uitvoert. De A operand levert de te verschuiven gegevens en de lage-orde 5 bits van de B operand worden gebruikt als de verschuivingstelling (d.w.z. van 0 tot 31 bits van de verschuiving). De gewenste operatie wordt als volgt op SFN gecodeerd:
| Operation | SFN |
|---|---|
| 00 | |
| SHR (shift rechts) | 01 |
| SRA (shift rechts met tekenextensie ) | 11 |
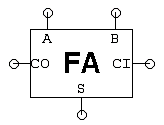
- Een enkele testvector voor de volledige adder bestaat uit 3 ingangswaarden (een voor A, B en CI) en 2 uitgangswaarden (S en CO). Om een test uit te voeren worden de ingangswaarden van de huidige testvector toegepast op het te testen apparaat en vervolgens worden de werkelijke uitgangswaarden vergeleken met de door de testvector genoemde verwachte waarden. Dit proces wordt herhaald totdat alle testvectoren zijn gebruikt. Ervan uitgaande dat we niets weten over de interne schakeling van de volledige adder, hoeveel testvectoren zouden we nodig hebben om de functionaliteit ervan uitputtend te testen? Aantal testvectoren om een volledige opteller uitputtend te testen?
- Zie eens een 32-bit opteller met 64 ingangen (twee 32-bit input operands, waarbij CIN aan massa is gebonden zoals in onderstaand schema) en 32 uitgangen (het 32-bit resultaat). Veronderstel dat we niets weten over de interne schakeling en dus niet kunnen uitsluiten dat die voor een bepaalde combinatie van ingangen een verkeerd antwoord kan geven. Met andere woorden, het feit dat de opteller het juiste antwoord kreeg voor 2 + 3 laat ons niet toe conclusies te trekken over welk antwoord hij zou krijgen voor 2 + 7. Als we elke 100ns een testvector zouden kunnen toepassen, hoe lang zou het dan duren om de adder volledig te testen? Tijd om 32-bit adder uitputtend te testen? (in jaren)
- Het is duidelijk dat het testen van een 32-bit adder door alle combinaties van invoerwaarden uit te proberen geen goed plan is! Hieronder zie je een schema voor een 32-bit ripple-carry-adder.
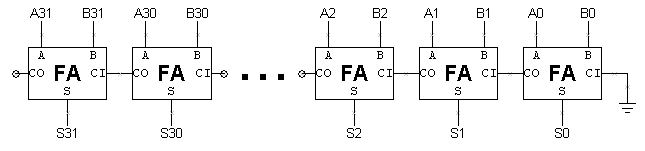 Behalve de carry-in van het bit rechts, werkt elk bit van de opteller onafhankelijk. We kunnen deze observatie gebruiken om de adder bit-voor-bit te testen en met een beetje nadenken kunnen we in feite veel van deze tests parallel uitvoeren. In dit geval zegt het feit dat de opteller het juiste antwoord gaf voor 2 + 3 ons eigenlijk veel over het antwoord dat hij zal krijgen voor 2 + 7. Aangezien de berekening van de bits 0 en 1 van de adder in beide gevallen hetzelfde is, zullen, als het antwoord voor 2 + 3 juist is, de twee bits van de lage orde van het antwoord voor 2 + 7 ook juist zijn. Dus ons plan voor het testen van de ripple-carry adder is om elke volledige adder onafhankelijk te testen. Bij het testen van bit N kunnen we A en B direct vanuit de testvector instellen. Het kost wat meer werk om CI op een bepaalde waarde in te stellen, maar we kunnen het doen met de juiste keuzes voor A en B. Als we CI op 0 willen instellen, op welke waarden moeten A en B dan worden ingesteld? Als we CI op 1 willen zetten? Neem aan dat we niets mogen aannemen over de waarde van CI. Waarden van A en B om C=0 te maken? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Waarden van A en B om C=1 te maken? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Met deze strategie kunnen we de even bits van de adder parallel testen met een set testvectoren en de oneven bits van de adder parallel testen met een andere set testvectoren. Hier is een set van 10 testvectoren die alle combinaties van invoerwaarden voor elke FA in een 32-bit ripple-carry adder zou moeten testen:
Behalve de carry-in van het bit rechts, werkt elk bit van de opteller onafhankelijk. We kunnen deze observatie gebruiken om de adder bit-voor-bit te testen en met een beetje nadenken kunnen we in feite veel van deze tests parallel uitvoeren. In dit geval zegt het feit dat de opteller het juiste antwoord gaf voor 2 + 3 ons eigenlijk veel over het antwoord dat hij zal krijgen voor 2 + 7. Aangezien de berekening van de bits 0 en 1 van de adder in beide gevallen hetzelfde is, zullen, als het antwoord voor 2 + 3 juist is, de twee bits van de lage orde van het antwoord voor 2 + 7 ook juist zijn. Dus ons plan voor het testen van de ripple-carry adder is om elke volledige adder onafhankelijk te testen. Bij het testen van bit N kunnen we A en B direct vanuit de testvector instellen. Het kost wat meer werk om CI op een bepaalde waarde in te stellen, maar we kunnen het doen met de juiste keuzes voor A en B. Als we CI op 0 willen instellen, op welke waarden moeten A en B dan worden ingesteld? Als we CI op 1 willen zetten? Neem aan dat we niets mogen aannemen over de waarde van CI. Waarden van A en B om C=0 te maken? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Waarden van A en B om C=1 te maken? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Met deze strategie kunnen we de even bits van de adder parallel testen met een set testvectoren en de oneven bits van de adder parallel testen met een andere set testvectoren. Hier is een set van 10 testvectoren die alle combinaties van invoerwaarden voor elke FA in een 32-bit ripple-carry adder zou moeten testen:
bits 0, 2, … bits 1, 3, … A B A=0, B=0, CI=0 A=0, B=0, CI=0 0x00000000 0x00000000 A=1, B=0, CI=0 A=0, B=0, CI=0 0x55555555 0x000000 A=0, B=1, CI=0 A=0, B=0, CI=0 0x00000000 0x555555 A=1, B=1, CI=0 A=0, B=0, CI=1 0x555555 0x55555555 A=0, B=0, CI=0 A=1, B=0, CI=0 0xAAAAAA 0x000000 A=0, B=0, CI=0 A=0, B=1, CI=0 0x00000000 0xAAAA A=0, B=0, CI=1 A=1, B=1, CI=0 0xAAAA 0xAAAA 0xAAAA A=1, B=0, CI=1 A=1, B=0, CI=1 0xFFFFFF 0x00000001 A=0, B=1, CI=1 A=0, B=1, CI=1 0x0000000101 0xFFFFFF A=1, B=1, CI=1 A=1, B=1, CI=1 0xFFFFFF 0xFFFFFF - Drie van de ingangen van de vergelijker (Z, V en N) zijn afkomstig van de adder/subtractor die in subtractmodus werkt en A-B berekent:
| Bi | Ai | Yi |
| 0 | 0 | d |
| 1 | c | |
| 1 | 0 | b |
| 1 | 1 | a |
Zoals we zagen in de instructies voor de ALU,worden de bitwise Booleaanse operaties gespecificeerd door FN=10. In dit geval worden de resterende FN-bits abcd genomen als punten in de waarheidstabel die beschrijft hoe elk bit van Y wordt bepaald door de overeenkomstige bits van A en B, zoals hiernaast is weergegeven. Bepaal voor elk van de onderstaande Booleaanse bewerkingen de instellingen voor FN zodat de Bool-eenheid de gewenste bewerking zal berekenen. AND(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 OR(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 XOR(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 NAND(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 NOR(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 XNOR(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 A: FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 B: FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111