Backpropagation Stap voor Stap

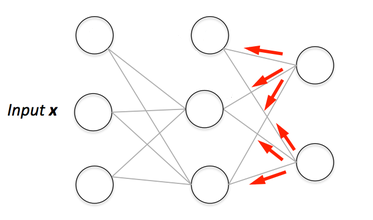Als je je eigen neurale netwerk bouwt, moet je zeker begrijpen hoe je het moet trainen.Backpropagation is een veelgebruikte techniek om neurale netwerken te trainen. Er zijn veel bronnen die de techniek uitleggen, maar deze post zal backpropagation uitleggen met concreet voorbeeld in een zeer gedetailleerde kleurrijke stappen.

U kunt visualisatie van de forward pass en backpropagation hier zien. U kunt uw neurale netwerk bouwen met netflow.js

Overzicht

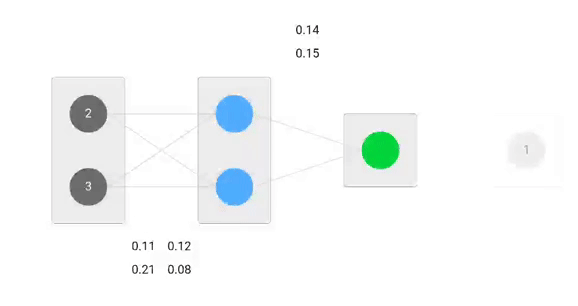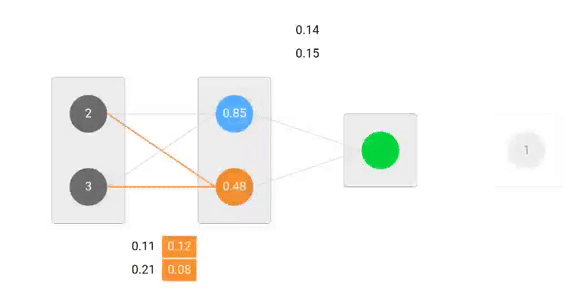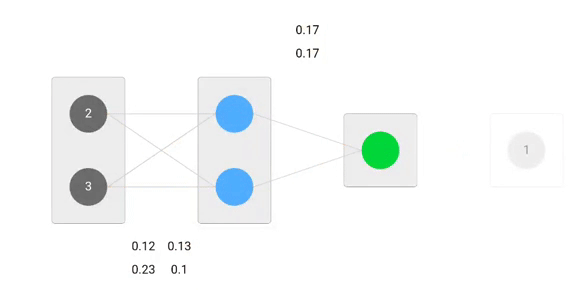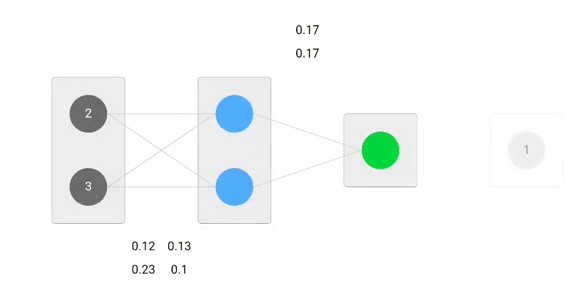
In deze post zullen we een neuraal netwerk met drie lagen bouwen:

• Invoerlaag met twee ingangsneuronen
• Een verborgen laag met twee neuronen
• Uitgangslaag met één neuron

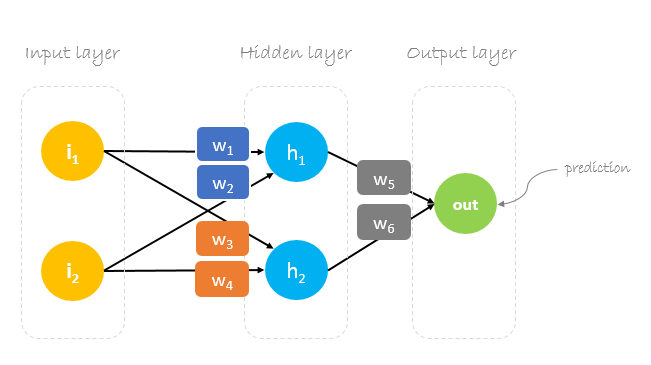
Wichten, gewichten, gewichten

Een neuraal netwerk trainen gaat over het vinden van gewichten die de voorspellingsfout minimaliseren. We beginnen de training gewoonlijk met een set willekeurig gegenereerde gewichten. Vervolgens worden de gewichten met behulp van backpropagation bijgewerkt in een poging willekeurige invoer correct in uitvoer om te zetten.

Onze aanvankelijke gewichten zijn als volgt:w1 = 0.11w2 = 0.21w3 = 0.12w4 = 0.08w5 = 0.14 en w6 = 0.15

Dataset

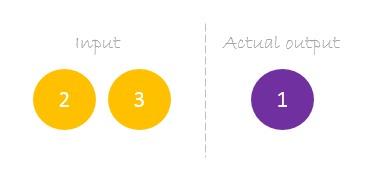
Onze dataset heeft één monster met twee ingangen en één uitgang.

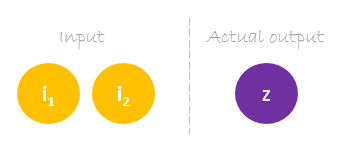
Onze enkele steekproef ziet er als volgt uit inputs= en output=.

Forward Pass

We gebruiken de gegeven gewichten en invoergegevens om de uitvoer te voorspellen. Inputs worden vermenigvuldigd met gewichten; de resultaten worden vervolgens doorgegeven aan de volgende laag.

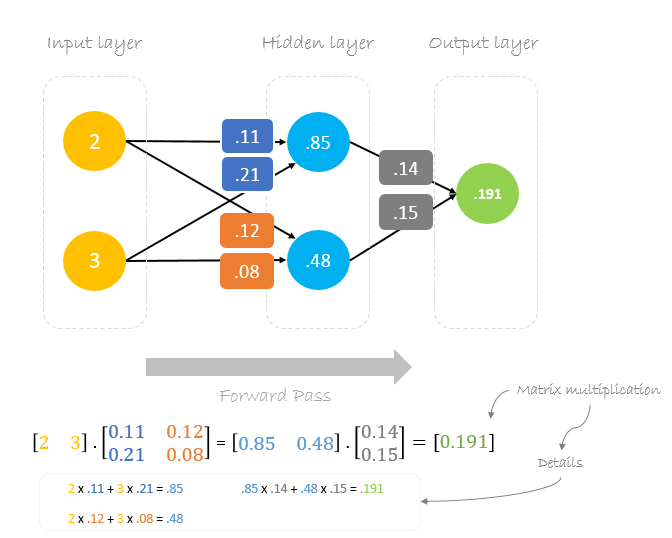
Fout berekenen

Nu is het tijd om te kijken hoe ons netwerk heeft gepresteerd door het verschil te berekenen tussen de werkelijke output en de voorspelde output. Het is duidelijk dat de output van ons netwerk, of de voorspelling, niet eens in de buurt komt van de werkelijke output. We kunnen het verschil of de fout als volgt berekenen.

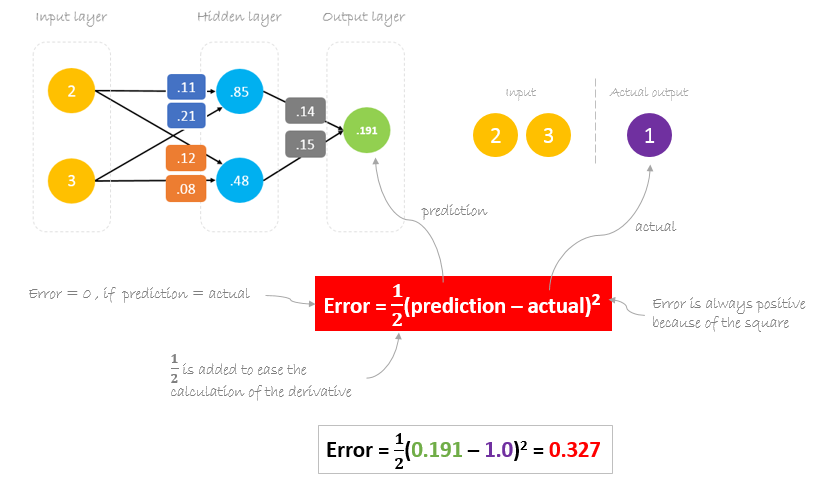
Reducing Error

Het belangrijkste doel van de training is om de fout of het verschil tussen de voorspelling en de werkelijke uitvoer te verkleinen. Aangezien de werkelijke uitvoer constant is, “niet verandert”, is de enige manier om de fout te verminderen het veranderen van de voorspellingswaarde. De vraag is nu, hoe de voorspellingswaarde te veranderen?

Door de voorspelling in zijn basiselementen te ontleden, kunnen we vaststellen dat gewichten de variabele elementen zijn die de voorspellingswaarde beïnvloeden. Met andere woorden, om de voorspellingswaarde te veranderen, moeten we de waarden van de gewichten veranderen.

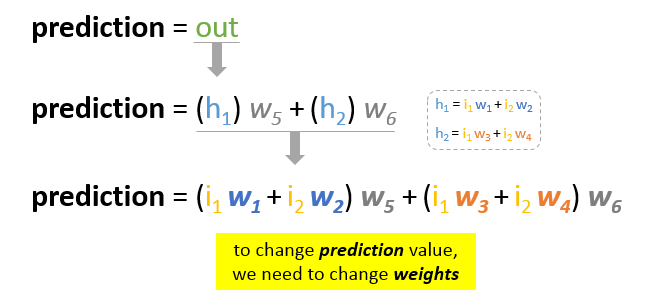
De vraag is nu hoe we de waarde van de gewichten kunnen veranderen zodat de fout afneemt?
Het antwoord is Backpropagation!

Backpropagation

Backpropagation, kort voor “achterwaartse voortplanting van fouten”, is een mechanisme dat wordt gebruikt om de gewichten bij te werken met behulp van gradient descent. Het berekent de gradiënt van de foutfunctie ten opzichte van de gewichten van het neurale netwerk. De berekening gaat achterwaarts door het netwerk.

Gradiënt afdaling is een iteratief optimalisatie algoritme voor het vinden van het minimum van een functie; in ons geval willen we de error functie minimaliseren. Om een lokaal minimum van een functie te vinden met behulp van gradiënt-afdaling, neemt men stappen evenredig met het negatieve van de gradiënt van de functie op het huidige punt.

Voor het bijwerken van w6, nemen we de huidige w6 en trekken we de gedeeltelijke afgeleide van de foutfunctie af ten opzichte van w6. Optioneel vermenigvuldigen we de afgeleide van de foutfunctie met een gekozen getal om er zeker van te zijn dat het nieuwe bijgewerkte gewicht de foutfunctie minimaliseert; dit getal wordt leersnelheid genoemd.

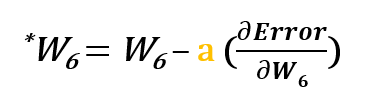
De afgeleide van de foutenfunctie wordt geëvalueerd door de kettingregel als volgt toe te passen

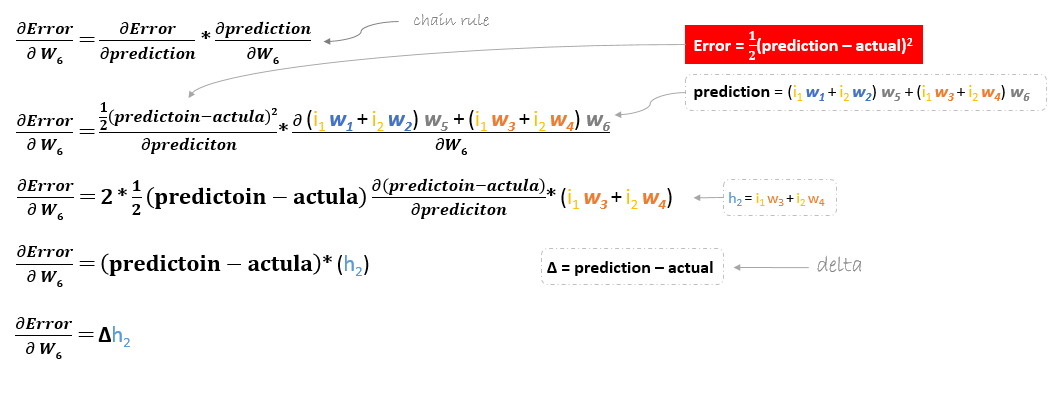
Om w6 bij te werken kunnen we dus de volgende formule toepassen

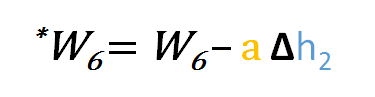
Op dezelfde manier kunnen we de update-formule afleiden voor w5 en alle andere gewichten die tussen de uitvoer en de verborgen laag bestaan.

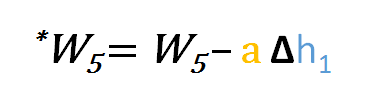
Bij het teruggaan om w1w2w3 en w4 die tussen invoer en verborgen laag bestaan, bij te werken, zal de gedeeltelijke afgeleide voor de foutfunctie met betrekking tot w1, bijvoorbeeld, als volgt zijn.

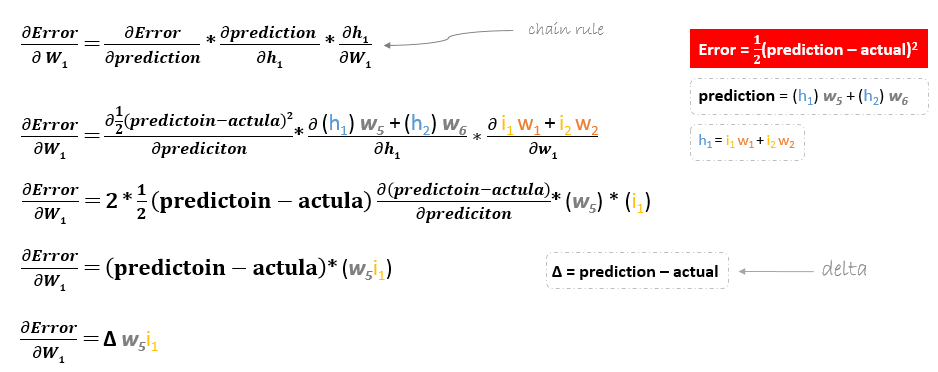
We kunnen de update-formule voor de overige gewichten w2w3 en w4 op dezelfde manier vinden.

Samengevat zullen de update-formules voor alle gewichten er als volgt uitzien:

We kunnen de update-formules in matrices als volgt herschrijven

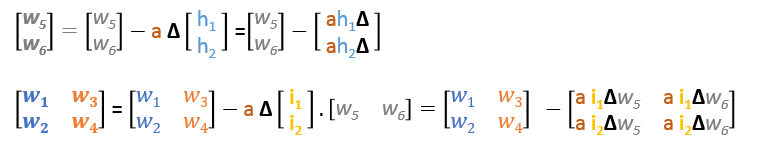
Backward Pass

Met behulp van afgeleide formules kunnen we de nieuwe gewichten vinden.

Learning rate: is een hyperparameter, wat betekent dat we de waarde ervan handmatig moeten raden.

Nu, met behulp van de nieuwe gewichten herhalen we de voorwaartse doorloop

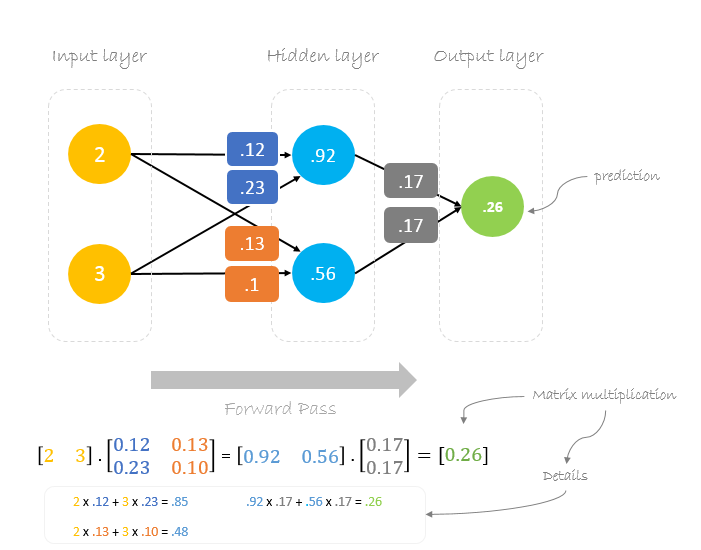
We kunnen zien dat de voorspelling 0.26 een beetje dichter bij de werkelijke uitvoer ligt dan de eerder voorspelde 0.191. We kunnen hetzelfde proces van achterwaartse en voorwaartse pass herhalen totdat de fout dichtbij of gelijk aan nul is.

Backpropagation Visualization

U kunt de visualisatie van de voorwaartse pass en backpropagation hier bekijken.

U kunt uw neurale netwerk bouwen met netflow.js