Chang Hsin Lee
Wanneer ik een machine learning model bouw voor classificatieproblemen, is een van de vragen die ik mezelf stel: waarom is mijn model niet crap? Soms heb ik het gevoel dat het ontwikkelen van een model is als het vasthouden van een granaat, en kalibratie is een van mijn veiligheidsspelden. In deze post zal ik het concept van kalibratie doorlopen, en vervolgens in Python laten zien hoe je diagnostische kalibratieplots kunt maken.
Hier is de link naar het Jupyter-notebook voor deze post
Evalueren van probabilistische voorspellingen
Laat me beginnen met uit te leggen wat kalibratie is en waar het idee vandaan komt.
In machine learning produceren de meeste classificatiemodellen voorspellingen van klassenwaarschijnlijkheden tussen 0 en 1, en hebben dan een optie om probabilistische outputs om te zetten in klassevoorspellingen. Zelfs algoritmen die alleen scores produceren, zoals support vector machine, kunnen worden omgebouwd om waarschijnlijkheids-achtige voorspellingen te produceren.
Voor een binair classificatieprobleem zijn er samenvattende metrieken – nauwkeurigheid, precisie, recall, F1-score, enzovoort – die de kwaliteit van binaire 0’s en 1’s outputs evalueren. Als de outputs niet binair zijn maar zwevende getallen tussen 0 en 1, dan kan ik ze gebruiken als scores voor de rangschikking. Maar zwevende getallen tussen 0 en 1 schreeuwen waarschijnlijkheden, en hoe weet ik of ik ze als waarschijnlijkheden kan vertrouwen?
De output van een model kan worden gezien als een verklaring die zegt hoe waarschijnlijk het is dat iets zal gebeuren. Een voorbeeld van zo’n model – waarvan ik de uitspraken elke dag controleer voordat ik mijn huis verlaat – is de weerdienst. In het bijzonder, hoe waarschijnlijk is het dat het gaat regenen?
 afbeelding van weather.com
afbeelding van weather.com
Het weerbericht zegt dat er zondag 80% kans is op regen. Hoe betrouwbaar is die 80%? Als ik de voorspellingen van weather.com uit het verleden bekijk en ontdek dat 8 van de 10 dagen regenachtig zijn als ze 80% voorspellen, dan kan ik mezelf ervan overtuigen mijn luisterboeken in te laden en me voor te bereiden op het drukke verkeer op de snelweg in de middag.
Met andere woorden, een nauwkeurige weersvoorspelling betekent dat als ik 100 dagen bekijk waarop 80% kans op regen wordt voorspeld, dat er dan ongeveer 80 regenachtige dagen moeten zijn. Het moet ook accuraat zijn in andere waarschijnlijkheidsbereiken. Voor dagen die worden voorspeld met 30% kans op regen, zouden er gemiddeld 30 regenachtige dagen op de 100 dagen moeten zijn. Als de voorspellingen van deze weersvoorspellingsdienst allemaal dit goede patroon volgen, dan zeggen we dat hun voorspellingen gekalibreerd zijn. Dat is de probabilistische manier om te zeggen dat ze de spijker op zijn kop slaan.
- Een probabilistisch model is gekalibreerd als ik de testmonsters op basis van hun voorspelde kansen in kubussen verdeel, waarbij de werkelijke uitkomsten van elke kubus een verhouding hebben die dicht bij de kansen in de kubus ligt.
Hoe beoordeel ik kalibratie? In plaats van de kalibratie in één getal samen te vatten, maak ik liever kalibratieplots.
Kalibratieplots zijn vaak lijnplots. Als ik eenmaal het aantal bins heb gekozen en voorspellingen in de bin heb gegooid, wordt elke bin omgezet in een punt op de plot. Voor elke bin is de y-waarde het aandeel ware uitkomsten, en de x-waarde de gemiddelde voorspelde kans. Een goed gekalibreerd model heeft dus een kalibratiekromme die de rechte lijn y=x benadert. Hier is een voorbeeld van een kalibratieplot met twee curven, die elk een model op dezelfde gegevens vertegenwoordigen.
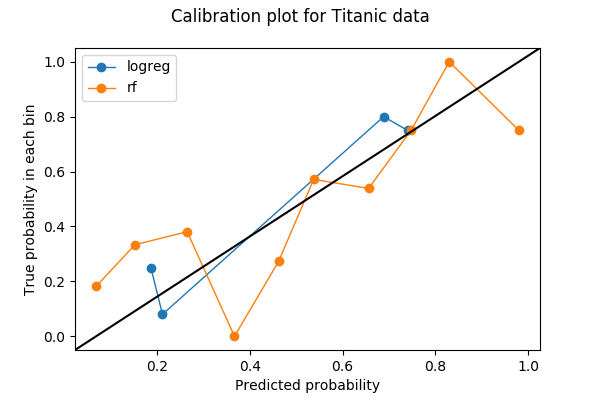
Ik ga laten zien hoe ik deze plot in Python heb gemaakt en wat ik erin heb gezien.
Een Python-voorbeeld
Het eerste wat je moet doen bij het maken van een kalibratieplot is het kiezen van het aantal bins. In dit voorbeeld heb ik de waarschijnlijkheden verdeeld in 10 bins tussen 0 en 1: van 0 tot 0,1, 0,1 tot 0,2, …, 0,9 tot 1. De data die ik heb gebruikt is de Titanic dataset van Kaggle, waar het te voorspellen label een binaire variabele is Survived.
Ik ga de kalibratiecurves voor twee modellen plotten – een voor logistische regressie, en een voor random forest. Beide modellen produceren klassenwaarschijnlijkheden voor Survived op basis van twee kenmerken Age en Sex.
+----+------+--------+| Age| Sex|Survived|+----+------+--------+|22.0| male| 0||38.0|female| 1||26.0|female| 1|+----+------+--------+Voorbewerking
Voor het trainen van mijn modellen heb ik de ontbrekende waarden in Age opgevuld met het gemiddelde ervan en heb ik Sex ook veranderd in een numerieke variabele met waarden 0 en 1.
import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn import preprocessingfrom sklearn import model_selectiontitanic = pd.read_csv('train.csv')fitted_age_imputer = preprocessing.Imputer(axis=1).fit(titanic.values)titanic = fitted_age_imputer.transform( titanic.values.reshape(1, -1) ).transpose()titanic = np.where(titanic.Sex == 'female', 1, 0)Daarna heb ik de gegevens opgesplitst in een training- en een validatieset met een 80/20-verdeling.
from sklearn import model_selectionfeature_cols = feature_train, feature_test, label_train, label_test = ( model_selection.train_test_split( titanic, titanic.Survived, test_size=0.2, random_state=1) )Trainen en voorspellen
Ik kan nu een logistisch regressiemodel trainen op mijn trainingsset en voorspellen op de validatieset.
from sklearn.linear_model import LogisticRegressionlogreg_model = LogisticRegression().fit(X=feature_train,y=label_train)logreg_prediction = logreg_model.predict_proba(feature_test)Op vergelijkbare wijze kun je een random forest-model trainen en voorspellen op de validatieset.
from sklearn.ensemble import RandomForestClassifierrf_model = RandomForestClassifier(random_state=1234).fit(X=feature_train, y=label_train)rf_prediction = rf_model.predict_proba(feature_test)De positieve klassenwaarschijnlijkheid wordt geretourneerd door de modellen in de tweede kolom (index=1):
logreg_predictionarray(, , , , ])Kalibratieplot
Als ik eenmaal de klassenwaarschijnlijkheden en labels heb, kan ik de bins voor een kalibratieplot berekenen. Hier gebruik ik sklearn.calibration.calibration_curve dat de (x,y) coördinaten van de bins op de kalibratieplot teruggeeft.
from sklearn.calibration import calibration_curvelogreg_y, logreg_x = calibration_curve(label_test, logreg_prediction, n_bins=10)Merk op dat hoewel ik voor logistische regressie om 10 bins heb gevraagd, 6 bins van de 10 geen gegevens hebben. De reden hiervoor is een combinatie van het feit dat logistische regressie een eenvoudig model is, dat er slechts twee kenmerken zijn en dat ik minder dan 200 datapunten in de validatieset heb.
), array()]Volgende bereken ik de coördinaten voor de bins van het random forest-model.
rf_y, rf_x = calibration_curve(label_test, rf_prediction, n_bins=10)Nu kan ik de twee kalibratiecurven plotten. Om de plot leesbaarder te maken, heb ik ook een y=x-referentielijn toegevoegd op basis van een StackOverflow-antwoord.
%matplotlib inlineimport matplotlib.pyplot as pltimport matplotlib.lines as mlinesimport matplotlib.transforms as mtransformsfig, ax = plt.subplots()# only these two lines are calibration curvesplt.plot(logreg_x,logreg_y, marker='o', linewidth=1, label='logreg')plt.plot(rf_x, rf_y, marker='o', linewidth=1, label='rf')# reference line, legends, and axis labelsline = mlines.Line2D(, , color='black')transform = ax.transAxesline.set_transform(transform)ax.add_line(line)fig.suptitle('Calibration plot for Titanic data')ax.set_xlabel('Predicted probability')ax.set_ylabel('True probability in each bin')plt.legend()plt.show()
Bin-totalen en discriminatie
Er zijn slechts 4 niet-lege bins voor logistische regressie terwijl ik om 10 bins had gevraagd. Is dit een slechte zaak? Laten we een functie gebruiken die ik uit de broncode van sklearn.calibration.calibration_curve heb gehaald om uit te zoeken welke de ontbrekende bins zijn.
def bin_total(y_true, y_prob, n_bins): bins = np.linspace(0., 1. + 1e-8, n_bins + 1) # In sklearn.calibration.calibration_curve, # the last value in the array is always 0. binids = np.digitize(y_prob, bins) - 1 return np.bincount(binids, minlength=len(bins))bin_total(label_test, logreg_prediction, n_bins=10)array(, dtype=int64)De ontbrekende bins hebben middenwaarden van 5%, 35%, 45%, 55%, 85% en 95%. In feite kan het hebben van lage totalen of lege bakken in de middelste bakken (30-60%) een goede zaak zijn – ik wil dat mijn voorspellingen deze middelste bakken vermijden en discriminerend worden.
Discriminatie is een concept dat bij classificatieproblemen zij aan zij gaat met kalibratie. Soms komt het vóór de kalibratie als het doel bij het bouwen van een model is om automatische beslissingen te nemen in plaats van statistische schattingen te geven. Stel je het scenario voor waarin ik twee weermodellen heb en in Podunk, Nevada woon waar 10% (36 dagen per jaar) van de dagen regenachtig zijn:
- model A zegt altijd dat er 10% kans op regen is, ongeacht welke dag het is.
- model B zegt dat het in juni elke dag gaat regenen (100%), en in de andere 11 maanden nooit (0%).
Model A is perfect gekalibreerd. Er is maar één bak – de bak van 10% – en de echte kans is 10%. Model B wijkt echter iets af van de ijking, omdat er 30 dagen in de 100%-bak zullen zijn, maar ook 6 regendagen in de 0%-bak. Maar model B is duidelijk bruikbaarder als ik plannen maak voor een weekendwandeling. Model B is discriminerender dan A, omdat het makkelijker is om beslissingen te nemen (wel of niet wandelen) op basis van de uitkomsten van model B.
Discriminatie wordt vaak gecontroleerd met de receiver operating characteristic curves, of ROC curves, maar dat is een onderwerp voor een andere post.
Cross-validation?
Als discriminatie me niet interesseert en ik alleen een goede kalibratie wil, dan lijkt logistische regressie (blauw) het beter te doen dan random forest (oranje). Is dat echt zo? Als ik met name kijk naar het aantal punten in de bins voor random forest,
bin_total(label_test, rf_prediction, n_bins=10)array(, dtype=int64)Ik vermoed dat het probleem kan zijn dat sommige bins te weinig datapunten hebben. Ik heb 200 punten in 10 bins gestopt, dus sommige bins krijgen er maar een paar, waardoor de kalibratieplot lijdt omdat één verkeerde classificatie in een kleine bin de proportie sterk verandert.
Slechts 20% van mijn gegevens werd in de vorige plot gebruikt, dus misschien kan ik meer gebruiken. Om al mijn gegevens te gebruiken voor het testen van kalibratie tussen verschillende modellen, dacht ik dat ik het idee van kruisvalidatie kan stelen. Als ik mijn data opdeel in 5 vouwen voor kruisvalidatie, dan zal elke vouw eenmaal gebruikt worden als validatieset. Daarom kan ik de voorspelde kansen van alle 5 vouwen samenvoegen en er een kalibratie-plot van maken. Het resultaat van een 5-voudige kalibratieplot is de volgende plot. De code is te vinden in de laatste sectie van het Jupyter-notebook.
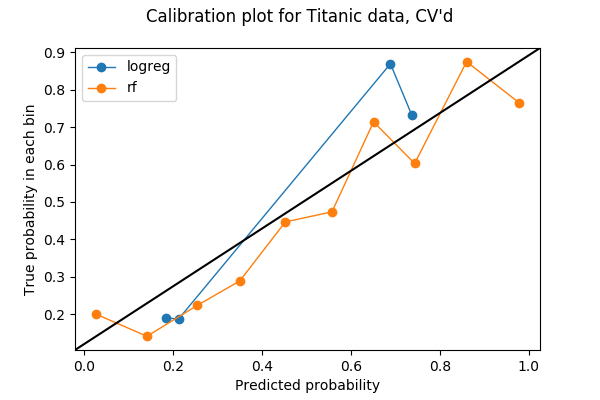
Elke bin heeft nu meer punten:
array(, dtype=int64)en ik denk dat het veilig is om te zeggen dat, in dit voorbeeld, de random forest beter is gekalibreerd dan de logistische regressie.
***
Nate Silver heeft een geweldig voorbeeld over weerkalibratie in het boek The Signal and the Noise, waarin hij de voorspellingen van drie bronnen – de National Weather Service, het Weerkanaal en lokale nieuwszenders – bestudeerde in hoofdstuk 4, You’ve Been Telling Us That Rain Is Green. Hij concludeerde dat de meeste lokale nieuwszenders slecht gekalibreerd zijn en “nat” zijn. Het is een juweeltje, en ik raad aan het boek op te halen als je het in handen kunt krijgen.
Ik leerde voor het eerst over kalibratie via mijn collega Kevin in 2016 toen we verschillende metrieken over classificatiemodellen bespraken. Zonder hem zal het waarschijnlijk nog een jaar of twee duren voordat ik het belang van kalibratie inzie, en veel later voordat ik deze post schrijf.