College Algebra

Om de omvang van aardbevingen te analyseren of de omvang van twee verschillende aardbevingen te vergelijken, moeten we kunnen omrekenen tussen de logaritmische en exponentiële vorm. Stel bijvoorbeeld dat de hoeveelheid energie die bij de ene aardbeving vrijkwam 500 keer zo groot was als de hoeveelheid energie die bij een andere aardbeving vrijkwam. We willen het verschil in magnitude berekenen. De vergelijking die dit probleem voorstelt is {10}^{x}=500 waarbij x het verschil in magnitudes op de schaal van Richter voorstelt. Hoe lossen we x op?

We hebben nog geen methode geleerd om exponentiële vergelijkingen algebraïsch op te lossen. Geen van de tot nu toe besproken algebraïsche hulpmiddelen is voldoende om {10}^{x}=500 op te lossen. We weten dat {10}^{2}=100 en {10}^{3}=1000, dus het is duidelijk dat x een waarde tussen 2 en 3 moet zijn omdat y={10}^{x} stijgend is. We kunnen een grafiek bekijken om de oplossing beter te kunnen schatten.

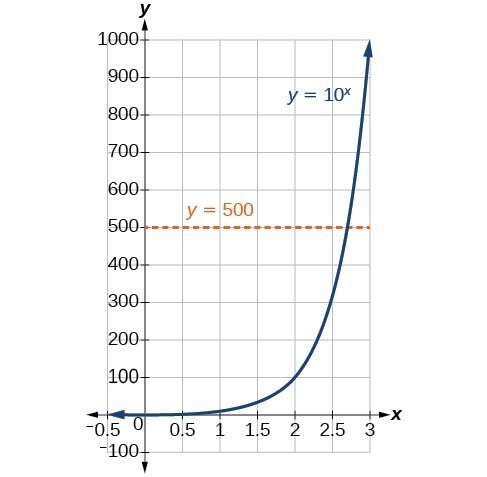
Een schatting maken uit een grafiek is echter onnauwkeurig. Om een algebraïsche oplossing te vinden, moeten we een nieuwe functie introduceren. Merk op dat de bovenstaande grafiek de horizontale lijntest doorstaat. De exponentiële functie y={b}^{x} is één-op-één, dus haar inverse, x={b}^{y} is ook een functie. Zoals met alle inverse functies het geval is, verwisselen we x en y en lossen we y op om de inverse functie te vinden. Om y als een functie van x voor te stellen, gebruiken we een logaritmische functie van de vorm y={log}_{b}(xrechts). De logaritme met basis b van een getal is de exponent waarmee we b moeten verhogen om dat getal te krijgen.

We lezen een logaritmische uitdrukking als, “De logaritme met basis b van x is gelijk aan y,” of, vereenvoudigd, “log basis b van x is y.” We kunnen ook zeggen, “b verheven tot de macht van y is x,” omdat logs exponenten zijn. Bijvoorbeeld, de logaritme van 32 is 5, omdat 5 de exponent is die we op 2 moeten toepassen om 32 te krijgen. Omdat {2}^{5}=32, kunnen we {{log}_{2}32=5 schrijven. We lezen dit als “log basis 2 van 32 is 5.”

We kunnen het verband tussen de logaritmische vorm en de bijbehorende exponentiële vorm als volgt uitdrukken:

{log}_{b}_left(x}rechts)=y {b}^{y}=x,b>0,b1

Merk op dat de basis b altijd positief is.

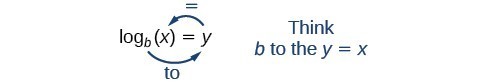
Omdat een logaritme een functie is, wordt deze het best geschreven als {{log}_{b}}left(xrechts), waarbij haakjes worden gebruikt om de evaluatie van de functie aan te geven, net zoals we dat zouden doen met fleft(xrechts). Wanneer de invoer echter één variabele of getal is, is het gebruikelijk om de haakjes weg te laten en de uitdrukking zonder haakjes te schrijven als {{mathrm{log}}_{b}x. Merk op dat veel rekenmachines haakjes rond de x vereisen.

We kunnen de notatie van logaritmen als volgt illustreren:

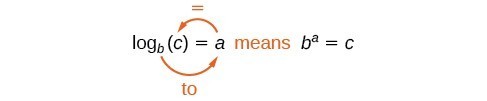
Merk op dat bij het vergelijken van de logaritmische functie en de exponentiële functie, de invoer en de uitvoer worden verwisseld. Dit betekent dat y={log}_{b} links(xrechts) en y={b}^{x} inverse functies zijn.