Column Buckling Equations and Buckling Behaviour | DegreeTutors.com

In de laatste post in deze serie hebben we een aantal kernbegrippen geïntroduceerd aan de hand van een vereenvoudigde geïdealiseerde constructie. In dit artikel gaan we meer realistische constructies bekijken en de kolomknikvergelijkingen bepalen. In het bijzonder zullen we een uitdrukking bepalen voor een kritische belasting voor een axiaal belaste kolom met vastgepinde uiteinden. Daarna onderzoeken we enkele andere steuncondities.

📓 Dit artikel is deel twee van een driedelige serie over het knikken van kolommen. U kunt de complete driedelige serie, mooi opgemaakt en getypt in een ebook, gratis downloaden.

Hierin behandelen we een heleboel, dus hier is een inhoudsopgave…

Kolommen aan beide uiteinden vastgepind
- Opstellen van de differentiaalvergelijking
- Oplossen van de differentiaalvergelijking
- Oplossen van de integratieconstanten
knikmodes en modusvormen
- Maximale doorbuiging onder kritische belasting
- Hogere orde knikmodes
Kolommen met andere ondersteuningscondities
- Vast-Vast
- Vast-Vrij
- Vast-Gepend
Kritische spanning
Effectieve lengte van de kolom

Wanneer we het hebben over een steunpunt met pennen, is dit een steun die geen weerstand biedt tegen verdraaiing. Soms komen we in de praktijk pin supports tegen die deze theoretische definitie zeer dicht benaderen. Hier zijn enkele voorbeelden:

In het kader van onze discussie hier, gaan we ervan uit dat we te maken hebben met pinsteunen zoals deze, en dat ze de rotatie van de constructie niet belemmeren.

1.0 Knikvergelijking voor aan beide uiteinden vastgepinde kolommen

Om deze constructie te analyseren gaan we gebruik maken van de differentiaalvergelijking van de doorbuigingskromme waarin het inwendige buigmoment bij een gegeven doorsnede is, de zijdelingse doorbuiging van de kolom voorstelt en de afstand over de lengte van de kolom. wordt de buigstijfheid genoemd en is het product van Young’s modulus en het tweede moment van de oppervlakte van de doorsnede .

$\begin{align*}EI\frac{\mathrm{d}^2v}{\mathrm{dx^2}}=M\end{align*}$

💡Deze vergelijking modelleert eenvoudig de doorbuigende vorm van de kolom voor een gegeven buigstijfheid.

U bent deze vergelijking waarschijnlijk al elders in uw ingenieursstudie tegengekomen. Onze zijdelings doorgebogen kolom gedraagt zich op vrijwel dezelfde manier als een balk. Vergeet niet dat knikken eerder een buigingsfout is dan een fout door directe compressie (verbrijzeling). Onze taak is nu om deze vergelijking te gebruiken om een uitdrukking af te leiden voor de kritische axiale belasting in een kolom met een pinned-end.

📌 Net als bij de geïdealiseerde structuur die we in de vorige post hebben besproken, gaan we er bij onze afleiding ook hier van uit dat alle doorbuigingen klein zijn in vergelijking met de afmetingen van de structuur.

Opstellen van de differentiaalvergelijking

Eerst beschouwen we de constructie, de afgebogen vorm en het vrij-lichaamsdiagram dat ontstaat als de constructie op een afstand van de onderste steun wordt doorgesneden…

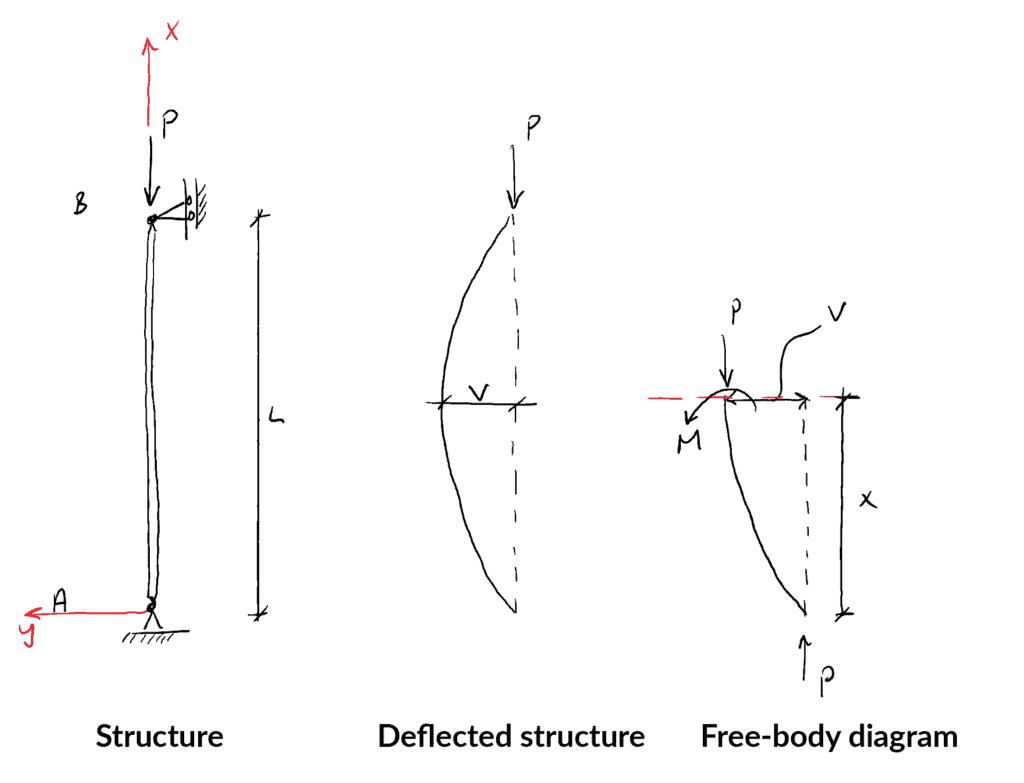
Het nemen van momenten rond punt A levert op:

Herindeling van in de differentiaalvergelijking van de afbuigingscurve en licht herschikken levert op:

$begin{align*}\frac{Mathrm{d}^2v}{\mathrm{d}x^2} + \frac{P}{EI}v=0$

Dit is een lineaire, homogene, 2e orde differentiaalvergelijking met constante coëfficiënten. Toevallig is het ook een vergelijking die de afgebogen vorm van onze constructie modelleert en , de axiale belasting, bevat. Als we dezelfde aanpak volgen als bij de eerder besproken geïdealiseerde constructie, kunnen we, als we deze vergelijking oplossen, $P_{cr}$ bepalen, de waarde van de uitgeoefende belasting waarbij deze in evenwicht wordt gebracht door de buigweerstand van de kolom.

We staan dus voor de taak een differentiaalvergelijking op te lossen. Op dit punt is het handig om te kunnen wijzen op de algemene oplossing van deze vorm van differentiaalvergelijking:

$begin{align*}v(x) = C_1 \sin-links(\sqrt{\frac{P}{EI}}x rechts) + C_2 \cos-links(\sqrt{\frac{P}{EI}}x rechts)\eind{align*}$

Oplossen van de differentiaalvergelijking

Als je op dit punt een omweg wilt maken om te zien hoe de differentiaalvergelijking wordt opgelost, bekijk dan de video hieronder. Anders gaan we in de volgende paragraaf verder met het uitwerken van de integratieconstanten.

Oplossen voor de integratieconstanten

Nu we de algemene oplossing voor dit formaat vergelijking hebben, moeten we de integratieconstanten oplossen met behulp van de randvoorwaarden (pinned-pinned) voor onze kolom.

Grensvoorwaarde 1:

Aan (basis van de kolom aan pinsteun), (de zijwaartse doorbuiging moet gelijk zijn aan nul. Het opleggen van deze voorwaarden aan onze algemene oplossing levert op:

$begin{align*}0=C_1_sin(0) + C_2_cos(0)²eind{align*}$

Daarom

Als resultaat reduceert onze oplossing tot:

$begin{align*}v(x)=C_1(\sin \links(\sqrt{\frac{P}{EI}}x rechts)\eind{align*}$

Grensvoorwaarde 2:

Aan (bovenkant van de kolom aan pinsteun), (zijdelingse doorbuiging ook nul). Opnieuw opleggen van deze randvoorwaarden levert op,

begin{align*}0=C_1sinlinks(\sqrt{\frac{P}{EI}}L rechts)\eind{align*}” class=”alignleft”>

Dus, ofwel is gelijk aan nul of is gelijk aan nul of is gelijk aan nul of iv id=”\sin(…) is gelijk aan nul. Als gelijk is aan nul, dan is aan de vergelijking voldaan voor elke waarde van . Dit brengt ons niet echt verder… we kunnen deze oplossing beschouwen als de triviale oplossing. Van meer belang is het geval waarin:

$\begin{align*}\sin\left(\sqrt{\frac{P}{EI}}L\right)=0\end{align*}$

Wetende wat we weten over $\sin$ functies, kan deze vergelijking alleen waar zijn, wanneer,

$begin{align*}\sqrt{\frac{P}{EI}}L = 0, \pi, 2\pi,...$

We kunnen het geval waarin,

$>begin{align*}\sqrt{\frac{P}{EI}}L = 0$

In dit scenario, gelijk moeten zijn aan nul (omdat alle andere termen per definitie waarden hebben die niet gelijk zijn aan nul) en we weten dat dit niet het geval is. Dus voor een vastgepinde kolom is onze oplossing:

$\begin{align*}\sqrt{\frac{P}{EI}}L = n\pi\end{align*}$

$begin{align*}:sqrt{\frac{P}{EI}}L = n{p>eind{align*}$

waarbij … Tenslotte kunnen we deze vergelijking herschikken om het onderwerp van de vergelijking te maken:

$begin{align*}P={n^2pi^2EI}{L^2}{L^2}$

Voor …

📌 Deze vergelijking stelt een oneindige reeks knikbelastingen voor. De laagste is de kritische knikbelasting, ook wel bekend als de Euler Buckling Load .

$>begin{align*}P_E = \frac{\pi^2EI}{L^2}$

2.0 Knikmodes en modusvormen

Tot nu toe hebben we vastgesteld dat er een oneindige reeks knikbelastingen bestaat en dat de laagste knikbelasting de kritische is en de Euler knikbelasting wordt genoemd. Dit roept de vraag op waar de grotere knikbelastingen mee overeenkomen?

Dit zijn belastingen die overeenkomen met hogere knikmodes. Elke knikvorm heeft een bijbehorende knikvorm. Om dit verder te onderzoeken, verwijzen we terug naar onze algemene oplossing nadat we hebben vastgesteld dat :

$begin{align*}v(x)=C_1 sin \links(\sqrt{\frac{P}{EI}}x rechts)\eind{align*}$

Toepassing van onze tweede randvoorwaarde resulteerde in het vaststellen van de relatie:

$\begin{align*}\sqrt{\frac{P}{EI}}L = n\pi\end{align*}$

Het combineren van deze twee vergelijkingen levert op:

$\begin{align*}v(x)=C_1\sin\left(\frac{n\pi x}{L} \right)\end{align*}$ $begin{align*}v(x)=C_1}sin-links(\frac{n\pi x}{L} rechts)\eind{align*}$

voor … Deze vergelijking beschrijft de doorbuiging van de kolom voor elke waarde van de knikbelasting hierboven gedefinieerd. Alleen als de axiale belasting een van de waarden heeft die de vergelijking (eerder gedefinieerd) geeft…

$\begin{align*}P=\frac{n^2\pi^2EI}{L^2}\end{align*}$

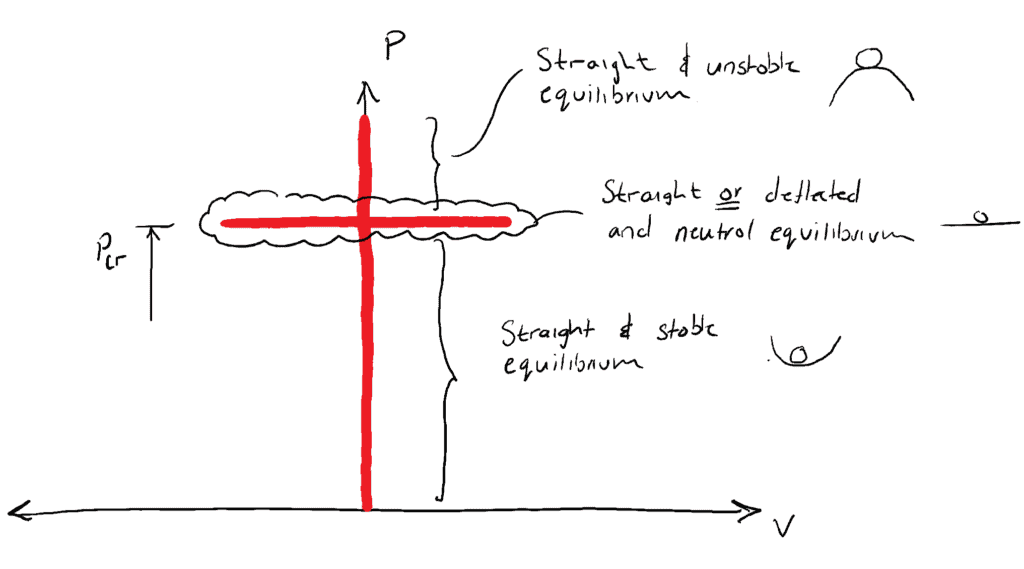
…kan de kolom een geknikte vorm hebben en in evenwicht zijn. Voor elke andere belasting zou de kolom recht zijn en in een toestand van STABIEL evenwicht $(PP_{cr})$ of ONSTABiel evenwicht $(PP_{cr})$ . We herinneren ons dit concept uit onze eerdere bespreking of geïdealiseerde kolomstructuren in de vorige post:

Maximale doorbuiging onder kritische belasting

Onze vergelijking voor de doorbuiging of geknikte vorm van een kolom bevat de parameter , overgebleven van onze algemene oplossing van de differentiaalvergelijking. We zien nu dat de grootte van de sinusgolf voorstelt of in deze context, de maximale laterale doorbuiging voor de afgebogen/geplooide doorbuiging (hierboven gedefinieerd):

$begin{align*}v(x)=C_1sinlinks(\frac{n\pi x}{L} \rechts)\eind{align*}$

Als we nu de evenwichtstoestanden in herinnering brengen, wanneer de kolom in zijn geknikte vorm $(P=P_{cr})$ en in een neutrale evenwichtstoestand is, kan de maximale laterale doorbuiging elke waarde hebben die nog voldoet aan onze kleine doorbuiging veronderstelling. We kunnen de waarde van grafisch weergeven…

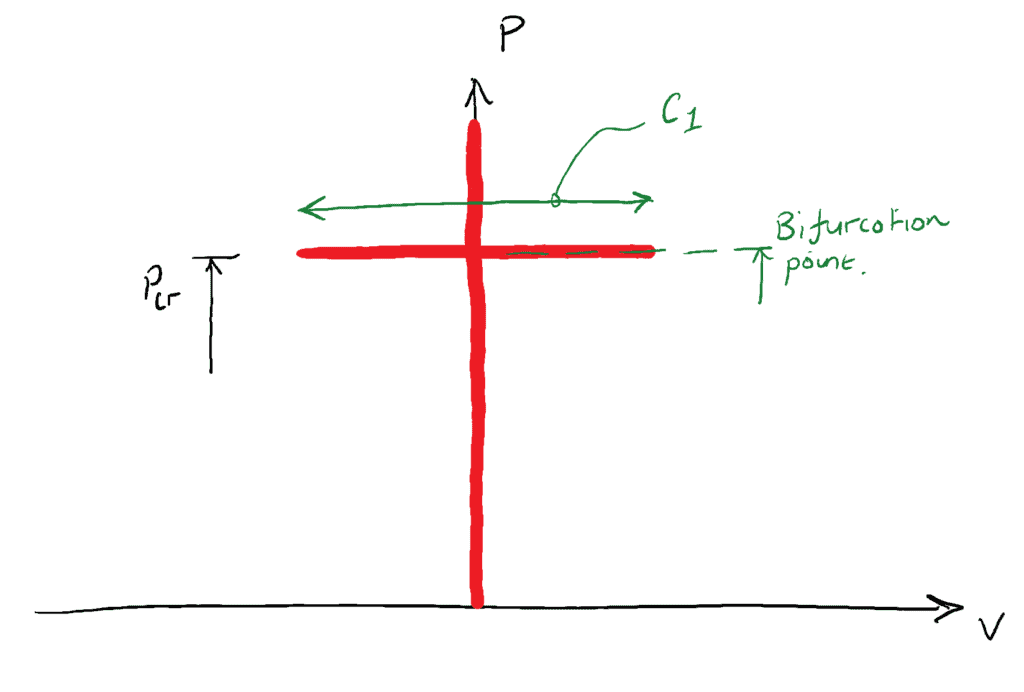
De waarde van is daarom mathematisch ongedefinieerd, het kan elke ‘kleine’ waarde hebben. Gelukkig levert dit geen praktische problemen op, zoals eerder gezegd is de toestand van neutraal evenwicht niet iets wat we in de civieltechnische praktijk waarnemen. Voor een civiel- of bouwkundig ingenieur wordt een kolom die $P_{cr}$ ondervindt, in principe als bezweken beschouwd. Deze theoretische neutrale evenwichtstoestand wordt ook wel een bifurcatiepunt genoemd.

Hogere orde knikmodes

Stel je een axiaal belaste vastgepinde eindkolom voor die op zijn middelste hoogte zijdelings wordt opgespannen (bijvoorbeeld door een vloerplaat). De kolom zou niet kunnen knikken onder de eerste kritische belasting (Euler knik) door de zijdelingse oplegging.

Door deze oplegging kan de kolom meer belasting dragen, totdat de tweede knikbelasting wordt bereikt . Aangezien de kolom niet tegen knikken in de tweede toestand wordt beperkt, zou hij nu knikken (of theoretisch in een neutrale evenwichtstoestand terechtkomen).

💡Een adequate zijdelingse beperking verhoogt de knikweerstand van een kolom door de mogelijkheid van knikken in lagere toestanden ‘af te sluiten’ en hogere knikbelastingen ‘vrij te geven’.

We kunnen de eerste drie knikmodes eenvoudig visualiseren door de belasting en de vervormingsvergelijkingen voor te evalueren.

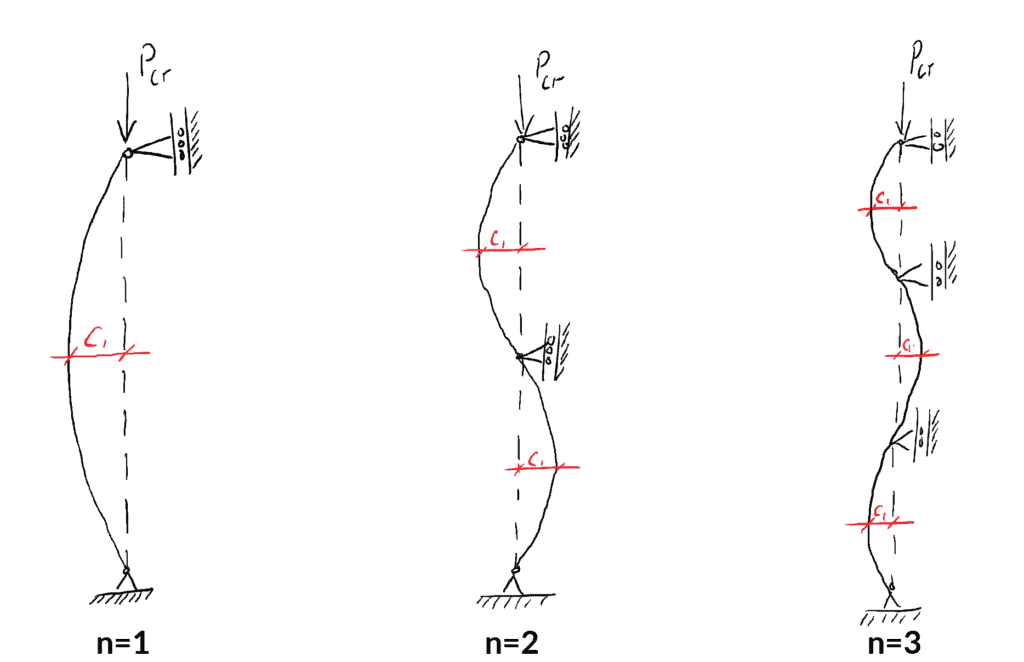
Mode

$\begin{align*}n=1\end{align*}$

$\begin{align*}n=2\end{align*}$

Kritische belasting

$>begin{align*}P_{cr} = \frac{\pi^2EI}{L^2}$

$>begin{align*}P_{cr} =$

Gebogen vorm

begin{align*}v(x) = C_1[sin]links(\frac{\pi x}{L}}rechts)\eind{align*}” class=”alignright”>

$begin{align*}v(x) = C_1sin-links(\frac{2pi x}{L}}rechts)\eind{align*}$

$begin{align*}v(x) = C_1}sinlinks(\frac{3pi x}{L}}rechts)$

📌 Voor elke gegeven modus, $P_{cr}$ de praktische bovengrens van de axiale belasting. Natuurlijke onvolkomenheden, bijvoorbeeld een kolom die uit het lood staat of een slechte uitlijning van de belasting, zullen vrijwel zeker leiden tot knikken wanneer de kritische belasting wordt overschreden.

3.0 Kolommen met andere ondersteuningscondities

Tot nu toe hebben we gekeken naar het gedrag van een kolom die aan beide uiteinden is vastgepind. Dit is het typische uitgangspunt. Maar hetzelfde proces kan worden gevolgd om de overeenkomstige vergelijkingen te bepalen voor kolommen met verschillende soorten ondersteuningscondities. In de onderstaande video’s zal ik de afleidingen uitvoeren om het proces te demonstreren voor:

Kolommen met een basis die tegen rotatie is bevestigd en vrij aan de top (fixed-free)
Kolommen die aan beide uiteinden tegen rotatie zijn bevestigd (fixed-fixed)
Kolommen die aan de basis tegen rotatie zijn bevestigd en aan de top zijn vastgepind (fixed-vast-vast)

Rotatievergelijking voor kolommen aan beide uiteinden vast-vast)

Rotatievergelijking voor kolommen onderaan vast-vast en bovenaan vrij (vast-vast)

ivvrij)

Rotatievergelijking voor kolommen die aan de onderzijde tegen rotatie worden gebogen en aan de bovenzijde worden vastgepind (vast-vastgepind)

Samenvatting ondersteuningsvoorwaarden

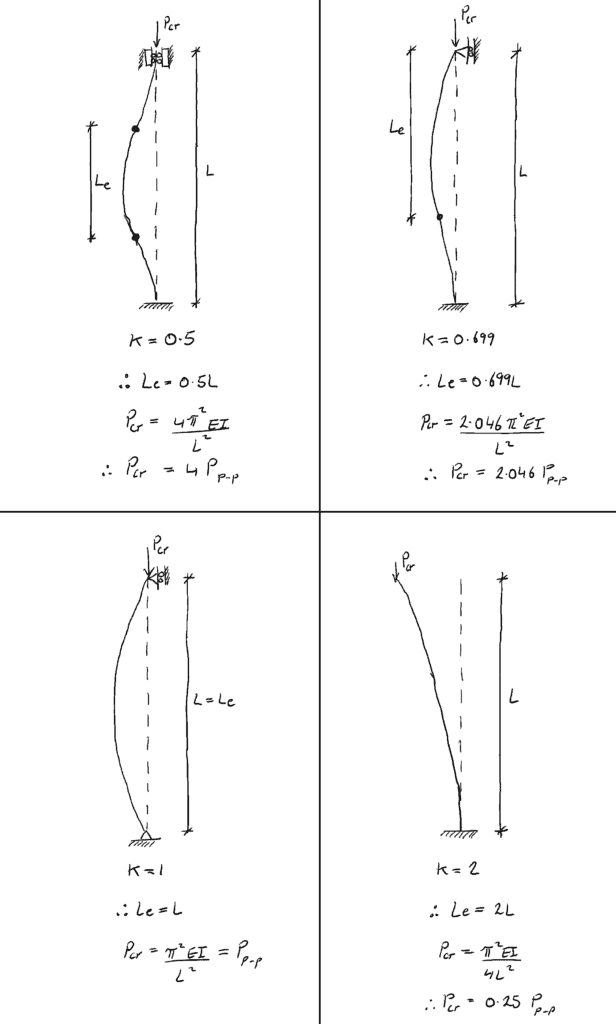
4.0 Knikas

We herinneren ons uit de vergelijking voor de knikbelasting dat deze een functie is van I, het tweede moment van de oppervlakte van de doorsnede:

$\begin{align*}P=\frac{n^2\pi^2EI}{L^2}\end{align*}$

Dus voor een gegeven doorsnede zal een kolom altijd knikken om de as met het lagere tweede moment van oppervlakte, de ‘zwakkere’ as. Hierbij wordt ervan uitgegaan dat beide assen evenveel spankracht hebben. Beschouw het geval van een universele kolomdoorsnede (UC) onder druk:

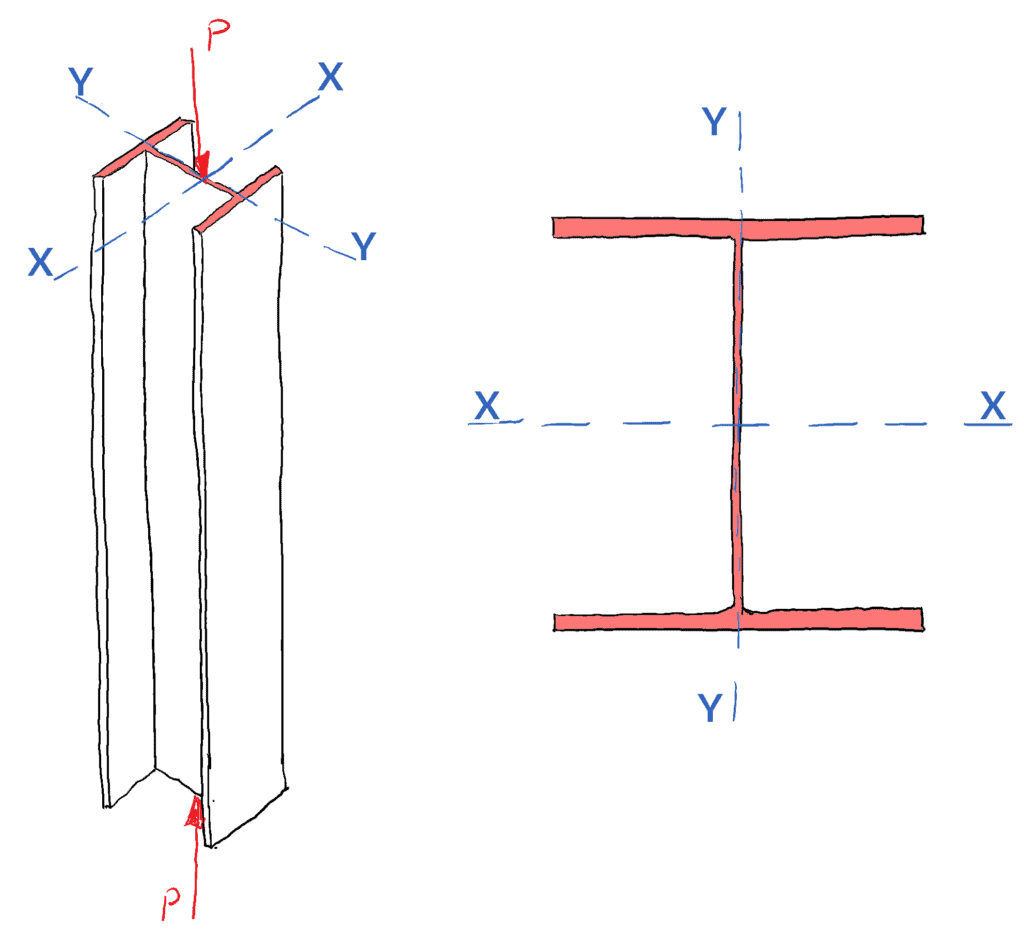
Aangezien de X-X-as, de hoofdas is (met de grootste waarde van het tweede oppervlaktemoment – u herinnert zich dit wellicht van uw studie van de cirkel van Mohr), is dit de sterkste as en zal de kolom dus eerst om de nevenprincipe- of Y-Y-as knikken.

Bij het bepalen van de knikbelasting voor een kolomconstructie speelt de vorm van de dwarsdoorsnede een sleutelrol, u moet de hoofd- en nevenprincipe-assen evalueren om de kritische knikas te bepalen.

5.0 Kritische Spanning

📌 De kritische spanning is de gemiddelde axiale spanning in een doorsnede onder de kritische belasting

doorsnede onder de kritische belasting

$\begin{align*}\sigma_{cr}=\frac{P_{cr}}{A}=\frac{\pi^2EI}{AL^2}\end{align*}$ $begin{align*}\sigma_{cr}=\frac{P_{cr}}{A}=\frac{\pi^2EI}{AL^2}$

We definiëren nu de kromtestraal, als:

$begin{align*}r=\sqrt{\frac{I}{A}}$

We kunnen de kritische spanning dus schrijven als:

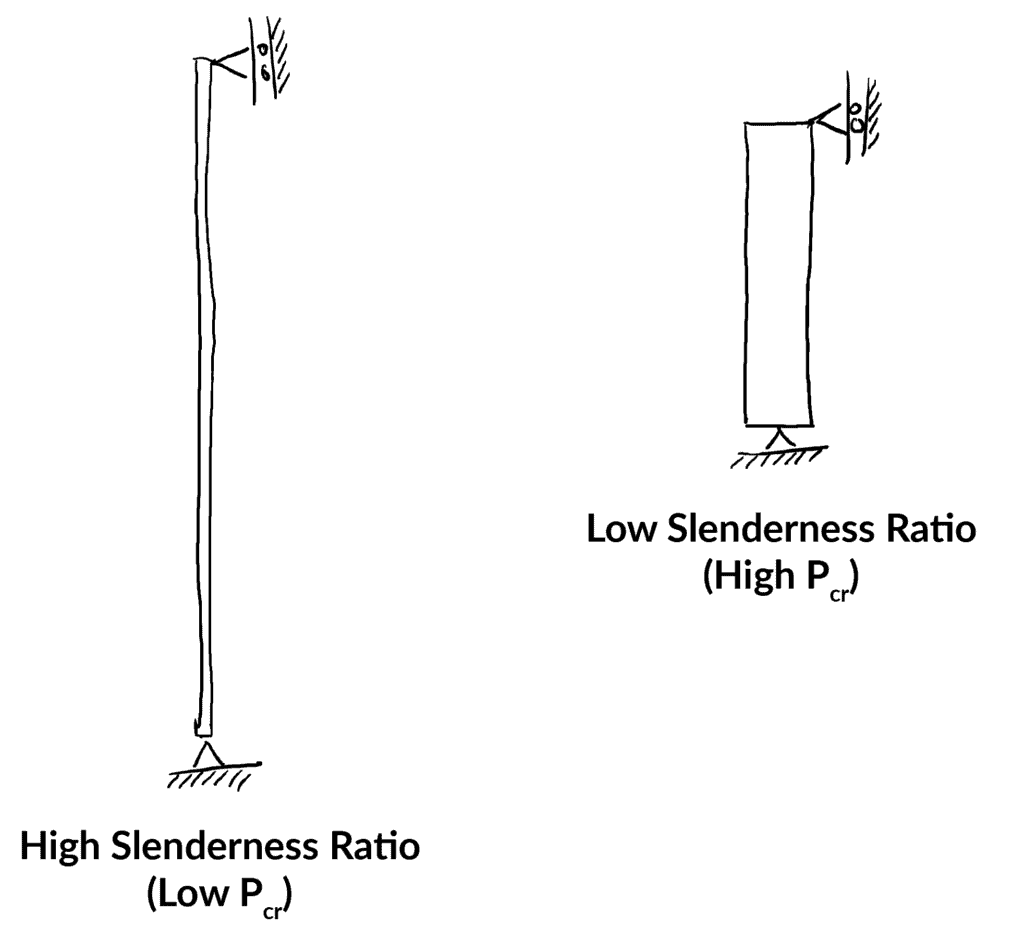
$\begin{align*}\sigma_{cr}=\frac{\pi^2E}{\left(\frac{L}{r}\right)^2}\end{align*}$ $\begin{align*}\sigma_{cr}=\frac{\pi^2E}{\left(\frac{L}{r}\right)^2}\end{align*}$

Tot slot definiëren we de Slenderness Ratio als:

$\begin{align*}\lambda=\frac{L}{r}\end{align*}$

De slankheidsverhouding is een zeer nuttige maatstaf voor de geometrie van een kolom en de gevoeligheid voor knikken. Een hoge slankheidsverhouding geeft aan dat de kolom gevoeliger is voor knikken. De slenderness ratio moet voor elke hoofdas afzonderlijk worden bepaald. We kunnen een intuïtie krijgen voor de slenderness ratio door beide uitersten te visualiseren,

De vergelijking voor de kritische spanning kan dus als functie van de slenderness ratio als volgt worden geschreven,

$\begin{align*}\sigma_{cr}=\frac{\pi^2E}{\lambda^2}\end{align*}$

Plotten van de kritische spanning versus de slankheidsverhouding voor een gegeven waarde van de elasticiteitsmodulus levert een Euler Curve op die het veilige bereik van de gemiddelde axiale spanning voor een gegeven buigverhouding aangeeft (of het veilige bereik van de waarden van de buigverhouding voor een gegeven axiale spanning),

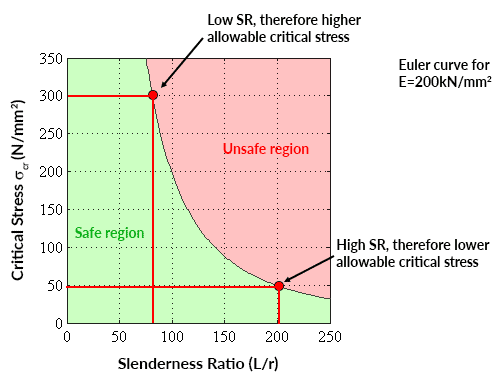
📌 Een Euler-kromme is alleen geldig voor kritische spanningen onder de vloeispanning van het materiaal

6.0 Kolom effectieve lengte

Het laatste begrip dat we in deze post zullen bekijken is de kolom effectieve lengte. De effectieve lengte van een kolom, , is de lengte tussen buigpunten op de afgebogen kromme/vorm (zelfs als de vorm moet worden verlengd tot een buigpunt is bereikt – hieronder besproken). Voor een kolom die aan beide uiteinden is vastgepind, is de effectieve lengte eenvoudigweg de volledige lengte van de kolom tussen de pinnen:

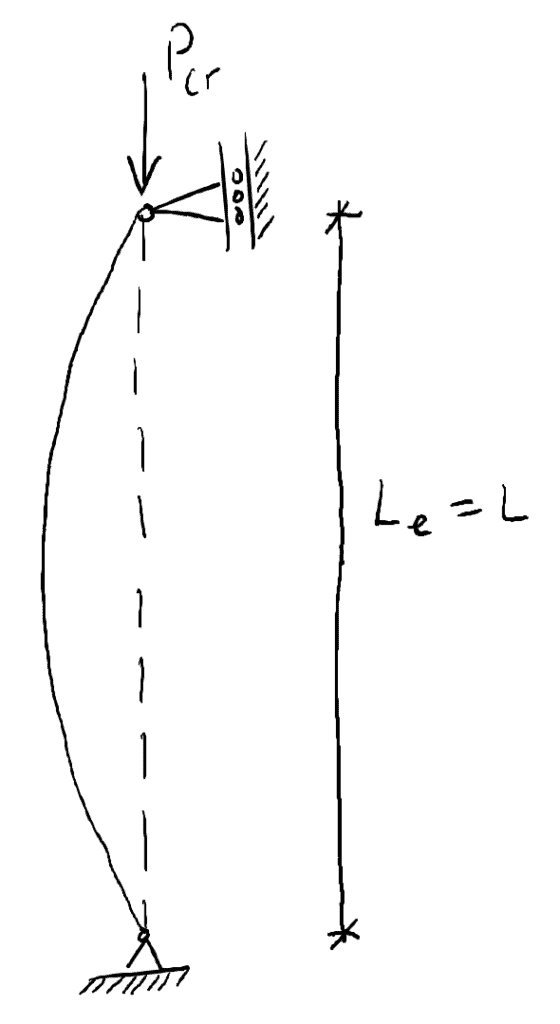
Beschouw een kolom met een vaste steun aan de basis en geen zijdelingse steun aan de top (vast-vrij). Aan de basis kan geen rotatie optreden. Om twee buigpunten op de afgebogen vorm te krijgen, moet deze worden verlengd…

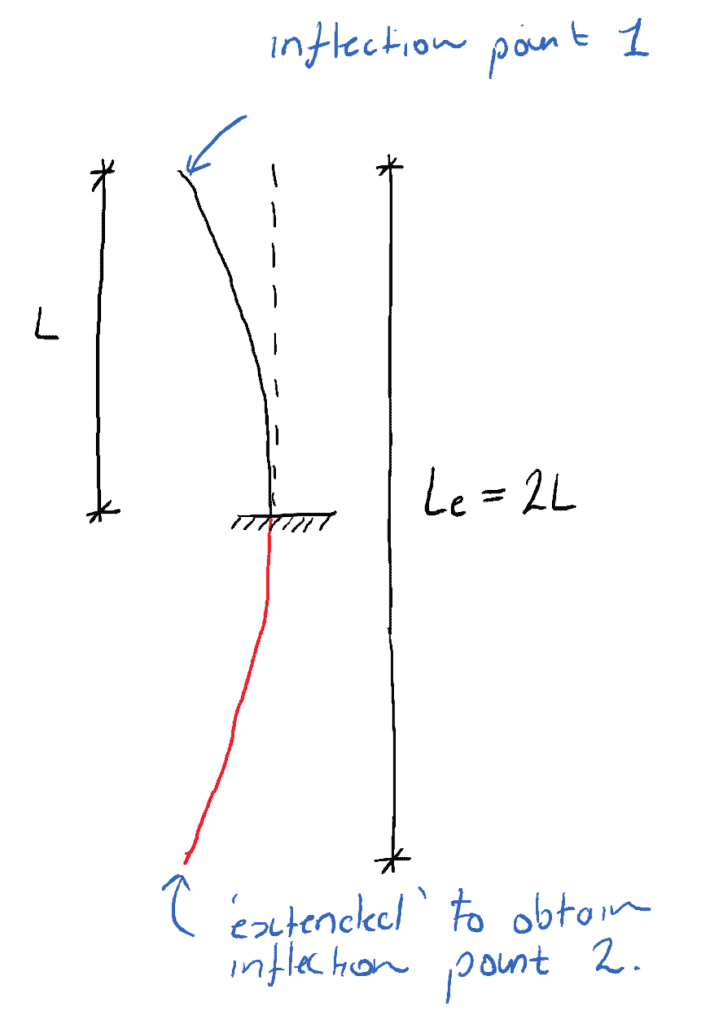
Het ‘denkbeeldige’ rode gedeelte van de afgebogen vorm is de verlenging die nodig is om buigpunt nummer 2 te krijgen. De effectieve lengte voor een kolom zonder vaste eindpunten is dus 2L.

📌 Een andere manier om over effectieve lengte te denken is dat het de lengte is van een equivalente kolom met een vastgepind eindpunt.

Voordat we onze discussie over effectieve lengte afsluiten, kunnen we een algemene uitdrukking voor de kritische belasting als volgt definiëren:

$\begin{align*}P_{cr}=\frac{\pi^2EI}{{L_e}^2}\end{align*}$

${align*}P_{cr}=\frac{\pi^2EI}{L_e}^2}{L_e}^2}$

Als we nu de Effectieve Lengte Factor introduceren, , zodanig dat , kunnen we de kritische belasting als functie van de effectieve lengtefactor stellen:

$begin{align*}P_{cr}=\frac{\pi^2EI}{(KL)}^2}$

Subscribe for Updates

Word op de hoogte gebracht wanneer nieuwe tutorials en cursussen

1.0 Knikvergelijking voor aan beide uiteinden vastgepinde kolommen

Opstellen van de differentiaalvergelijking

Oplossen van de differentiaalvergelijking

Oplossen voor de integratieconstanten

2.0 Knikmodes en modusvormen

Maximale doorbuiging onder kritische belasting

Hogere orde knikmodes

3.0 Kolommen met andere ondersteuningscondities

Rotatievergelijking voor kolommen aan beide uiteinden vast-vast)

Rotatievergelijking voor kolommen onderaan vast-vast en bovenaan vrij (vast-vast)

Rotatievergelijking voor kolommen onderaan vast-vast en bovenaan vrij (vast-vast)

Rotatievergelijking voor kolommen die aan de onderzijde tegen rotatie worden gebogen en aan de bovenzijde worden vastgepind (vast-vastgepind)

Samenvatting ondersteuningsvoorwaarden

4.0 Knikas

5.0 Kritische Spanning

6.0 Kolom effectieve lengte

Subscribe for Updates

Laat een antwoord achter Antwoord annuleren