Exponentiële functie vinden aan de hand van de grafiek – Exponentiële Functies

Wat zijn exponentiële functies?

Voordat we ons gaan bezighouden met exponentiële functies en de grafiek van exponentiële functies, laten we eerst eens kijken naar de algemene formule en theorie achter exponentiële functies.

Hieronder staat een van de meest algemene vormen van een exponentiële grafiek:

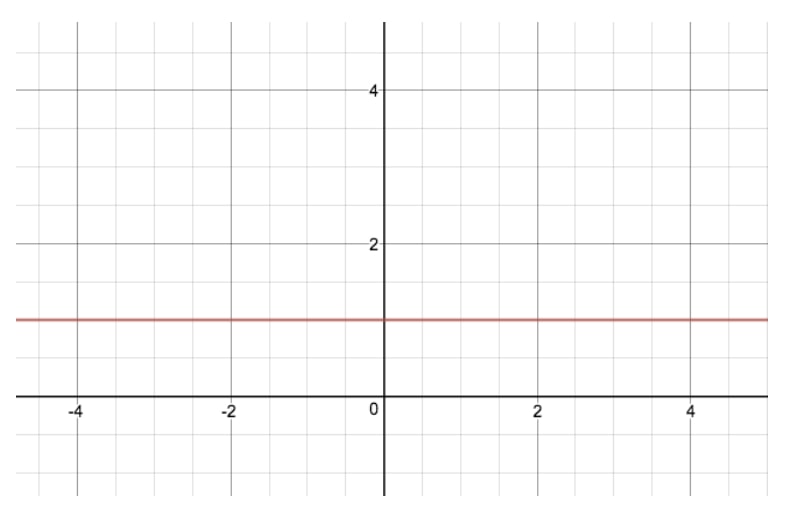
De exponentiële functievergelijking bij deze grafiek is y=2xy=2^xy=2x, en is de meest eenvoudige exponentiële grafiek die we kunnen maken. Als je je afvraagt hoe y=1xy=1^xy=1x eruit zou zien, hier is de exponentiële grafiek ervan:

Nu, wat betreft de reden waarom de grafieken van y=2xy=2^xy=2x en y=1xy=1^xy=1x zo verschillend zijn, is de beste manier om de theorie achter exponentiële functies te begrijpen een blik te werpen op een aantal tabellen.

Hierboven zie je drie tabellen voor drie verschillende “basiswaarden” – 1, 2 en 3 – die allemaal tot de macht van x zijn. Zoals je ziet, blijft voor exponentiële functies met een “basiswaarde” van 1, de waarde van y constant op 1, omdat 1 tot de macht van alles gewoon 1 is. Daarom is de bovenstaande grafiek van y=1xy=1^xy=1x gewoon een rechte lijn. In het geval van y=2xy=2^xy=2x en y=3xy=3^xy=3x (niet afgebeeld), daarentegen, zien we een steeds steiler wordende curve voor onze grafiek. Dat komt omdat naarmate x toeneemt, de waarde van y steeds groter wordt, of wat we “exponentieel” noemen.

Nu we een idee hebben hoe exponentiële vergelijkingen er in een grafiek uitzien, geven we de algemene formule voor exponentiële functies:

y=abd(x-c)+ky=ab^{d(x-c)}+ky=abd(x-c)+k

De bovenstaande formule is iets ingewikkelder dan eerdere functies waar je waarschijnlijk mee hebt gewerkt, dus laten we alle variabelen eens definiëren.

y – de waarde op de y-as

a – de verticale strek- of compressiefactor

b – de basiswaarde

x – de waarde op de x-as

c – de horizontale translatiefactor

d – de horizontale strek- of compressiefactor

k – de verticale translatiefactor

In deze les, zullen we alleen de basis van exponentiële functies behandelen, dus je hoeft je geen zorgen te maken over sommige van de bovenstaande variabelen. Maar, zodat je toegang hebt tot alle informatie die je nodig hebt over exponentiële functies en hoe je exponentiële functies grafisch kunt weergeven, laten we eens schetsen wat het veranderen van elk van deze variabelen doet met de grafiek van een exponentiële vergelijking.

1) Variabele “a”

Laten we de grafiek van y=2xy=2^xy=2x eens vergelijken met een andere exponentiële vergelijking waarbij we “a” wijzigen, waardoor we y=(-4)2xy=(-4)2^xy=(-4)2x

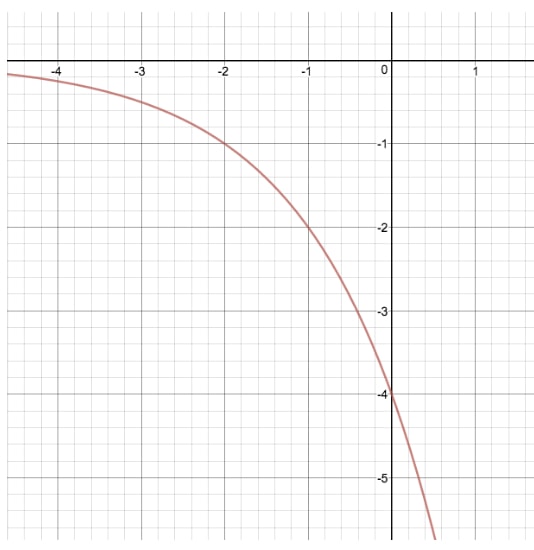
Door deze transformatie te maken, hebben we de oorspronkelijke grafiek van y=2xy=2^xy=2x zowel “uitgerekt” als “gereflecteerd” met zijn y-waarden. Om “a” te vinden door naar de grafiek te kijken, is het belangrijkste om op te merken dat wanneer x=0 en we geen waarde voor “k” hebben, het y-afsnijpunt van onze grafiek altijd gelijk zal zijn aan “a”.

2)Variabele “b”

Ook bekend als de “basiswaarde”, dit is eenvoudigweg het getal waar de exponent aan vast zit. Om het te vinden is algebra nodig, dat later in dit artikel zal worden besproken.

Variabele “c”

Laten we de grafiek van y=2xy=2^xy=2x eens vergelijken met een andere exponentiële vergelijking waarbij we “c” aanpassen, waardoor we y=2(x-2)y=2^{(x-2)}y=2(x-2)

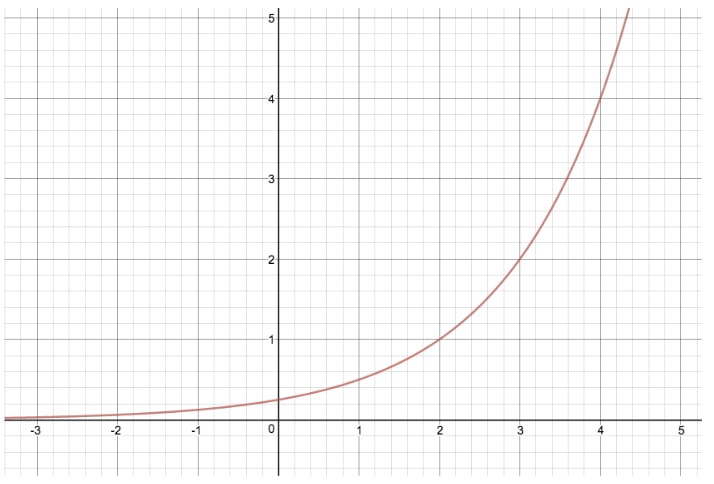
Door deze transformatie uit te voeren, hebben we de hele grafiek twee eenheden naar rechts verschoven. Als “c” gelijk was aan -2, zou de hele grafiek twee eenheden naar links zijn verschoven.

Variabele “d”

Laten we de grafiek van y=2xy=2^xy=2x eens vergelijken met een andere exponentiële vergelijking waarbij we “d” aanpassen, waardoor we y=24xy=2^{4x}y=24x

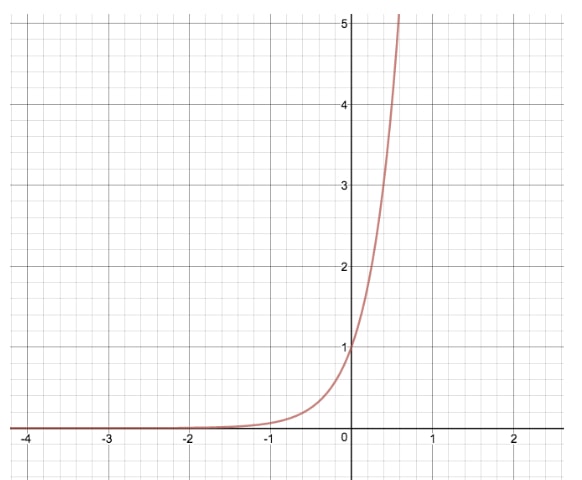
Door deze transformatie uit te voeren, hebben we de oorspronkelijke grafiek van y=2xy=2^xy=2x uitgerekt met zijn x-waarden, net zoals de variabele “a” de functie wijzigt met zijn y-waarden. Als “d” in dit voorbeeld negatief zou zijn, zou de exponentiële functie een horizontale afspiegeling ondergaan, in tegenstelling tot de verticale afspiegeling die we bij “a” zien.

Variabele “k”

Laten we de grafiek van y=2xy=2^xy=2x eens vergelijken met een andere exponentiële vergelijking waarbij we “k” aanpassen, waardoor we y=2x+2y=2^x+2y=2x+2

Door deze transformatie uit te voeren, hebben we de oorspronkelijke grafiek van y=2xy=2^xy=2x twee eenheden omhoog vertaald. Als “k” in dit voorbeeld negatief was geweest, zou de exponentiële functie twee eenheden naar beneden zijn vertaald. “k” is een bijzonder belangrijke variabele, want hij is ook gelijk aan wat we de horizontale asymptoot noemen! Een asymptoot is een waarde voor x of y die een functie benadert, maar nooit bereikt.

Neem bijvoorbeeld de functie y=2xy=2^xy=2x: voor deze exponentiële functie is k=0, en dus is de “horizontale asymptoot” gelijk aan 0. Dit is logisch, want welke waarde we ook invoeren voor x, we zullen y nooit gelijk krijgen aan 0. Voor onze andere functie y=2x+2y=2^x+2y=2x+2, is k=2, en dus is de horizontale asymptoot gelijk aan 2. Er is geen waarde voor x die we kunnen gebruiken om y=2 te maken.

En dat zijn alle variabelen! Nogmaals, sommige variabelen zijn ingewikkelder dan andere, dus het kost tijd om eraan te wennen met alle variabelen te werken en ze te vinden. Om meer te weten te komen over exponentiële functies en om vertrouwd te raken met de bovenstaande algemene vergelijking, bezoek dan deze uitstekende grafische rekenmachine website hier. Neem de tijd om met de variabelen te spelen, en krijg een beter gevoel voor hoe het veranderen van elk van de variabelen de aard van de functie beïnvloedt.

Nu, laten we aan de slag gaan.

Hoe vind ik exponentiële functies?

Hoe vind ik exponentiële functies?

Hoe vind ik exponentiële functies?

Het vinden van de vergelijking van exponentiële functies is vaak een proces dat uit meerdere stappen bestaat, en elk probleem is anders, afhankelijk van de informatie en het type grafiek dat we krijgen. Gegeven de grafiek van exponentiële functies, moeten we in staat zijn om sommige informatie uit de grafiek zelf te halen, en dan op te lossen voor de dingen die we niet direct uit de grafiek kunnen halen. Hieronder volgt een lijst van alle variabelen waarnaar we mogelijk moeten zoeken, en hoe we ze gewoonlijk vinden:

a – los het op met algebra, of het wordt gegeven

b – los het op met algebra, of het wordt gegeven

c – laat x = 0 en stel je voor dat “c” er niet is, dan is de waarde van y gelijk aan het y-afsnijpunt; tel nu hoeveel eenheden de y-waarde voor het y-afsnijpunt van de y-as af ligt, en dit zal gelijk zijn aan “c”

d – los het op met algebra

k – gelijk aan de waarde van de horizontale asymptoot

Natuurlijk zijn dit slechts de algemene stappen die je moet nemen om de exponentiële functievergelijking te vinden. De beste manier om te leren hoe je dit moet doen is door wat oefenopgaven te proberen!

Exponentiële Functies Voorbeelden:

Nu gaan we een paar voorbeelden proberen om alle theorie die we hebben behandeld in de praktijk te brengen. Met oefening zul je exponentiële functies met gemak kunnen vinden!

Voorbeeld 1:

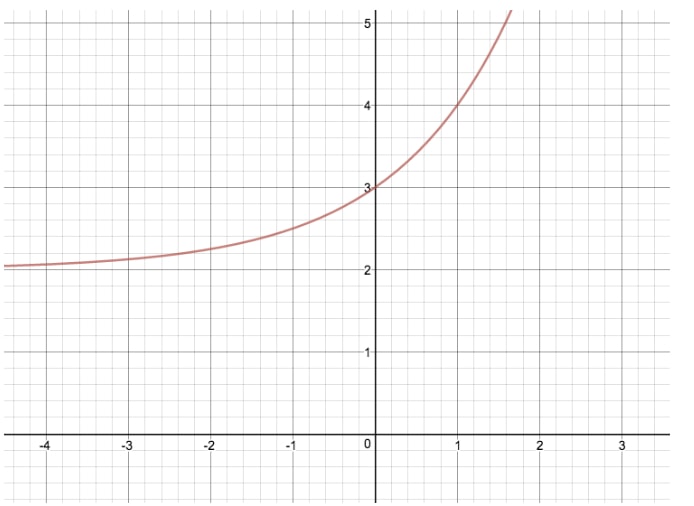
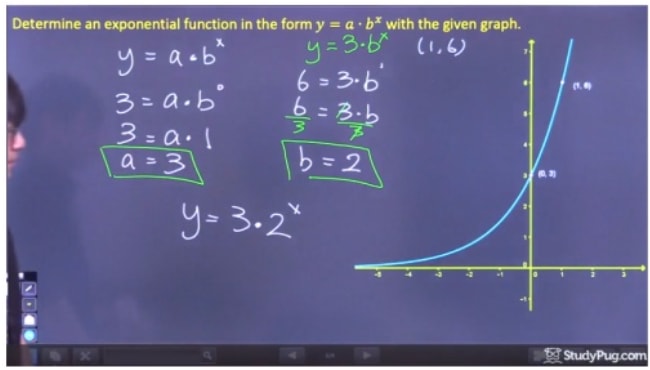
Bepaal de exponentiële functie in de vorm y=abxy=ab^xy=abx van de gegeven grafiek.

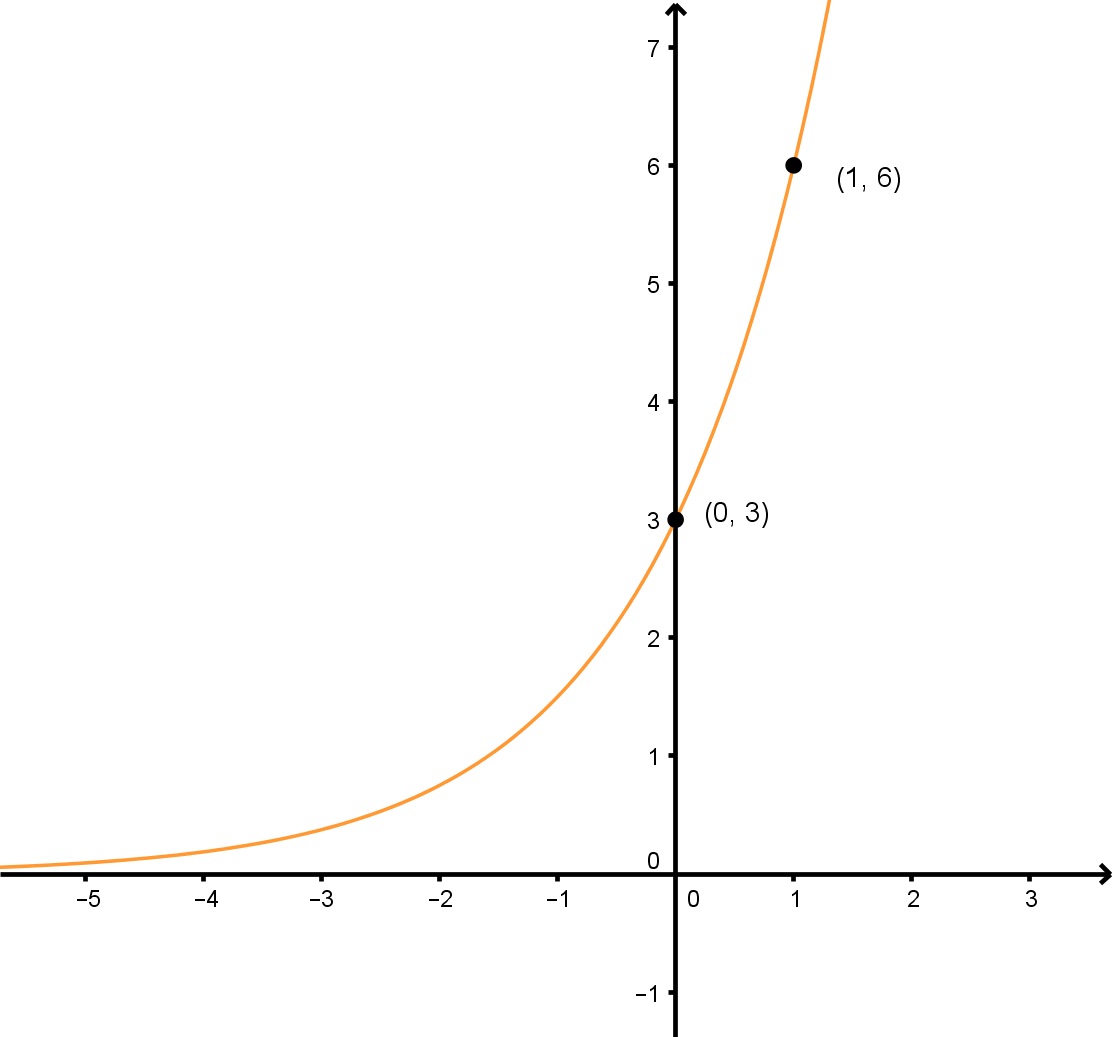
Om dit probleem op te lossen, moeten we de variabelen “a” en “b” vinden. Ook moeten we beide algebraïsch oplossen, omdat we ze niet uit de grafiek van de exponentiële functie zelf kunnen afleiden.

Stap 1: Los “a” op

Om “a” op te lossen moeten we een punt op de grafiek kiezen waar we bx kunnen elimineren, omdat we “b” nog niet kennen, en daarom moeten we het y-afsnijpunt (0,3) kiezen. Omdat b0 gelijk is aan 1, kunnen we vinden dat a=3. Omdat we geen waarde voor k hebben, is a als snelkoppeling gewoon gelijk aan het y-afsnijpunt van deze vergelijking.

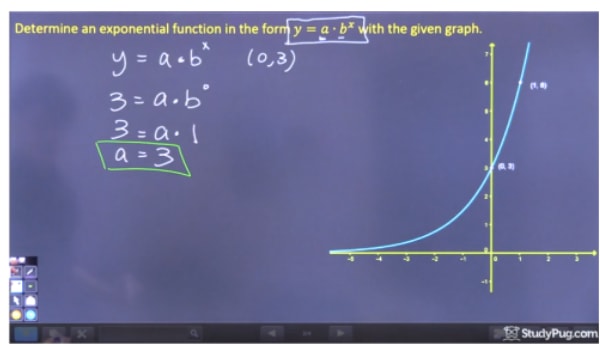
Step 2: Los op voor “b”

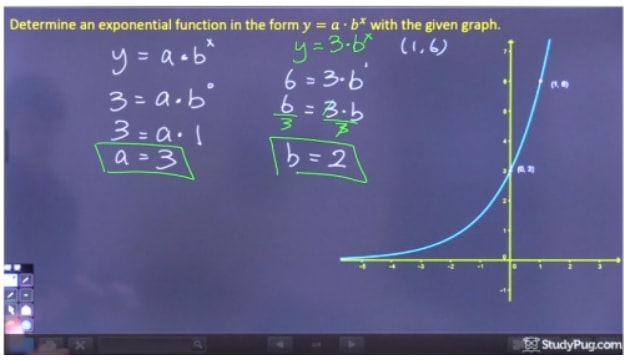
Step 3: Schrijf de uiteindelijke vergelijking

Voorbeeld 2:

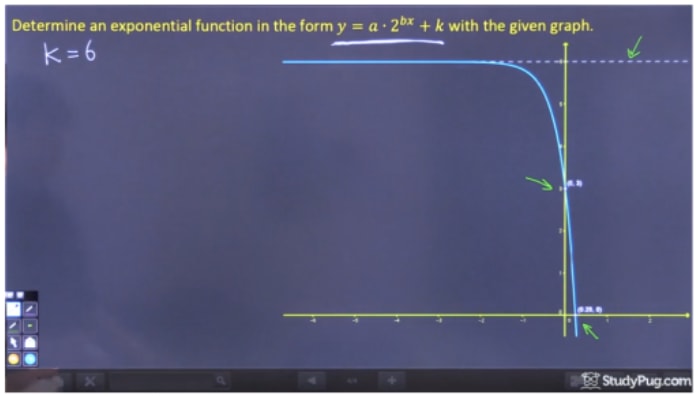
Bepaal de exponentiële functie in de vorm y=a2dx+ky=a2^{dx}+ky=a2dx+k van de gegeven grafiek.

Step 1: Vind “k” uit de grafiek

Om “k” te vinden, hoeven we alleen maar de horizontale asymptoot te vinden, en dat is duidelijk y=6. Daarom is k=6.

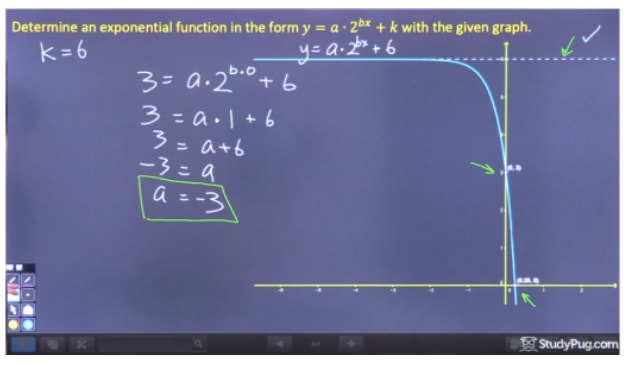
Step 2: Los op voor “a”

Step 3: Los op voor “b”

Step 4: Schrijf de laatste vergelijking

En dat is het voor exponentiële functies! Nogmaals, deze functies zijn iets complexer dan vergelijkingen voor lijnen of parabolen, dus zorg ervoor dat je veel oefenopgaven maakt om de nieuwe variabelen en technieken onder de knie te krijgen. Met meer oefening zullen exponentiële vergelijkingen en de grafieken van exponentiële functies binnenkort geen moeite meer kosten!