Factorial

Wat is Factorial?

De factorial (aangeduid of voorgesteld als n!) voor een positief getal of geheel getal (dat wordt aangeduid met n) is het product van alle positieve getallen die voorafgaan aan of equivalent zijn met n (het positieve gehele getal). De factoriële functie komt voor in verschillende gebieden van de wiskunde, waaronder algebra, wiskundige analyse, en combinatoriek.

Begonnen in de jaren 1200, werden factorials gebruikt om permutaties te tellen. De notatie voor een factorial (n!) werd begin 1800 geïntroduceerd door Christian Kramp, een Franse wiskundige.

De factorialformule is hieronder te zien:

definitie van de Factorial

De functie van een factorial wordt gedefinieerd door het product van alle positieve gehele getallen vóór en/of gelijk aan n, dat is:

n! = 1 ∙ 2 ∙ 3 ∙∙∙∙ (n-2) ∙ (n -1) ∙ n,

wanneer we kijken naar waarden of gehele getallen groter dan of gelijk aan 1. Het kan dan worden geschreven als:

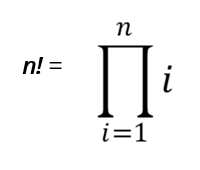
De bovenstaande vergelijking wordt geschreven volgens de pi product notatie, en resulteert in de terugkerende relatie die hieronder te zien is:

n! = n ∙ (n – 1) !.

Een aantal voorbeelden van de notatie is hieronder te zien:

• 4! = 4 ∙ 3!
• 7! = 7 ∙ 6!
• 80! = 80 ∙ 79!, enz.

Factorialentabel

De onderstaande tabel geeft een overzicht van de factorialen voor gehele getallen tussen 0 en 10:

Factorie van 0 (nul)

Het is algemeen bekend dat de factorie van 0 gelijk is aan 1 (één). Deze kan worden weergegeven als:

0! = 1

Er zijn verschillende redenen om de bovenstaande notatie en definitie te rechtvaardigen. Ten eerste maakt de definitie een compacte uitdrukking mogelijk van een aanzienlijk aantal formules, waaronder de exponentiële functie, en creëert de definitie een uitbreiding van het recurrente verband tot 0.

Daarnaast omvat de definitie van de nulfactorie (n!), wanneer n = 0, het product van geen getallen, wat betekent dat het equivalent is met de vermenigvuldigingsidentiteit in bredere zin.

Daarnaast omvat de definitie van de nulfactorie slechts één permutatie van nul of geen objecten. Tenslotte valideert de definitie ook een aantal identiteiten in de combinatoriek.

Op te merken definities met betrekking tot de nulfactoriaal

• Combinatoriek: Een gebied in de wiskunde dat zich richt op tellen.
• Permutatie: In de wiskunde verwijst permutatie naar de rangschikking van de leden van een verzameling in een lineaire volgorde of opeenvolging.
• Recurrence relation: Recurrence relatie, in de wiskunde, verwijst naar een vergelijking die een opeenvolging of uitgebreide reeks van waarden, recursief definieert. Recursie betekent iets definiëren in termen van zichzelf.

Verschillende toepassingen voor de Factorische Functie

De Factorische Functie kan in verschillende gebieden van de wiskunde worden gevonden. Ten eerste zijn er n! onderscheiden manieren om n specifieke voorwerpen in een reeks te rangschikken. Ook kunnen factorialen worden gebruikt om de onwetendheid of veronachtzaming van ordening in een formule te verklaren, door als noemer te dienen.

Factorialen komen ook voor in algebra via de binomiale stelling en in calculus, waar ze voorkomen in de noemers van de formule van Taylor. Verder komt een factorie voor in de waarschijnlijkheids- en getaltheorieën en kunnen ze worden gebruikt om uitdrukkingen te manipuleren.

Andere reeksen vergelijkbaar met de factorie

In de wiskunde zijn er een aantal reeksen die vergelijkbaar zijn met de factorie. Hiertoe behoren:

• Dubbele Factorialen, die worden gebruikt om goniometrische integralen te vereenvoudigen.
• Multi-factorialen, die met meerdere uitroeptekens kunnen worden aangeduid.
• Primorialen, waarbij het product wordt verkregen van de priemgetallen, die kleiner zijn dan of gelijk aan n.
• Super-factorialen, die gedefinieerd worden als het product van de eerste n factorialen.
• Hyper-factorialen, die het resultaat zijn van de vermenigvuldiging van een aantal opeenvolgende waarden, gaande van 1 tot n.

Aanvullende bronnen

CFI is de officiële leverancier van de wereldwijde Commercial Banking & Credit Analyst (CBCA)™CBCA™-certificeringDe Commercial Banking & Credit Analyst (CBCA)™-accreditatie is een wereldwijde standaard voor kredietanalisten die betrekking heeft op financiën, boekhouding, kredietanalyse, kasstroomanalyse, convenantmodellering, aflossing van leningen, en meer. certificeringsprogramma, ontworpen om iedereen te helpen een financieel analist van wereldklasse te worden. Om uw carrière vooruit te helpen, zullen de aanvullende CFI-bronnen hieronder nuttig zijn:

• CorrelatiematrixCorrelatiematrixEen correlatiematrix is eenvoudigweg een tabel die de correlatiecoëfficiënten voor verschillende variabelen weergeeft. De matrix geeft de correlatie weer tussen alle mogelijke paren van waarden in een tabel. Het is een krachtig instrument om een grote dataset samen te vatten en patronen in de gegeven gegevens te identificeren en te visualiseren.
• Financiële wiskundeFinanciële wiskunde beschrijft de toepassing van wiskunde en wiskundige modellering om financiële problemen op te lossen. het wordt soms aangeduid als
• QuantsQuantitatieve analisten (ook wel “quants” genoemd) zijn professionals die gespecialiseerd zijn in het ontwerpen, ontwikkelen en implementeren van algoritmen en wiskundige of statistische modellen die bedoeld zijn om complexe financiële problemen op te lossen. In hun werk passen kwantitatieve analisten een mix van technieken en kennis toe
• StandaardverdelingBemonsteringsverdelingEen monsternemingsverdeling verwijst naar een waarschijnlijkheidsverdeling van een statistiek die ontstaat uit het kiezen van willekeurige steekproeven uit een gegeven populatie