Handige SAT wiskunde formules

Eén van de eerste dingen die je moet doen als je studeert voor het wiskunde gedeelte van de SAT is formules in je geheugen vastleggen. Als je niet zeker weet waar je moet beginnen, zal deze lijst je helpen.

Hier zijn 9 SAT wiskunde formules die je zullen helpen bij het maken van de test. Gebruik deze lijst als een begin.

Leer hoe je je kunt voorbereiden op gestandaardiseerde tests met onze voorbereidingscursussen voor SAT en ACT het hele jaar door.

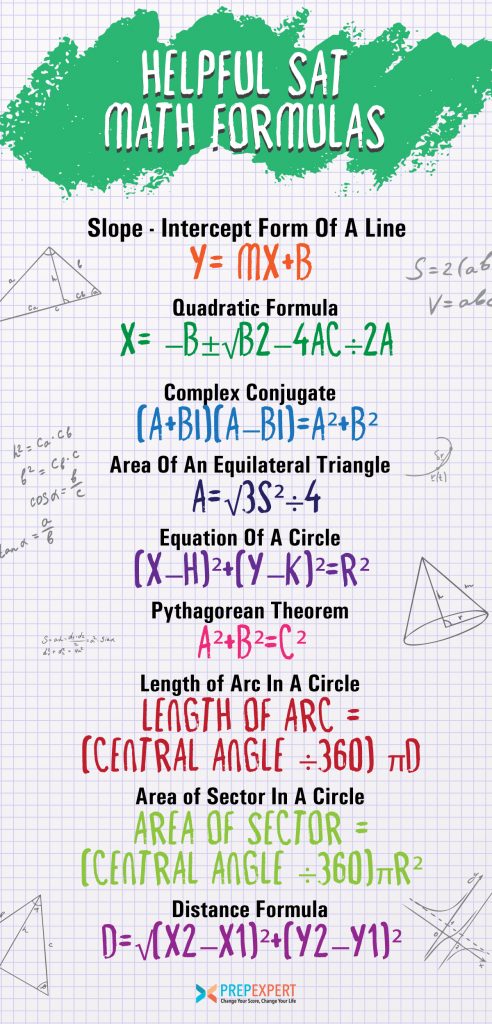
Slope-Intercept Form Of A Line

y=mx+b

“m” staat voor de helling van de vergelijking, “b” voor de y-waarde van het y-afsnijpunt. Bijvoorbeeld, als we de vergelijking y=3x+5 hebben, dan is de helling ‘3’ en het y-afsnijpunt (0,5).

Kwadratische formule

x=-b±√b2-4ac÷2a

Met deze formule kun je de wortels van een kwadratische vergelijking vinden als deze niet gemakkelijk in factoren te ontbinden is. De kwadratische vergelijking moet echter de vorm hebben van y=ax2+bx+c.

Op dat punt moet je de coëfficiënten en constanten in de formule invoeren. Vergeet niet dat je, vanwege de ± in de teller, twee aparte antwoorden krijgt.

Complex Conjugate

(a+bi)(a-bi)=a²+b²

De meeste SAT wiskunde-examens bevatten ten minste één vraag waarin je met imaginaire getallen moet omgaan. Met de complex-conjugaatformule kun je het imaginaire deel van een complex getal wegstrepen. Het resultaat is dat je een reëel getal overhoudt.

Area Of An Equilateral Triangle

A=√3s²÷4

De formule voor de oppervlakte van een regelmatige driehoek wordt normaal gesproken gegeven op het naslagblad van de toets, maar je moet wel de hoogte van de driehoek weten. Soms wordt je de hoogte niet gegeven en moet je het zelf uitzoeken.

Het goede nieuws is dat je de oppervlakte van een gelijkzijdige driehoek kunt berekenen door de lengte van een van de zijden in deze formule in te vullen.

Vergelijking van een cirkel

(x-h)²+(y-k)²=r²

Normaal zal een SAT wiskundevraag het gebruik van de vergelijking van een cirkel vereisen. In deze vergelijking stellen de variabelen h en k de coördinaten voor het middelpunt van de cirkel voor en r
de straal van de cirkel.

De stelling van Pythagoras

a²+b²=c²

De stelling van Pythagoras geldt voor regelmatige rechthoekige driehoeken. Het doel is om je in staat te stellen een van de onbekende zijlengtes op te lossen gegeven een andere zijlengte. a en b zijn de benen van de driehoek, en c is de schuine zijde.

Lengte van boog in een cirkel

lengte van boog = (centrale hoek ÷360) πd

Geometrie vragen komen niet vaak voor in het SAT wiskunde gedeelte, maar je zult waarschijnlijk nog wel een vraag krijgen die vraagt naar bogen of sectoren in een cirkel. Een cirkelboog is een lengte tussen twee punten op een cirkel.

Ze worden meestal gemeten door twee stralen vanuit het middelpunt van de cirkel te verlengen met een hoek tussen hen gevormd. Je kunt de graad van die boog als fractie van 360 gebruiken en dan vermenigvuldigen met de vergelijking voor de omtrek om de booglengte te vinden.

Area of Sector In A Circle

area of sector = (centrale hoek ÷360)πr²

Niet anders dan een boog, is de sector van een cirkel het gebied tussen twee stralen die zich vanuit het middelpunt uitstrekken. Zie het visueel eigenlijk als een stuk taart. Nogmaals, vermenigvuldig de maat van de graad als een breuk van 360 en vermenigvuldig het dan met de vergelijking voor de oppervlakte van een cirkel om de oppervlakte van de sector te vinden.

Afstandsformule

d=√(x2-x1)²+(y2-y1)²

De afstandsformule is fantastisch om snel de afstand tussen twee punten te bepalen. Om hem te gebruiken, neem je gewoon de waarden van de coördinaten en voer je ze in om de afstand te vinden. en zorg ervoor dat je de kwadraten en de vierkantswortel in de juiste stap toepast.

Voor meer teststrategie, college toelatingen, en studiebeurs applicatie tips schrijf je je in voor onze GRATIS les die nu plaatsvindt!