Matrix Inversie: De Inverse van een Matrix vinden

Keer terug naar de Lessenindex | Doe de lessen op volgorde | Printvriendelijke pagina

Matrix Inversie:
De inverse van een matrix vinden (pagina 1 van 2)

Voor matrices bestaat er niet zoiets als delen. Je kunt matrices optellen, aftrekken en vermenigvuldigen, maar je kunt ze niet delen. Er is wel een verwant concept, dat “inversie” wordt genoemd. Eerst zal ik bespreken waarom inversie nuttig is, en daarna zal ik laten zien hoe je het moet doen.

Denk terug aan toen je voor het eerst leerde hoe je lineaire vergelijkingen moest oplossen. Als je iets kreeg als “3x = 6”, dan zou je dat oplossen door beide kanten te delen door 3. Omdat vermenigvuldigen met 1/3 hetzelfde is als delen door 3, zou je ook beide kanten kunnen vermenigvuldigen met 1/3 om hetzelfde antwoord te krijgen: x = 2. Als je iets moest oplossen als “(3/2)x = 6”, dan zou je nog steeds beide kanten kunnen delen door 3/2, maar het was waarschijnlijk gemakkelijker om beide kanten te vermenigvuldigen met 2/3. De reciproke breuk 2/3 is de inverse van 3/2, want als je de twee breuken vermenigvuldigt, krijg je 1, wat in deze context “de (vermenigvuldigende) identiteit” wordt genoemd: 1 wordt de identiteit genoemd omdat iets met 1 vermenigvuldigen de waarde ervan niet verandert.

Deze terminologie en deze feiten zijn heel belangrijk voor matrices. Als je een matrixvergelijking krijgt zoals AX = C, waarbij je A en C krijgt en X moet uitrekenen, zou je de matrix A willen “delen”. Maar je kunt niet delen met matrices. Maar wat als je de inverse van A zou kunnen vinden, vergelijkbaar met het vinden van de reciproke breuk hierboven? Met de inverse van A, geschreven als “A-1” en uitgesproken als “A inverse”, zou je de A uit de matrixvergelijking kunnen weglaten en dan X kunnen oplossen.

AX = C
A-1AX = A-1C
IX = A-1C
X = A-1C

Hoe is “A-1AX” aan de linkerkant van de vergelijking veranderd in “X”? Denk eens terug aan de aard van omkeringen voor gewone getallen. Als je een getal (zoals 3/2) en zijn inverse (in dit geval, 2/3) met elkaar vermenigvuldigt, krijg je 1. En 1 is de identiteit, zo genoemd omdat 1x = x voor elk getal x. Het werkt op dezelfde manier voor matrices. Als je een matrix (zoals A) vermenigvuldigt met zijn inverse (in dit geval,
A-1), dan krijg je de eenheidsmatrix I. En het punt van de identiteitsmatrix is dat IX = X voor elke matrix X (dat wil zeggen “elke matrix van de juiste grootte”, natuurlijk).

Het moet worden opgemerkt dat de volgorde in de vermenigvuldiging hierboven belangrijk is en helemaal niet willekeurig is. Bedenk dat voor matrices de vermenigvuldiging niet commutatief is. Dat wil zeggen, AB is bijna nooit gelijk aan BA. De matrixvergelijking “links” vermenigvuldigen (om A-1AX te krijgen) is dus helemaal niet hetzelfde als “rechts” vermenigvuldigen (om AXA-1 te krijgen). En je kunt niet zeggen dat het product AXA-1 gelijk is aan A-1AX, want je kunt de volgorde in de vermenigvuldiging niet omwisselen. In plaats daarvan moet je A-1 aan de linkerkant vermenigvuldigen, dus direct naast de A in de oorspronkelijke matrixvergelijking. En aangezien je bij het oplossen hetzelfde moet doen met beide kanten van een vergelijking, moet je ook aan de rechterkant van de vergelijking “links” vermenigvuldigen, wat resulteert in A-1C. Je mag niet nonchalant zijn met het plaatsen van de matrices; je moet precies, correct en consequent zijn. Dit is de enige manier om A te annuleren en de matrixvergelijking op te lossen.

Zoals je hierboven hebt gezien, kunnen inverse matrices erg nuttig zijn voor het oplossen van matrixvergelijkingen. Maar, gegeven een matrix, hoe inverteer je die? Hoe vind je de inverse? De techniek om matrices te inverteren is nogal slim. Voor een gegeven matrix A en zijn inverse A-1, weten we dat we A-1A = I. We gaan de eenheidsmatrix I gebruiken in het proces voor het inverteren van een matrix.

• Vind de inverse van de volgende matrix.

Eerst schrijf ik de ingangen de matrix A op, maar ik schrijf ze in een dubbelbrede matrix:

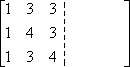
In de andere helft van de dubbele-brede schrijf ik de identiteitsmatrix:

Nu ga ik matrix-rijbewerkingen uitvoeren om de linkerhelft van de dubbelbrede om te zetten in de identiteit. (Zoals altijd bij rij-operaties is er niet één “juiste” manier om dit te doen. Wat volgt zijn gewoon de stappen die toevallig bij me opkwamen. Uw berekeningen kunnen er heel anders uitzien.)

Nu het linkerlid van de dubbele-breedte de identiteit bevat, bevat het rechterlid de inverse. Dat wil zeggen, de inverse matrix is de volgende:

Merk op dat we kunnen bevestigen dat deze matrix de inverse is van A door de twee matrices te vermenigvuldigen en te bevestigen dat we de identiteit krijgen: Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved

Let op: in het “echte leven” is de inverse zelden een matrix gevuld met keurige hele getallen zoals deze. Maar met een beetje geluk, vooral als je inversen met de hand doet, krijg je mooie matrices zoals deze om te doen.

Top | 1 | 2 | Terug naar index Volgende >>