Wat is het grootste getal?

Tallen gaan oneindig door – maar op weg naar oneindigheid zijn er een paar behoorlijk verre tussenposten.

Voor onze voorouders was een miljoen zo groot als getallen hoefden te worden. Het was niet nodig zich te beroepen op de miljarden (1.000.000.000) van de financiële wereld of de terabytes (1012) van de informatica. Technologie heeft ons blasé gemaakt over het gebruik van 9- of 12-cijferige getallen in gesprekken. Er is echter nog een lange weg te gaan voordat we zelfs maar de schaal van onze plaats in het heelal hebben ingehaald, laat staan de duizelingwekkend gigantische getallen die wiskundigen hebben bedacht.

Standaardgetallen

Meer dan een miljard – de orde van grootte van de menselijke bevolking – moeten we echt afscheid nemen van het idee om namen voor getallen te hebben. (Hoewel ze wel bestaan tot 1063, zijn ze niet algemeen in gebruik). Voor de afstand die het licht in een minuut aflegt, het aantal atomen in een gram koolstof, of de afstand tussen sterrenstelsels, gebruiken wetenschappers de standaardvorm om zich uit te drukken. De standaardvorm slaat alle getallen op in het formaat a × 10n, waarbij a een getal tussen 1 en 10 is en n een willekeurig getal kan zijn. Het is wat je zou gebruiken om te praten over het aantal koolstofatomen in een 12g monster. Wat overigens 6,22 x 1023 is, Avogadro’s getal, en behoorlijk groot. Het waarneembare heelal is ongeveer 8,8 × 1023 km breed, en er zijn naar schatting 1087 deeltjes in. Maar veel groter dan deze getallen zijn de constructies van wiskundige geesten.

Laat me googol it for you

Immortalised in common usage by the internet giant, a googol is the number 10100 – 10, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000. De Amerikaanse wiskundige Edward Kasner vroeg zijn neef Milton om het getal een naam te geven, en het werd een googol. Maar het volgende echt grote getal is het googolplex, dat 10 tot de macht van een googol verheft. Dit is astronomisch veel groter dan een googol – het is onmogelijk om een googolplex in standaardnotatie op te schrijven, zelfs als je op elk deeltje in het heelal een enkel cijfer zou schrijven.

De macht der machten

Door een exponentieel in de exponent op te nemen, worden getallen echt sneller groter.

3×3×3=27

3(33) = 7.625.597.484.987

Natuurlijk zou men, op zoek naar grotere getallen, meer en meer machten aan de toren toevoegen. Dit wordt echter al snel onhandig om op te schrijven, en resulteert in torens die die van Pisa stabiel doen lijken. Verandering van notatie maakt het mogelijk deze torens samen te vatten en hogere concepten uit te drukken.

Volg de pijlen

Ontwikkelen van een andere manier om machten aan te duiden:

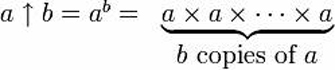
Donald Knuth bedacht een nieuwe operator voor herhaalde exponentiatie (“tetration”), om die krachttorens met beide benen op de grond te zetten.

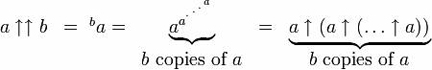
In het gebruik ziet de dubbele pijl er als volgt uit:

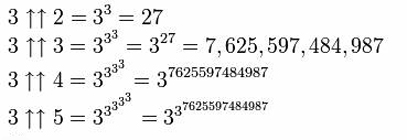
Dit kan nog verder worden uitgebreid door een derde pijl toe te voegen, waardoor de operatie van ‘pentation’ – herhaalde tetratie – ontstaat.

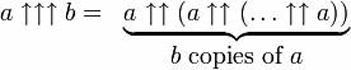
In woorden komt dat neer op het tetreren van a tot a (dus een machttoren van a’s), dan het bouwen van nog een toren van a’s even hoog als die machttoren, dan het resultaat van die toren gebruiken om het aantal a’s in de volgende toren te bepalen – resulterend in het berekenen van b torens, die in hoogte toenemen volgens het resultaat van de vorige tetratie.

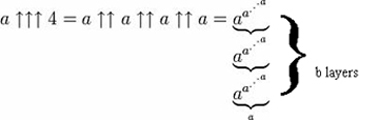
En er kunnen nog meer pijlen worden toegevoegd, hoewel het nadenken over de operaties die ze aanduiden meer hersentijd kan vergen dan je bereid bent aan de kwestie te wijden. Maar gewapend met deze notatie kunnen we nu enkele echt grote getallen erkennen.

Bellen met Ackermann en Graham

Wiskundige bewijzen hebben ons enkele enorme hoeveelheden opgeleverd. Aan het begin van de twintigste eeuw wilden wiskundigen weten hoe ze konden bepalen of een rij berekenbaar was – kon er een mechanisch proces worden gedefinieerd om die rij uit te werken? Men stelde voor dat een rij berekenbaar was als hij de eigenschap had “primitief recursief” te zijn. Wilhelm Ackermann gooide roet in het eten door een reeks te bedenken die weliswaar berekenbaar was, maar niet primitief recursief. En die gaat als volgt:

Start met de eenvoudigst mogelijke wiskundige bewerking – optellen. Pas dit toe op het eerste natuurlijke getal, 1:

1 + 1 = 2

Ga dan naar de volgende bewerking, vermenigvuldiging (herhaalde optelling). Doe dit met het volgende getal:

2 × 2 = 4

De volgende bewerking is herhaalde vermenigvuldiging – exponentiëren voor jou en mij – met 3 als variabele.

33 = 27

Zo ver, zo nietig. Maar we hebben net een functie gedefinieerd voor herhaald exponentiëren, tetreren, en als we dit doen tot 4..

Het ziet er klein uit, heeft 10154 cijfers. En dit is nog maar de 4e term in de reeks.

De vijfde is … een machtstoren van vijf cijfers hoog.

Zesde is . Slechts vijf symbolen geven een getal aan dat groter is dan er plaats voor is in het heelal, zelfs als je elk cijfer in een lettertype van 1 nm breed zou schrijven. En de reeks gaat maar door.

Dezelfde pijl-omhoog-notatie werd door Ronald Graham gebruikt om enkele eigenschappen van een hyperkubus (een kubus in 4 ruimtelijke dimensies) te beperken, hoewel ‘Grahams getal’ nu beter bekend is omdat het gewoonweg kolossaal is.

Grahams getal is als volgt gedefinieerd:

Het aantal pijlen in elke laag wordt gegeven door het resultaat van de evaluatie van de pijlen in de laag eronder, totdat na 64 lagen het uiteindelijke aantal is bereikt. Om je een idee te geven van de grootte hiervan, kunnen we alleen naar de eerste laag kijken:

waar het aantal drieën in de uitdrukking rechts is

Nu reduceert elke tetrering () operatie tot een “toren” van exponentiaties () volgens de definitie

waar er X drieën zijn.

Dus,

waar het aantal drietallen, wordt, uitsluitend in termen van herhaalde “exponentiatietorens”, en waarbij het aantal drieën in elke toren, te beginnen bij de meest linkse toren, wordt bepaald door de waarde van de volgende toren rechts.

Dat is, technisch gesproken, een heleboel drieën. Ontspan u echter nog niet, want het getal van Graham is weliswaar het grootste getal dat wiskundigen tot nu toe expliciet hebben moeten opschrijven, maar wordt in de schaduw gesteld door sommige producten van de computertheorie. We hebben hier niet de ruimte om ze te bespreken, maar kijk eens naar ‘Who can write down the bigger number?’ van Scott Aaronson als Grahams getal net niet genoeg voor je was. Het gaat ook dieper in op de geschiedenis van grote getallen en hun verklaringen.

Groot, Groter, Grootst

De wereld van getallen is, zoals je zou verwachten, oneindig. De natuur is behoorlijk groot, maar de getallen die zij van ons verlangt zijn veel kleiner dan de getallen die menselijke wiskundigen hebben bedacht. In die zin is de menselijke geest groter dan het universum.