Wprowadzając wartości liczbowe w polach odpowiedzi, można używać liczb całkowitych (1000, 0x3E8, 0b1111101000), liczb zmiennoprzecinkowych (1000.0), notacji naukowej (1e3), współczynników skali inżynierskiej (1K) lub wyrażeń liczbowych (3*300 + 100).Przydatne linki:
- Wprowadzenie do Jade
- Biblioteka komórek standardowych
Problem 1. Problem projektowy: 32-bitowa jednostka arytmetyczno-logicznaZapoznaj się z poniższymi instrukcjami.Użyj poniższej instancji Jade, aby wprowadzić swój projekt. Aby zakończyć ten problem projektowy, wybierz moduł /alu/alu i kliknij na pasku narzędzi Jade, a wbudowany tester albo zgłosi wszelkie rozbieżności między oczekiwanymi i rzeczywistymi wyjściami, albo, jeśli Twój projekt jest poprawny, zapisze test zaliczony.{ „shared_modules”: , „hierarchical”: „true”, „parts”: , „tools”: , „editors”: , „edit”: „/alu/alu”, „required_tests”: } W tym laboratorium zbudujemy jednostkę arytmetyczno-logiczną (ALU) dla procesora Beta. ALU ma dwa 32-bitowe wejścia (które będziemy nazywać „A” i „B”) i wytwarza jedno 32-bitowe wyjście. Zaczniemy od zaprojektowania każdego fragmentu ALU jako osobnego układu, z których każdy wytwarza własne 32-bitowe wyjście. Następnie połączymy te wyjścia w jeden wynik ALU.Podczas projektowania obwodów istnieją trzy oddzielne czynniki, które można zoptymalizować:
- projektowanie dla maksymalnej wydajności (minimalne opóźnienie)
- projektowanie dla minimalnego kosztu (minimalny obszar)
- projektowanie dla najlepszego stosunku kosztu do wydajności (minimalizacja obszaru* opóźnienie)
Szczęśliwie często możliwe jest zrobienie wszystkich trzech rzeczy naraz, ale w niektórych częściach obwodu trzeba będzie dokonać pewnego rodzaju kompromisu. Podczas projektowania obwodów powinieneś wybrać, który z tych trzech czynników jest dla ciebie najważniejszy i odpowiednio zoptymalizować swój projekt. The standard cell library & gate-level simulationThe building blocks for this lab come from a library of logicgates – IC manufacturers often have a „standard cell library” andvarious design tools to make it easier for their customers to designwithstanding without worrying about the detailed geometry of the mask layers usedto create mosfets and wiring. 6.004 ma swoją własną bibliotekę komórek standardowych, która zawiera:
inwerter, bufory, sterownik trójstanowy
2-, 3- i 4-wejściowe bramki AND, OR, NAND i NOR
2-wejściowe bramki XOR i XNOR
2:1 i 4:1 multipleksery
D-register i D-latche
Szczegóły dotyczące odpowiednich połączeń dla każdej bramki można znaleźć w dokumentacji biblioteki. W Jade, bramki w standardowej bibliotece komórek można znaleźć w pojemniku z częściami pod „/gates/”.
Ponieważ projektujemy na poziomie bramek, możemy użyć fastersymulatora, który zna tylko bramki i wartości logiczne (zamiast tranzystorów i napięć). Zauważ, że twój projekt nie może zawierać żadnych tranzystorów, rezystorów, kondensatorów itp.; symulator na poziomie bramek obsługuje tylko prymitywy bramkowe ze standardowej biblioteki komórek.Wejścia są nadal określone w kategoriach napięć (aby zachować zgodność listy sieciowej z innymi symulatorami), ale symulator poziomu bramek konwertuje napięcia na jedną z trzech możliwych wartości logicznych, używając progów vil i vih określonych na początku twojego pliku projektowego:
0 logicznie niski (napięcia mniejsze lub równe progowi vil)
1 logicznie wysoki (napięcia większe lub równe progowi vih)
X nieznany lub nieokreślony (napięcia pomiędzy progami, lub nieznane napięcia)
Czwarta wartość „Z” jest używana do reprezentowania wartości węzłów, które nie są napędzane przez żadne wyjście bramki (np.g., wyjścia tristatedriverów, które nie są włączone). Poniższy diagram pokazuje, jak te wartości pojawiają się na wyświetlaczu przebiegu:
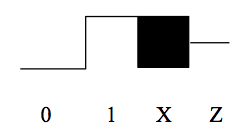
Specyfikacja ALU
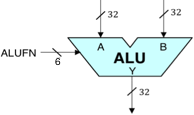
Zbudowany przez nas 32-bitowy ALU będzie elementem składowym Betaprocesora, którym zajmiemy się w kolejnych laboratoriach. Symbol logiczny dla naszego ALU jest pokazany po prawej stronie. Jest to układ kombinacyjny, który pobiera dwa 32-bitowe słowa danych A i B jako wejścia i wytwarza 32-bitowe wyjście Y poprzez wykonanie określonej funkcji arytmetycznej lub logicznej na wejściach A i B. Konkretna funkcja, która ma być wykonana, jest określona przez 6-bitowe wejście sterujące FN, którego wartość koduje funkcję zgodnie z poniższą tabelą:
| FN |
Operacja |
Wartość wyjściowa Y |
| 00-011 |
CMPEQ |
Y = (A == B) |
| |
00-101 |
CMPLT |
Y = (A < B) |
| 00-111 |
CMPLE |
Y = (A ≤ B) |
| 01—0 |
32-bit ADD |
Y = A + B |
| 01-.–1 |
32-bit SUBTRACT |
Y = A – B |
| 10abcd |
Bit-wise Boolean |
Y = Fabcd(A,B) |
| 11–00 |
Logical Shift left (SHL) |
Y = A << B |
| 11-.-01 |
Logical Shift right (SHR) |
Y = A >> B |
| 11-.-11 |
Arithmetic Shift right (SRA) |
Y = A >> B (sign extended) |
Zauważ, że poprzez określenie odpowiedniej wartości dla 6-bitowego wejścia FNinput, ALU może wykonywać różne operacje arytmetyczne, porównania, przesunięcia i bitowe kombinacje Boolean wymagane przez nasz procesor Beta.
| Bi |
Ai |
Yi |
| 0 |
0 |
d |
| 0 |
1 |
c |
.
| 1 |
0 |
b |
| 1 |
1 |
a |
Bitowe operacje boolowskie są określone przez FN=10; w tym przypadku, pozostałe bity FN abcd są brane jako pozycje w tabeli prawdy opisującej, jak każdy bit Y jest określany przez odpowiadające mu bity A i B, jak pokazano po prawej stronie.Każda z trzech operacji porównania daje wyjście typu Boolean. W tych przypadkach Y są wszystkie zerowe, a bit niskiego rzędu Y jest 0 lub 1, odzwierciedlając wynik porównania 32-bitowych operandów A i B. Możemy podejść do projektu ALU dzieląc go na podsystemy poświęcone operacjom arytmetycznym, porównania, Boolean i przesunięcia, jak pokazano poniżej:
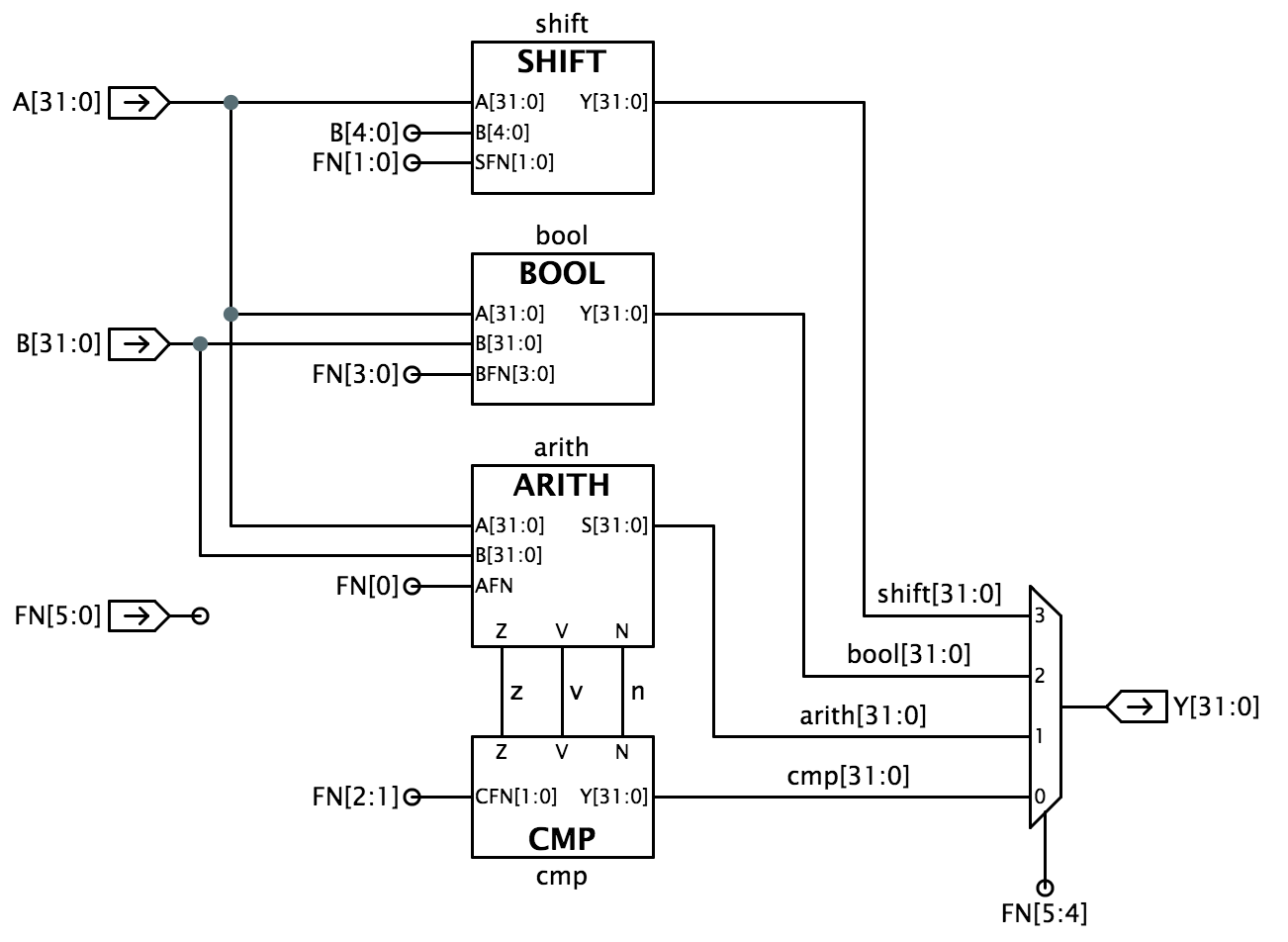
Projektowanie tak złożonego systemu jak ALU najlepiej wykonywać etapami, pozwalając na projektowanie i debugowanie poszczególnych podsystemów po kolei. Poniższe kroki podążają za tym podejściem do implementacji schematu ALUblock pokazanego powyżej. Zaczynamy od zaimplementowania struktury ALU z atrapami modułów dla każdego z czterech głównych podsystemów (BOOL, ARITH, CMP i SHIFT); następnie implementujemy i debugujemy rzeczywiste wersje każdego podsystemu. Aby ułatwić Ci podążanie tą ścieżką, zamieszczamy osobne testy dla każdego z czterech modułów składowych.UWAGA: sygnały FN używane do sterowania działaniem obwodu ALU używają kodowania wybranego w celu uproszczenia projektu obwodu ALU. To kodowanie nie jest takie samo jak kodowanie 6-bitowego pola opcode instrukcji Beta. W laboratorium 5 zbudujesz układ logiczny (właściwie ROM), który będzie tłumaczył pole opcode instrukcji na odpowiednie bity sterujące FN. Poniżej znajdują się uwagi projektowe sugerujące, jak zaprojektować każdy z podmodułów. Jednostka BOOL Zaprojektuj układ do implementacji operacji Boolean dla twojego ALU i użyj go do zastąpienia zworki i przewodu, który łączy wyjście Youtput z masą.
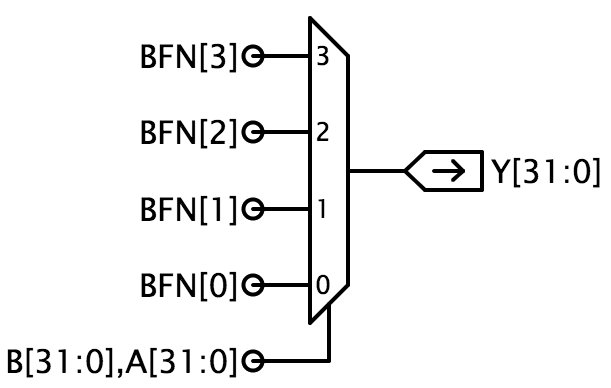
Sugerowana implementacja używa 32 kopii multipleksera 4 do 1 (mux4), gdzie BFN kodują operację, która ma być wykonana, a A i B są podłączone do wejść selectinput multipleksera. Ta implementacja może produkować dowolną z 16 dwuwejściowych funkcji boole’owskich.
Podpowiedź: Jade automatycznie replikuje bramkę logiczną, aby dopasować szerokość jej wejść i wyjść do szerokości sygnałów, które łączą się z bramką. Na przykład, bramka MUX4 pokazana powyżej ma 1-bitowy sygnał wyjściowy, który w tym schemacie jest podłączony do Y, sygnału o szerokości 32. Tak więc Jade będzie replikował MUX4 32 razy, wyjście pierwszego MUX4 łączy się z Y, wyjście drugiego MUX4 łączy się z Y, i tak dalej. Sygnały wejściowe są następnie replikowane (jeśli to konieczne), aby zapewnić wejścia dla każdej z 32 bramek MUX4. Każda bramka MUX4 wymaga 2 sygnałów selekcji, które są pobierane z 64 dostarczonych sygnałów. B i A łączą się z liniami selekcyjnymi pierwszego MUX4, B i A łączą się z liniami selekcyjnymi drugiego MUX4, i tak dalej. Każda bramka MUX4 wymaga 4 sygnałów danych. Określone wejścia BFN mają szerokość tylko 1 bitu, więc określone sygnały są powielane 32 razy, np. BFN jest używany jako wejście D0 dla każdego z 32 MUX4.
Poniższa tabela pokazuje kodowanie niektórych sygnałów sterujących BFN używanych przez testowy dżig (i w naszych typowych Betaimplementacjach):
| Operacja |
BFN |
| AND |
1000 |
| OR |
1110 |
| XOR |
0110 |
| „A” |
1010 |
Test BOOL faktycznie sprawdza wszystkie 16 operacji boolean na aselekcji argumentów, i zgłosi wszelkie błędy, które znajdzie.Kiedy twój układ BOOL został wprowadzony, uruchom test klikając na zielony znacznik; powinno pojawić się okno symulacji pokazujące wejścia i wyjścia. Jade sprawdzi wyniki twojego obwodu z listą oczekiwanych wartości i zgłosi wszelkie rozbieżności, jakie znajdzie.
Podpowiedź: Co zrobić, gdy weryfikacja nie powiedzie się? Powiadomienie o niepowodzeniu powie Ci, który sygnał nie przeszedł weryfikacji i symulowany czas, w którym wystąpiło niedopasowanie między wartością rzeczywistą a oczekiwaną. Testy są w rzeczywistości sekwencją 100ns cykli testowych, a raportowany czas będzie na końcu jednego z cykli, kiedy wartości wyjściowe są sprawdzane pod kątem poprawności. Przesuwać mysz nad wykresem odpowiedniego przebiegu sygnału, aż pionowy kursor czasu znajdzie się w przybliżeniu w czasie awarii. Następnie kliknij dwukrotnie, aby powiększyć wykresy wokół tego konkretnego czasu; powiększyć na tyle, aby wszystkie sygnały dla tego cyklu testowego były czytelne. Teraz możesz dowiedzieć się, co obwód miał zrobić w tym konkretnym teście i, miejmy nadzieję, wywnioskować, dlaczego twój obwód wytwarza nieprawidłowe wyjście.
Jednostka ARITHZaprojektuj jednostkę dodawania/podejmowania (ARITH), która operuje na 32-bitowych wejściach uzupełniających i generuje 32-bitowe wyjście. Przydatne będzie wygenerowanie trzech innych sygnałów wyjściowych, które będą używane przez jednostkę CMP: Z, który jest prawdziwy, gdy wszystkie wyjścia S są zerowe, V, który jest prawdziwy, gdy operacja dodawania przepełnia się (tzn. wynik jest zbyt duży, aby można go było przedstawić w 32 bitach), oraz N, który jest prawdziwy, gdy suma jest ujemna (tzn, S = 1).Przepełnienie nigdy nie może wystąpić, gdy dwa operandy dodawania mają różne znaki; jeśli dwa operandy mają ten sam znak, to przepełnienie można wykryć, jeśli znak wyniku różni się od znaku operandów:
\(V = XA_{31} \\\) XB_{31} \overline{S_{31} + \overline{XA_{31}}overline{XB_{31}} S_{31}})Zauważ, że to równanie używa XB, który jest bitem wysokiego rzędu operandu B do samego addera (tj. po bramce XOR – patrz schemat poniżej). XA to po prostu A. Poniższy schemat jest jedną z sugestii, jak zabrać się za projektowanie:

AFN będzie ustawiony na 0 dla ADD (\(S = A+B\)) i 1 dla SUBTRACT (\(S = A-B\)); A i B są 32-bitowymi operandami wejściowymi z uzupełnieniem dwójkowym; S jest 32-bitowym wynikiem; Z/V/N są trzema kodami warunkowymi opisanymi powyżej. Będziemy stosować konwencję numeracji bitów „little-endian”, gdzie bit 31 jest bitem o największym znaczeniu, a bit 0 jest bitem o najmniejszym znaczeniu.Dostarczyliśmy moduł FA do wprowadzania schematu na poziomie bramek dla pełnego sumatora (zobacz Problem 8 z Laboratorium #1), który ma być użyty do skonstruowania 32-bitowego sumatora ripple carry, stanowiącego serce jednostki ARITH. Sygnał wejściowy AFN wybiera, czy operacja ma być ADD czy SUBTRACT. Aby wykonać SUBTRACT, układ najpierw oblicza negację dopełnienia do dwóch operandów B przez odwrócenie B, a następnie dodaje jeden (można to zrobić przez wymuszenie, aby carry-in 32-bitowego dodawania wynosiło 1). Zacznij od zaimplementowania 32-bitowego dodawania używając architektury aripple-carry (będziesz mógł to poprawić w dalszej części kursu). Będziesz musiał skonstruować 32-wejściową bramkę NOR potrzebną do obliczenia Z, używając drzewa mniejszych bramek typu fan-in (w bibliotece części dostępne są tylko bramki z maksymalnie 4 wejściami). Podczas wprowadzania obwodów pamiętaj o usunięciu oryginalnych zworników i przewodów, które łączyły wyjścia z masą! Test modułu próbuje dodawać i odejmować różne operandy, upewniając się, że wyjścia Z, V i N są poprawne po każdej operacji. Jednostka CMPU zapewnia trzy operacje porównania dla operandów A i B. Możemy użyć jednostki dodawania zaprojektowanej powyżej, aby obliczyć A-B, a następnie spojrzeć na wynik (właściwie tylko kody warunków Z, V i N), aby określić, czy A=B, A < B lub A ≤ B. Operacje porównania generują 32-bitowy wynik, używając liczby 0 jako reprezentującej fałsz i liczby 1 jako reprezentującej prawdę.Zaprojektować 32-bitową jednostkę porównującą (CMP), która generuje jedną z dwóch stałych (0 lub 1) w zależności od sygnałów sterujących CFN (używanych do wyboru porównania, które ma być wykonane) oraz wyjść Z, V i N jednostki dodającej/odejmującej. Oczywiście 31 bitów wysokiego rzędu na wyjściu jest zawsze zerowe. Najmniej znaczący bit (LSB) wyjścia jest określany przez wykonywane porównanie i wyniki odejmowania przeprowadzonego przez sumator/podtraktor:
| Porównanie |
Equation for LSB |
CFN |
| A = B |
LSB = \(Z\) |
01 |
| A < B |
LSB = \(N \\ V \) |
10 |
| A ≤ B |
LSB = \(Z + (N \oplus V) |
11 |
Na poziomie modułu ALU, FN są używane do sterowania jednostką porównującą, ponieważ musimy użyć FN do sterowania jednostką dodającą/podejmującą, aby wymusić odejmowanie.Uwaga dotycząca wydajności: wejścia Z, V i N do tego układu mogą być obliczone przez jednostkę dodającą/podtrajającą dopiero po zakończeniu 32-bitowego dodawania. Oznacza to, że pojawiają się one dość późno i wymagają dalszego przetwarzania w tym module, co z kolei sprawia, że Y pojawia się bardzo późno w grze. Możesz to znacznie przyspieszyć, myśląc o względnym czasie Z, V i N, a następnie projektując swoją logikę tak, aby zminimalizować ścieżki opóźnień z udziałem późno docierających sygnałów.Test modułu zapewnia, że poprawna odpowiedź jest generowana dla wszystkich możliwych kombinacji Z, V, N i CFN. Jednostka SHIFTZaprojektuj 32-bitowy przerzutnik, który realizuje operacje logicznego przesunięcia w lewo (SHL), logicznego przesunięcia w prawo (SHR) oraz arytmetycznego przesunięcia w prawo (SRA). Operand A dostarcza dane, które mają być przesunięte, a 5 bitów niskiego rzędu operandu B jest używane jako licznik przesunięcia (tzn. od 0 do 31 bitów przesunięcia). Żądana operacja zostanie zakodowana w SFN w następujący sposób:
| Operacja |
SFN |
| SHL (shift left) |
00 |
| SHR (shift right) |
01 |
| SRA (shift right with sign extension ) |
11 |
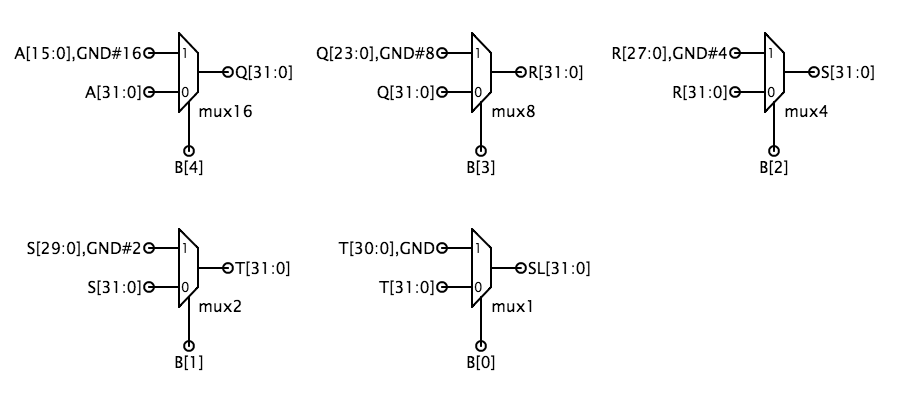
Z tym kodowaniem, SFN wynosi 0 dla przesunięcia w lewo i 1 dla przesunięcia w prawo, a SFN kontroluje logikę rozszerzenia znaku przy przesunięciu w prawo. Dla SHL i SHR, 0 są przesuwane na zwolnione pozycje bitowe. Dla SRA („shift right arithmetic”), wszystkie wolne pozycje bitowe są wypełniane A, bitem znaku oryginalnych danych, tak że wynik będzie taki sam jak podział oryginalnych danych przez odpowiednią potęgę 2. Najprostszą implementacją jest zbudowanie dwóch przerzutników – jednego dla przesunięcia w lewo i jednego dla przesunięcia w prawo – a następnie użycie dwukierunkowego 32-bitowego multipleksera do wybrania odpowiedniej odpowiedzi jako wyjścia modułu. Łatwo jest zbudować przerzutnik, gdy zauważymy, że wielobitowe przesunięcie może być zrealizowane przez kaskadowe przesunięcia o różne potęgi 2. Na przykład, 13-bitowe przesunięcie może być zrealizowane przez przesunięcie o 8, a następnie o 4, a następnie o 1. Przerzutnik jest po prostu kaskadą multiplekserów, z których każdy jest sterowany przez jeden bit liczby przesunięć. Poniższy schemat pokazuje możliwą implementację logiki przesunięcia w lewo; logika przesunięcia w prawo jest podobna z niewielką dodatkową komplikacją polegającą na konieczności przesunięcia albo 0 (tj. „gnd”) albo A, w zależności od wartościSFN. Innym podejściem, które oszczędza bramki, jest użycie logiki leftshift zarówno dla lewych, jak i prawych przesunięć, ale dla przesunięć w prawo, odwrócenie bitów operandu A na drodze wejścia i odwrócenie bitów wyjścia na drodze wyjścia.
Test modułu sprawdza, czy wszystkie trzy typy przesunięć działają poprawnie. Testy końcowePo zaprojektowaniu czterech podmodułów należy wybrać moduł ALU i uruchomić jego test. To uruchamia każdy z zestawów testów, których użyłeś do debugowania podukładów składowych, więc jeśli nie ma jakiejś nieprzewidzianej interakcji między blokami, prawdopodobnie przejdziesz ten test. Kiedy ten test zakończy się sukcesem, system oznaczy Twój projekt jako kompletny. Zadanie 2. Testowanie ALUW zadaniu projektowym tego laboratorium (patrz wyżej) zbudujesz 32-bitową jednostkę arytmetyczno-logiczną (ALU), która wykonuje operacje arytmetyczno-logiczne na 32-bitowych operandach, dając 32-bitowy wynik. Możesz najpierw popracować nad problemem projektowym, a potem wrócić do tego zadania. Test do tego laboratorium weryfikuje Twój układ ALU przez zastosowanie 186 różnych zestawów wartości wejściowych. To pytanie bada, jak te wartości zostały wybrane.Żaden projektant, którego znam, nie uważa, że testowanie jest zabawne – projektowanie obwodu wydaje się o wiele bardziej interesujące niż upewnianie się, że działa.Ale błędny projekt też nie jest zbyt zabawny! Pamiętaj, że dobry inżynier nie tylko wie, jak budować dobre projekty, ale także faktycznie buduje dobre projekty, a to oznacza testowanie projektu, aby upewnić się, że robi to, co mówisz, że robi.Oczywistym sposobem testowania obwodu kombinacyjnego jest wypróbowanie wszystkich możliwych kombinacji wejść, sprawdzając prawidłowe wartości wyjściowe po zastosowaniu każdej kombinacji wejść. Ten rodzaj testu wyczerpującego dowodzi poprawności działania poprzez wyliczenie tabeli prawdy urządzenia kombinacyjnego. Jest to skuteczna strategia dla układów z kilkoma wejściami, ale szybko staje się niepraktyczna dla układów z wieloma wejściami. Wykorzystując informacje o tym, jak obwód jest skonstruowany, możemy znacznie zredukować liczbę kombinacji wejść potrzebnych do przetestowania obwodu.Architektura sumatora ripple-carry zaproponowana w Zadaniu Projektowym wykorzystuje 32 kopie modułu pełnego sumatora do stworzenia 32-bitowego sumatora.Każdy pełny sumator ma 3 wejścia (A, B, CI) i dwa wyjścia (S, CO):
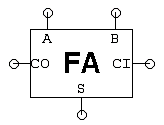
- Pojedynczy wektor testowy dla pełnego addera składa się z 3 wartości wejściowych (po jednej dla A, B i CI) oraz 2 wartości wyjściowych (S i CO). Aby przeprowadzić test, wartości wejściowe z bieżącego wektora testowego są stosowane do testowanego urządzenia, a następnie rzeczywiste wartości wyjściowe są porównywane z oczekiwanymi wartościami wymienionymi przez wektor testowy. Proces ten jest powtarzany aż do wykorzystania wszystkich wektorów testowych. Zakładając, że nie wiemy nic o wewnętrznych układach sumatora, ile wektorów testowych potrzebowalibyśmy, aby wyczerpująco przetestować jego funkcjonalność? Liczba wektorów testowych do wyczerpującego przetestowania pełnego addera?
- Rozważmy 32-bitowy sumator z 64 wejściami (dwa 32-bitowe operandy wejściowe, załóżmy, że CIN jest związany z masą, jak pokazano na poniższym schemacie) i 32 wyjściami (32-bitowy wynik). Załóżmy, że nie wiemy nic o jego wewnętrznym układzie i nie możemy wykluczyć, że dla dowolnej kombinacji wejść może on otrzymać błędną odpowiedź. Innymi słowy, to, że dodawarka otrzymała poprawną odpowiedź dla 2 + 3, nie pozwala nam wyciągnąć żadnych wniosków na temat tego, jaką odpowiedź otrzymałaby dla 2 + 7. Gdybyśmy mogli stosować jeden wektor testowy co 100ns, ile czasu zajęłoby nam wyczerpujące przetestowanie addera? Czas na wyczerpujące przetestowanie 32-bitowego addera? (w latach)
- Wyraźnie widać, że testowanie 32-bitowego sumatora poprzez próbowanie wszystkich kombinacji wartości wejściowych nie jest dobrym planem! Poniżej pokazany jest schemat 32-bitowego addera ripple-carry.
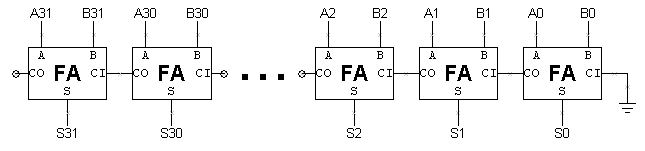 Z wyjątkiem przeniesienia z bitu po prawej stronie, każdy bit sumatora działa niezależnie. Możemy wykorzystać tę obserwację do testowania addera bit po bicie i przy odrobinie pomyślunku możemy faktycznie przeprowadzić wiele z tych testów równolegle. W tym przypadku fakt, że dodawarka otrzymała poprawną odpowiedź dla 2 + 3, mówi nam wiele o odpowiedzi, jaką otrzyma dla 2 + 7. Ponieważ obliczenia wykonywane przez bity addera 0 i 1 są takie same w obu przypadkach, jeśli odpowiedź dla 2 + 3 jest poprawna, dwa bity niskiego rzędu odpowiedzi dla 2 + 7 będą również poprawne. Tak więc nasz plan testowania ripple-carry adder polega na testowaniu każdego pełnego addera niezależnie. Podczas testowania bitu N możemy ustawić A i B bezpośrednio z wektora testowego. Ustawienie CI na konkretną wartość wymaga nieco więcej pracy, ale możemy to zrobić, jeśli odpowiednio dobierzemy A i B. Jeśli chcemy ustawić CI na 0, to jakie wartości powinny mieć A i B? Jeśli chcemy ustawić CI na 1? Przyjmij, że nie możemy nic zakładać na temat wartości CI. Wartości A i B, aby C=0? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Wartości A i B, aby C=1? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Dzięki tej strategii możemy testować parzyste bity sumatora równolegle z jednym zestawem wektorów testowych i testować nieparzyste bity sumatora równolegle z innym zestawem wektorów testowych. Oto zestaw 10 wektorów testowych, które powinny przetestować wszystkie kombinacje wartości wejściowych dla każdego FA w 32-bitowym adderze ripple-carry:
Z wyjątkiem przeniesienia z bitu po prawej stronie, każdy bit sumatora działa niezależnie. Możemy wykorzystać tę obserwację do testowania addera bit po bicie i przy odrobinie pomyślunku możemy faktycznie przeprowadzić wiele z tych testów równolegle. W tym przypadku fakt, że dodawarka otrzymała poprawną odpowiedź dla 2 + 3, mówi nam wiele o odpowiedzi, jaką otrzyma dla 2 + 7. Ponieważ obliczenia wykonywane przez bity addera 0 i 1 są takie same w obu przypadkach, jeśli odpowiedź dla 2 + 3 jest poprawna, dwa bity niskiego rzędu odpowiedzi dla 2 + 7 będą również poprawne. Tak więc nasz plan testowania ripple-carry adder polega na testowaniu każdego pełnego addera niezależnie. Podczas testowania bitu N możemy ustawić A i B bezpośrednio z wektora testowego. Ustawienie CI na konkretną wartość wymaga nieco więcej pracy, ale możemy to zrobić, jeśli odpowiednio dobierzemy A i B. Jeśli chcemy ustawić CI na 0, to jakie wartości powinny mieć A i B? Jeśli chcemy ustawić CI na 1? Przyjmij, że nie możemy nic zakładać na temat wartości CI. Wartości A i B, aby C=0? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Wartości A i B, aby C=1? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Dzięki tej strategii możemy testować parzyste bity sumatora równolegle z jednym zestawem wektorów testowych i testować nieparzyste bity sumatora równolegle z innym zestawem wektorów testowych. Oto zestaw 10 wektorów testowych, które powinny przetestować wszystkie kombinacje wartości wejściowych dla każdego FA w 32-bitowym adderze ripple-carry:
| bity 0, 2, … |
bity 1, 3, … |
A |
B |
| A=0, B=0, CI=0 |
A=0, B=0, CI=0 |
0x000000 |
0x000000 |
| A=1, B=0, CI=0 |
A=0, B=0, CI=0 |
0x55555555 |
0x000000 |
| A=0, B=1, CI=0 |
A=0, B=0, CI=0 |
0x000000 |
0x555555 |
| A=1, B=1, CI=0 |
A=0, B=0, CI=1 |
0x555555 |
0x55555555 |
| A=0, B=0, CI=0 |
A=1, B=0, CI=0 |
0xAAAAAAAA |
0x000000 |
| A=0, B=0, CI=0 |
A=0, B=1, CI=0 |
0x000000 |
0xAAAAAA |
| A=0, B=0, CI=1 |
A=1, B=1, CI=0 |
0xAAAAAA |
0xAAAAAA |
| A=1, B=0, CI=1 |
A=1, B=0, CI=1 |
0xFFFFFFFF |
0x00000001 |
| A=0, B=1, CI=1 |
A=0, B=1, CI=1 |
0x00000001 |
0xFFFFFFFF |
| A=1, B=1, CI=1 |
A=1, B=1, CI=1 |
0xFFFFFFFF |
0xFFFFFFFF |
- Trzy z wejść jednostki porównującej (Z, V i N) pochodzą z addera/podtraktora pracującego w trybie odejmowania obliczającego A-B:
Z = 1, jeśli A-B jest równe 0 N = 1, jeśli A-B jest ujemne (OUT = 1) V = 1, jeśli nastąpiło przepełnienie. ALU, które posiada tylko adder, oblicza A-B jako A+(-B) = A+(~B)+1. Niech XB = ~B, bitowe dopełnienie B. Przepełnienie występuje, jeśli znak wyniku (OUT) różni się od znaków operandów addera (A, XB). Zauważ, że jeśli znaki A i XB są różne, to dodawanie nie może spowodować przepełnienia.Aby przetestować jednostkę porównującą, musimy wybrać operandy dla dodawarki/odejmującej, które generują wszystkie możliwe kombinacje Z, V i N. Łatwo zauważyć, że każda kombinacja z Z = 1 i N = 1 nie jest możliwa (wyjście dodawarki nie może być jednocześnie ujemne i zerowe!). Okazuje się również, że kombinacje z Z = 1 i V =1 nie mogą być wytworzone przez operację odejmowania. Dla każdej z kombinacji Z, V i N pokazanych poniżej, wybierz operację odejmowania, która wytworzy określoną kombinację kodów stanu. Odejmowanie, które daje Z=0, V=0, N=0? 0x12345678 – 0x12345678 0x7FFFFFFF – 0xFFFFFFFF 0x00000005 – 0xDEADBEEF 0xDEADBEEF – 0x00000005 0x80000000 – 0x00000001 Odejmowanie, które daje Z=1, V=0, N=0? 0x12345678 – 0x12345678 0x7FFFFFFF – 0xFFFFFFFF 0x00000005 – 0xDEADBEEF 0xDEADBEEF – 0x00000005 0x80000000 – 0x00000001 Odejmowanie, które daje Z=0, V=1, N=0? 0x12345678 – 0x12345678 0x7FFFFFFF – 0xFFFFFFFF 0x00000005 – 0xDEADBEEF 0xDEADBEEF – 0x00000005 0x80000000 – 0x00000001 Odejmowanie, które daje Z=0, V=0, N=1? 0x12345678 – 0x12345678 0x7FFFFFFF – 0xFFFFFFFF 0x00000005 – 0xDEADBEEF 0xDEADBEEF – 0x00000005 0x80000000 – 0x00000001 Odejmowanie, które daje Z=0, V=1, N=1? 0x12345678 – 0x12345678 0x7FFFFFFF – 0xFFFFFFFFFF 0x00000005 – 0xDEADBEEF 0xDEADBEEF – 0x00000005 0x80000000 – 0x00000001 Problem 3. Wszechstronna jednostka BOOL
| Bi |
Ai |
Yi |
| 0 |
0 |
d |
| 0 |
.
1 |
c |
| 1 |
0 |
b |
| 1 |
1 |
a |
Jak widzieliśmy w instrukcjach dla ALU,bitowe operacje Boolean są określone przez FN=10. W tym przypadku, pozostałe bity FN abcd są brane jako wpisy w tabeli prawdy opisującej jak każdy bit Y jest określany przez odpowiadające mu bity A i B, jak pokazano po prawej stronie. Dla każdej z operacji boole’owskich (F(A,B)\) określonych poniżej, określ ustawienia dla FN tak, aby jednostka Bool obliczyła żądaną operację. AND(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 OR(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 XOR(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 NAND(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 NOR(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 XNOR(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 A: FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 B: FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

 Zbudowany przez nas 32-bitowy ALU będzie elementem składowym Betaprocesora, którym zajmiemy się w kolejnych laboratoriach. Symbol logiczny dla naszego ALU jest pokazany po prawej stronie. Jest to układ kombinacyjny, który pobiera dwa 32-bitowe słowa danych A i B jako wejścia i wytwarza 32-bitowe wyjście Y poprzez wykonanie określonej funkcji arytmetycznej lub logicznej na wejściach A i B. Konkretna funkcja, która ma być wykonana, jest określona przez 6-bitowe wejście sterujące FN, którego wartość koduje funkcję zgodnie z poniższą tabelą:
Zbudowany przez nas 32-bitowy ALU będzie elementem składowym Betaprocesora, którym zajmiemy się w kolejnych laboratoriach. Symbol logiczny dla naszego ALU jest pokazany po prawej stronie. Jest to układ kombinacyjny, który pobiera dwa 32-bitowe słowa danych A i B jako wejścia i wytwarza 32-bitowe wyjście Y poprzez wykonanie określonej funkcji arytmetycznej lub logicznej na wejściach A i B. Konkretna funkcja, która ma być wykonana, jest określona przez 6-bitowe wejście sterujące FN, którego wartość koduje funkcję zgodnie z poniższą tabelą:

 Sugerowana implementacja używa 32 kopii multipleksera 4 do 1 (mux4), gdzie BFN kodują operację, która ma być wykonana, a A i B są podłączone do wejść selectinput multipleksera. Ta implementacja może produkować dowolną z 16 dwuwejściowych funkcji boole’owskich.
Sugerowana implementacja używa 32 kopii multipleksera 4 do 1 (mux4), gdzie BFN kodują operację, która ma być wykonana, a A i B są podłączone do wejść selectinput multipleksera. Ta implementacja może produkować dowolną z 16 dwuwejściowych funkcji boole’owskich.



 Z wyjątkiem przeniesienia z bitu po prawej stronie, każdy bit sumatora działa niezależnie. Możemy wykorzystać tę obserwację do testowania addera bit po bicie i przy odrobinie pomyślunku możemy faktycznie przeprowadzić wiele z tych testów równolegle. W tym przypadku fakt, że dodawarka otrzymała poprawną odpowiedź dla 2 + 3, mówi nam wiele o odpowiedzi, jaką otrzyma dla 2 + 7. Ponieważ obliczenia wykonywane przez bity addera 0 i 1 są takie same w obu przypadkach, jeśli odpowiedź dla 2 + 3 jest poprawna, dwa bity niskiego rzędu odpowiedzi dla 2 + 7 będą również poprawne. Tak więc nasz plan testowania ripple-carry adder polega na testowaniu każdego pełnego addera niezależnie. Podczas testowania bitu N możemy ustawić A i B bezpośrednio z wektora testowego. Ustawienie CI na konkretną wartość wymaga nieco więcej pracy, ale możemy to zrobić, jeśli odpowiednio dobierzemy A i B. Jeśli chcemy ustawić CI na 0, to jakie wartości powinny mieć A i B? Jeśli chcemy ustawić CI na 1? Przyjmij, że nie możemy nic zakładać na temat wartości CI. Wartości A i B, aby C=0? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Wartości A i B, aby C=1? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Dzięki tej strategii możemy testować parzyste bity sumatora równolegle z jednym zestawem wektorów testowych i testować nieparzyste bity sumatora równolegle z innym zestawem wektorów testowych. Oto zestaw 10 wektorów testowych, które powinny przetestować wszystkie kombinacje wartości wejściowych dla każdego FA w 32-bitowym adderze ripple-carry:
Z wyjątkiem przeniesienia z bitu po prawej stronie, każdy bit sumatora działa niezależnie. Możemy wykorzystać tę obserwację do testowania addera bit po bicie i przy odrobinie pomyślunku możemy faktycznie przeprowadzić wiele z tych testów równolegle. W tym przypadku fakt, że dodawarka otrzymała poprawną odpowiedź dla 2 + 3, mówi nam wiele o odpowiedzi, jaką otrzyma dla 2 + 7. Ponieważ obliczenia wykonywane przez bity addera 0 i 1 są takie same w obu przypadkach, jeśli odpowiedź dla 2 + 3 jest poprawna, dwa bity niskiego rzędu odpowiedzi dla 2 + 7 będą również poprawne. Tak więc nasz plan testowania ripple-carry adder polega na testowaniu każdego pełnego addera niezależnie. Podczas testowania bitu N możemy ustawić A i B bezpośrednio z wektora testowego. Ustawienie CI na konkretną wartość wymaga nieco więcej pracy, ale możemy to zrobić, jeśli odpowiednio dobierzemy A i B. Jeśli chcemy ustawić CI na 0, to jakie wartości powinny mieć A i B? Jeśli chcemy ustawić CI na 1? Przyjmij, że nie możemy nic zakładać na temat wartości CI. Wartości A i B, aby C=0? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Wartości A i B, aby C=1? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Dzięki tej strategii możemy testować parzyste bity sumatora równolegle z jednym zestawem wektorów testowych i testować nieparzyste bity sumatora równolegle z innym zestawem wektorów testowych. Oto zestaw 10 wektorów testowych, które powinny przetestować wszystkie kombinacje wartości wejściowych dla każdego FA w 32-bitowym adderze ripple-carry: