Backpropagation Krok po kroku

Jeśli budujesz własną sieć neuronową, na pewno będziesz musiał zrozumieć jak ją trenować.Backpropagation jest powszechnie używaną techniką do trenowania sieci neuronowych. Istnieje wiele zasobów wyjaśniających tę technikę, ale ten post wyjaśni backpropagation z konkretnym przykładem w bardzo szczegółowych kolorowych krokach.

Możesz zobaczyć wizualizację przejścia do przodu i backpropagation tutaj. Możesz zbudować swoją sieć neuronową za pomocą netflow.js

Overview

W tym poście zbudujemy sieć neuronową z trzema warstwami:

• Warstwa wejściowa z dwoma neuronami wejściowymi
• Jedna warstwa ukryta z dwoma neuronami
• Warstwa wyjściowa z jednym neuronem

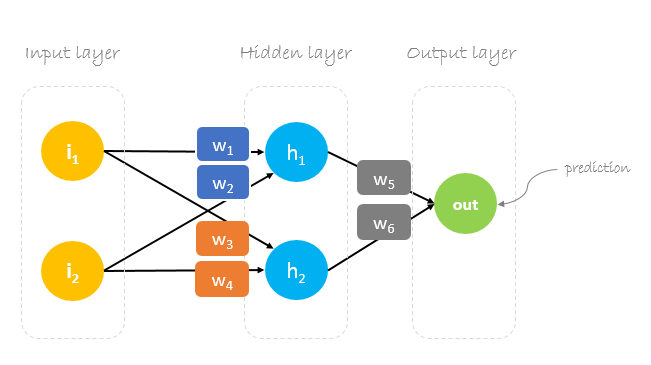
Wagi, wagi, wagi

Trenowanie sieci neuronowej polega na znalezieniu wag, które minimalizują błąd predykcji. Zazwyczaj rozpoczynamy trening z zestawem losowo wygenerowanych wag, a następnie za pomocą wstecznej propagacji aktualizujemy wagi, próbując poprawnie odwzorować dowolne dane wejściowe na dane wyjściowe.

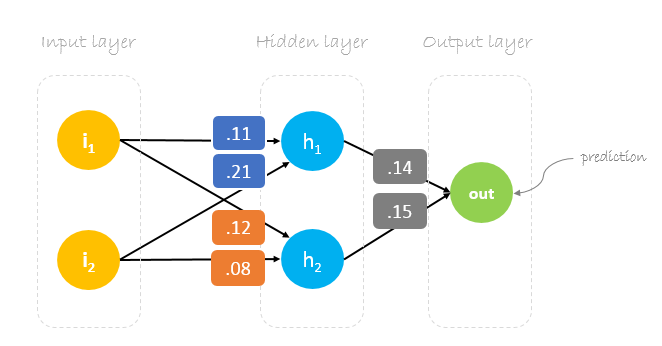
Nasze początkowe wagi będą wyglądały następująco:w1 = 0.11w2 = 0.21w3 = 0.12w4 = 0.08w5 = 0.14 i w6 = 0.15

Dataset

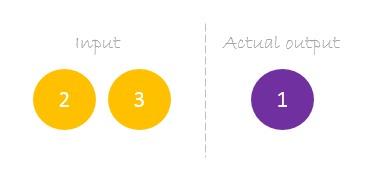
Nasz zbiór danych ma jedną próbkę z dwoma wejściami i jednym wyjściem.

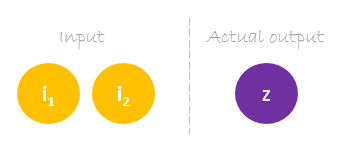
Nasza pojedyncza próbka jest następująca inputs= i output=.

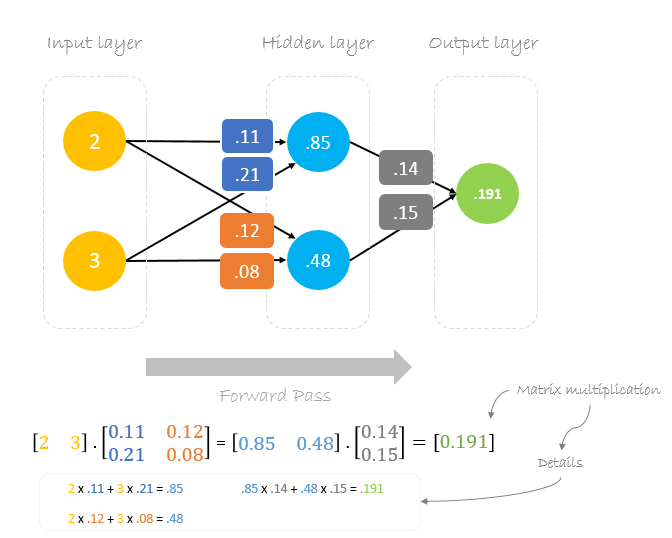
Forward Pass

Użyjemy podanych wag i danych wejściowych do przewidywania danych wyjściowych. Dane wejściowe są mnożone przez wagi, a wyniki są przekazywane do następnej warstwy.

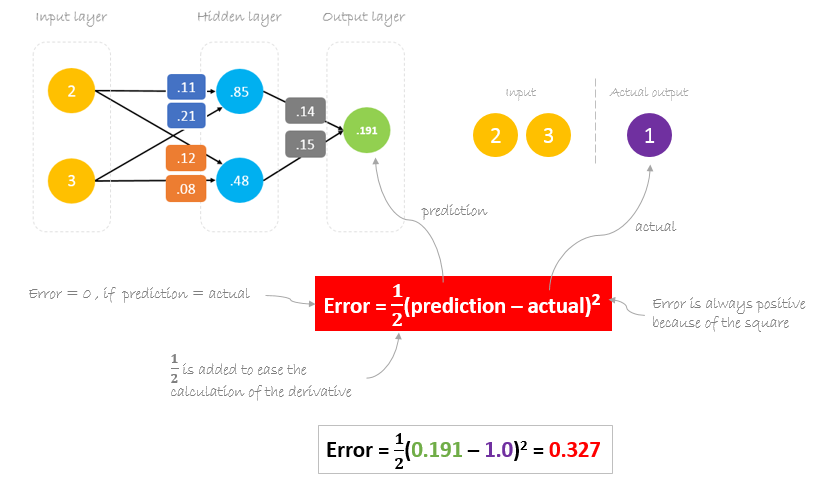
Obliczanie błędu

Teraz czas sprawdzić, jak nasza sieć sobie radzi, obliczając różnicę między rzeczywistym wyjściem a przewidywanym. Jest jasne, że nasze wyjście sieciowe, lub przewidywanie, nie jest nawet zbliżone do rzeczywistego. Możemy obliczyć różnicę lub błąd w następujący sposób.

Zmniejszanie błędu

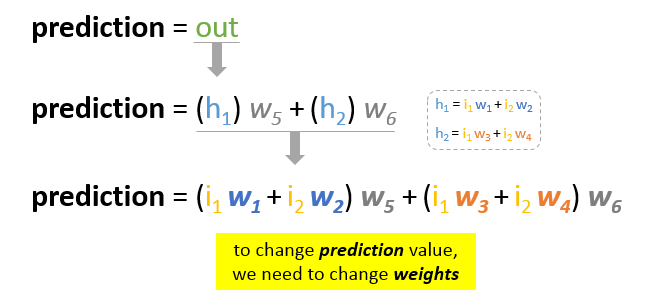
Naszym głównym celem treningu jest zmniejszenie błędu lub różnicy między przewidywaniem a rzeczywistym wyjściem. Ponieważ rzeczywista wartość wyjściowa jest stała, „nie zmienia się”, jedynym sposobem na zmniejszenie błędu jest zmiana wartości predykcji. Pytanie brzmi, jak zmienić wartość predykcji?

Rozkładając predykcję na jej podstawowe elementy, możemy stwierdzić, że zmiennymi wpływającymi na wartość predykcji są wagi. Innymi słowy, aby zmienić wartość predykcji, musimy zmienić wartości wag.

Pytanie brzmi teraz, jak zmienić wartość wag, aby zmniejszyć błąd?dpowiedź brzmi: Backpropagation!

Backpropagation

Backpropagation, skrót od „backward propagation of errors”, to mechanizm służący do aktualizacji wag za pomocą zejścia gradientowego. Oblicza gradient funkcji błędu w odniesieniu do wag sieci neuronowej. Obliczanie przebiega wstecz przez sieć.

Zstępowanie gradientowe to iteracyjny algorytm optymalizacji służący do znajdowania minimum funkcji; w naszym przypadku chcemy zminimalizować funkcję błędu. Aby znaleźć lokalne minimum funkcji za pomocą zejścia gradientowego, wykonujemy kroki proporcjonalne do ujemnego gradientu funkcji w bieżącym punkcie.

Na przykład, aby zaktualizować w6, bierzemy bieżącą wartość w6 i odejmujemy częściową pochodną funkcji błędu względem w6. Opcjonalnie mnożymy pochodną funkcji błędu przez wybraną liczbę, aby upewnić się, że nowa zaktualizowana waga minimalizuje funkcję błędu; liczba ta nazywana jest współczynnikiem uczenia.

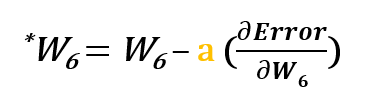
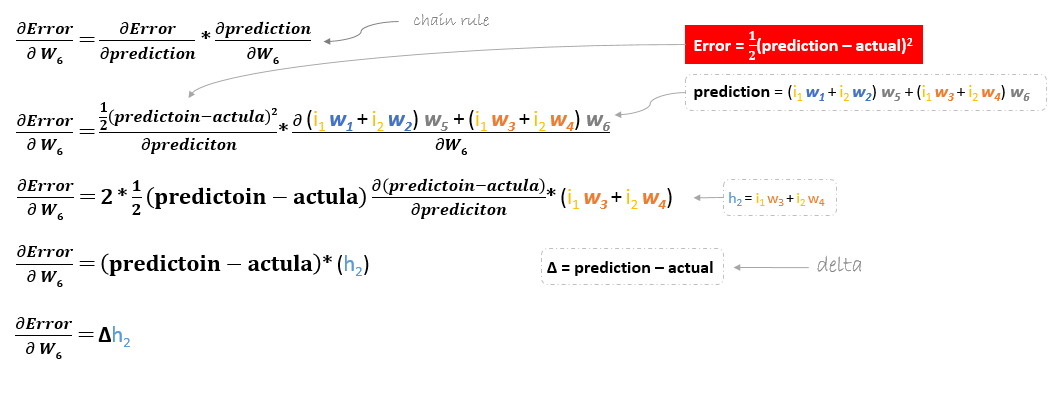
Pochodną funkcji błędu obliczamy stosując regułę łańcuchową w następujący sposób

Więc do aktualizacji w6 możemy zastosować następujący wzór

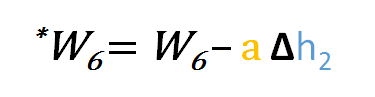
Podobnie możemy wyprowadzić wzór na aktualizację dla w5 i wszelkich innych wag istniejących pomiędzy warstwą wyjściową a ukrytą.

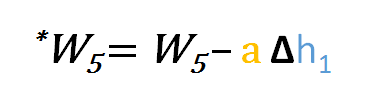
Jednakże podczas cofania się w celu aktualizacji w1w2w3 i w4 istniejących pomiędzy warstwą wejściową a ukrytą, pochodna cząstkowa dla funkcji błędu w odniesieniu do w1, na przykład, będzie następująca.

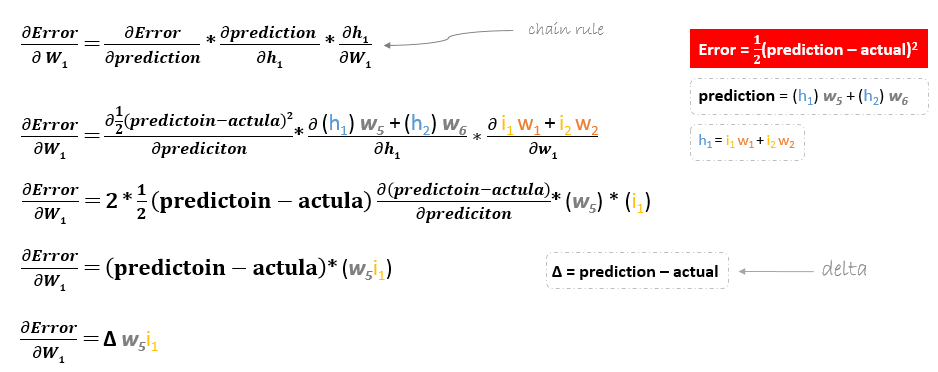
W ten sam sposób możemy znaleźć wzór aktualizacyjny dla pozostałych wag w2w3 i w4.

Podsumowując, formuły aktualizacji dla wszystkich wag będą wyglądały następująco:

Formuły aktualizacyjne w macierzach możemy przepisać w następujący sposób

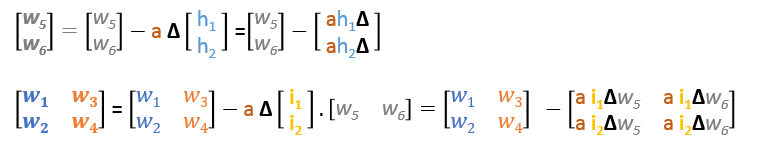
Przejście wstecz

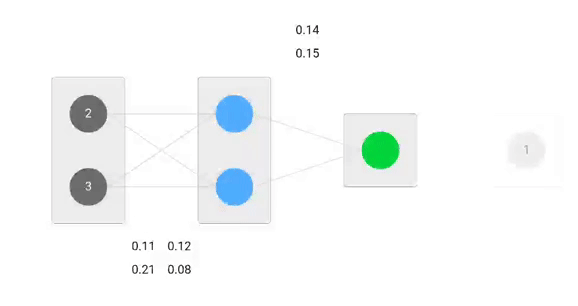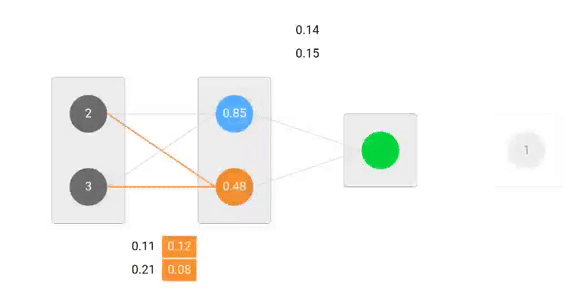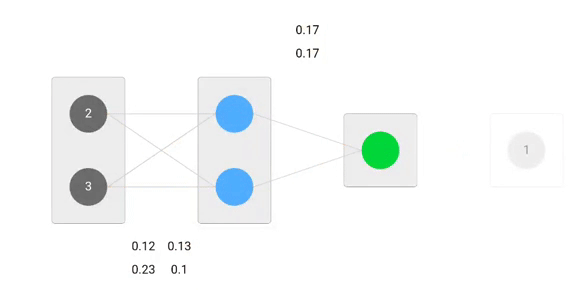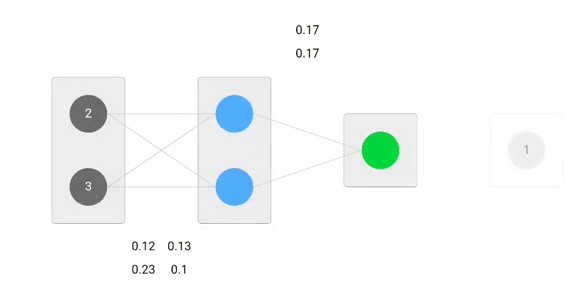
Używając wyprowadzonych wzorów możemy znaleźć nowe wagi.

Learning rate: jest hiperparametrem, co oznacza, że musimy ręcznie odgadnąć jego wartość.

Teraz, wykorzystując nowe wagi powtórzymy przejście do przodu

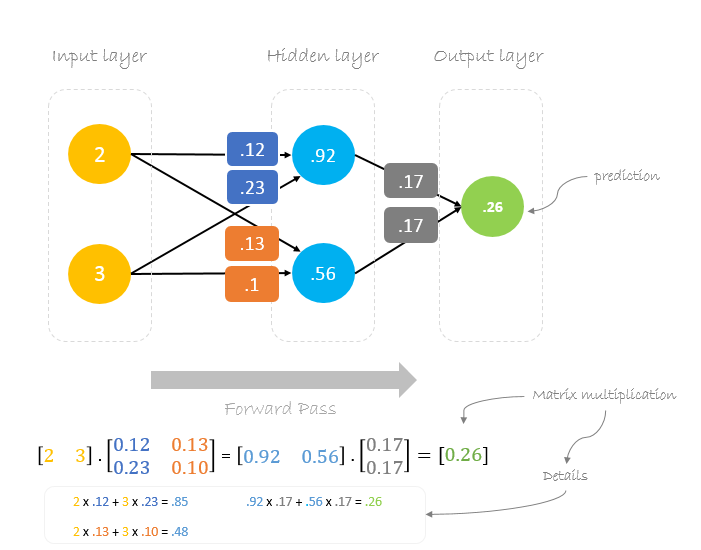
Możemy zauważyć, że predykcja 0.26 jest nieco bliższa rzeczywistej wartości wyjściowej niż poprzednio przewidywana 0.191. Możemy powtarzać ten sam proces przechodzenia wstecz i do przodu, aż błąd będzie bliski lub równy zeru.

Wizualizacja wstecznej propagacji

Możesz zobaczyć wizualizację przechodzenia do przodu i wstecznej propagacji tutaj.

Możesz zbudować swoją sieć neuronową używając netflow.js

Więcej informacji na temat sieci neuronowej można znaleźć na stronie.