Chang Hsin Lee

Kiedy buduję model uczenia maszynowego dla problemów klasyfikacji, jednym z pytań, które sobie zadaję jest dlaczego mój model nie jest do kitu? Czasami mam wrażenie, że tworzenie modelu jest jak trzymanie granatu, a kalibracja jest jedną z moich agrafek. W tym wpisie przedstawię koncepcję kalibracji, a następnie pokażę w Pythonie jak zrobić diagnostyczne wykresy kalibracyjne.

Tutaj link do notatnika Jupyter dla tego wpisu

Ocena przewidywań probabilistycznych

Zacznę od wyjaśnienia czym jest kalibracja i skąd wziął się ten pomysł.

W uczeniu maszynowym, większość modeli klasyfikacyjnych produkuje przewidywania prawdopodobieństwa klasy pomiędzy 0 a 1, a następnie ma możliwość przekształcenia probabilistycznych danych wyjściowych w przewidywania klasy. Nawet algorytmy, które produkują tylko wyniki, takie jak maszyna wektorów wspierających, mogą być zmodernizowane, aby produkować przewidywania podobne do prawdopodobieństwa.

Dla binarnego problemu klasyfikacji, istnieją metryki podsumowujące – dokładność, precyzja, przywołanie, F1-score i tak dalej – które oceniają jakość binarnych wyjść 0s i 1s. Jeśli dane wyjściowe nie są binarne, ale są liczbami zmiennopozycyjnymi pomiędzy 0 i 1, to mogę ich użyć jako wyników do rankingu. Ale liczby zmiennopozycyjne pomiędzy 0 a 1 krzyczą prawdopodobieństwem, a skąd mam wiedzieć, czy mogę im ufać jako prawdopodobieństwu?

Wyjście modelu może być postrzegane jako stwierdzenie mówiące, jak bardzo prawdopodobne jest, że coś się wydarzy. Przykładem takiego modelu – którego stwierdzenia sprawdzam codziennie przed wyjściem z domu – jest serwis pogodowy. W szczególności, jak prawdopodobne jest, że będzie padać?

image from weather.com

Wynika z niego, że w niedzielę jest 80% szans na deszcz. Jak bardzo wiarygodne jest to 80%? Jeśli zagłębię się w prognozy weather.com z przeszłości i okaże się, że 8 z 10 dni jest deszczowych, kiedy przewidują 80%, wtedy mogę przekonać się do załadowania audiobooków i przygotowania się na szalony ruch na autostradzie po południu.

Innymi słowy, dokładna prognoza pogody oznacza, że jeśli spojrzałem na 100 dni, które są przewidywane z 80% szansą na deszcz, to powinno być około 80 deszczowych dni. Musi być ona również dokładna w innych przedziałach prawdopodobieństwa. Dla dni, w których deszcz będzie padał przez 30% czasu, powinno być średnio 30 dni deszczowych na 100 dni. Jeśli wszystkie prognozy serwisu prognozującego pogodę są zgodne z tym dobrym wzorcem, to mówimy, że ich prognozy są skalibrowane. Jest to probabilistyczny sposób na powiedzenie, że trafiają w sedno.

• Model probabilistyczny jest skalibrowany, jeśli podzielę próbki testowe na kosze w oparciu o ich przewidywane prawdopodobieństwa, a prawdziwe wyniki każdego kosza mają proporcje zbliżone do prawdopodobieństw w koszu.

Jak ocenić kalibrację? Zamiast podsumowywać kalibrację do pojedynczej liczby, wolę robić wykresy kalibracji.

Wykresy kalibracji są często wykresami liniowymi. Kiedy już wybiorę liczbę koszy i wrzucę przewidywania do kosza, każdy kosz jest następnie przekształcany w kropkę na wykresie. Dla każdego kosza, wartość y jest proporcją prawdziwych wyników, a wartość x jest średnim przewidywanym prawdopodobieństwem. Dlatego dobrze skalibrowany model ma krzywą kalibracji, która pokrywa się z linią prostą y=x. Oto przykład wykresu kalibracyjnego z dwiema krzywymi, z których każda reprezentuje model na tych samych danych.

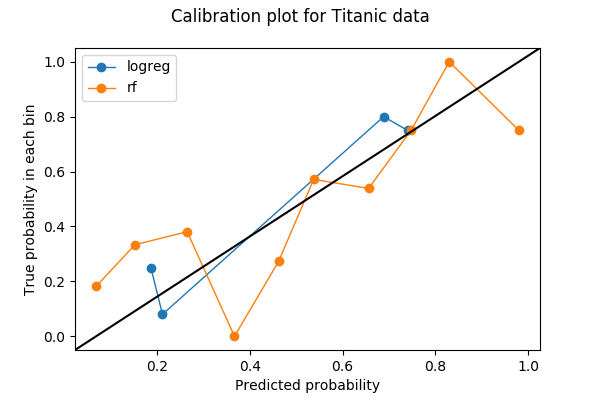
Pokażę, jak utworzyłem ten wykres w Pythonie i co w nim zobaczyłem.

Przykład w Pythonie

Pierwszą rzeczą jaką należy zrobić przy tworzeniu wykresu kalibracyjnego jest wybranie liczby binów. W tym przykładzie, podzieliłem prawdopodobieństwa na 10 koszy pomiędzy 0 a 1: od 0 do 0.1, 0.1 do 0.2, …, 0.9 do 1. Dane, których użyłem to zbiór danych Titanic z Kaggle, gdzie etykietą do przewidzenia jest zmienna binarna Survived.

Postaram się wykreślić krzywe kalibracyjne dla dwóch modeli – jednego dla regresji logistycznej, a drugiego dla lasu losowego. Oba modele produkują prawdopodobieństwa klas na Survived w oparciu o dwie cechy Age i Sex.

+----+------+--------+| Age| Sex|Survived|+----+------+--------+|22.0| male| 0||38.0|female| 1||26.0|female| 1|+----+------+--------+

Preprocessing

Przed wytrenowaniem moich modeli, wypełniłem brakujące wartości w Age jego średnią, a także zamieniłem Sex w zmienną numeryczną o wartościach 0 i 1.

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn import preprocessingfrom sklearn import model_selectiontitanic = pd.read_csv('train.csv')fitted_age_imputer = preprocessing.Imputer(axis=1).fit(titanic.values)titanic = fitted_age_imputer.transform( titanic.values.reshape(1, -1) ).transpose()titanic = np.where(titanic.Sex == 'female', 1, 0)

Następnie podzieliłem dane na zbiór treningowy i walidacyjny przez podział 80/20.

from sklearn import model_selectionfeature_cols = feature_train, feature_test, label_train, label_test = ( model_selection.train_test_split( titanic, titanic.Survived, test_size=0.2, random_state=1) )

Trenowanie i przewidywanie

Mogę teraz trenować model regresji logistycznej na moim zbiorze treningowym i przewidywać na zbiorze walidacyjnym.

from sklearn.linear_model import LogisticRegressionlogreg_model = LogisticRegression().fit(X=feature_train,y=label_train)logreg_prediction = logreg_model.predict_proba(feature_test)

Podobnie, wytrenuj model lasu losowego i przewiduj na zbiorze walidacyjnym.

from sklearn.ensemble import RandomForestClassifierrf_model = RandomForestClassifier(random_state=1234).fit(X=feature_train, y=label_train)rf_prediction = rf_model.predict_proba(feature_test)

Prawdopodobieństwo klasy pozytywnej jest zwracane przez modele w drugiej kolumnie (indeks=1):

logreg_prediction

array(, , , , ])

Wykres kalibracyjny

Gdy mam już prawdopodobieństwa klas i etykiety, mogę obliczyć biny dla wykresu kalibracyjnego. Tutaj używam sklearn.calibration.calibration_curve, który zwraca (x,y) współrzędne bloków na wykresie kalibracyjnym.

from sklearn.calibration import calibration_curvelogreg_y, logreg_x = calibration_curve(label_test, logreg_prediction, n_bins=10)

Zauważ, że chociaż poprosiłem o 10 bloków dla regresji logistycznej, 6 bloków z 10 nie ma żadnych danych. Powodem jest połączenie tego, że regresja logistyczna jest prostym modelem, że są tylko dwie cechy i że mam mniej niż 200 punktów danych w zestawie walidacyjnym.

), array()]

Następnie obliczam współrzędne dla bloków modelu random forest.

rf_y, rf_x = calibration_curve(label_test, rf_prediction, n_bins=10)

Teraz mogę wykreślić dwie krzywe kalibracyjne. Aby ułatwić odczytanie fabuły, dodałem również linię odniesienia y=x w oparciu o odpowiedź StackOverflow.

%matplotlib inlineimport matplotlib.pyplot as pltimport matplotlib.lines as mlinesimport matplotlib.transforms as mtransformsfig, ax = plt.subplots()# only these two lines are calibration curvesplt.plot(logreg_x,logreg_y, marker='o', linewidth=1, label='logreg')plt.plot(rf_x, rf_y, marker='o', linewidth=1, label='rf')# reference line, legends, and axis labelsline = mlines.Line2D(, , color='black')transform = ax.transAxesline.set_transform(transform)ax.add_line(line)fig.suptitle('Calibration plot for Titanic data')ax.set_xlabel('Predicted probability')ax.set_ylabel('True probability in each bin')plt.legend()plt.show()

Całości binów i dyskryminacja

Dla regresji logistycznej są tylko 4 niepuste kosze, gdy prosiłem o 10 koszy. Czy to coś złego? Użyjmy funkcji, którą zaczerpnąłem z kodu źródłowego sklearn.calibration.calibration_curve, aby dowiedzieć się, które z nich są brakującymi binami.

def bin_total(y_true, y_prob, n_bins): bins = np.linspace(0., 1. + 1e-8, n_bins + 1) # In sklearn.calibration.calibration_curve, # the last value in the array is always 0. binids = np.digitize(y_prob, bins) - 1 return np.bincount(binids, minlength=len(bins))bin_total(label_test, logreg_prediction, n_bins=10)

array(, dtype=int64)

Brakujące kosze mają wartości środkowe 5%, 35%, 45%, 55%, 85% i 95%. W rzeczywistości posiadanie niskich wartości całkowitych lub pustych koszy w środkowych koszach (30-60%) może być w rzeczywistości dobrą rzeczą – chcę, aby moje przewidywania unikały tych środkowych koszy i stały się dyskryminujące.

Dyskryminacja jest koncepcją, która idzie obok kalibracji w problemach klasyfikacyjnych. Czasami pojawia się przed kalibracją, jeśli celem budowania modelu jest podejmowanie automatycznych decyzji, a nie dostarczanie szacunków statystycznych. Wyobraźmy sobie scenariusz, w którym mam dwa modele pogodowe i mieszkam w Podunk, Nevada, gdzie 10% (36 dni w roku) dni jest deszczowych:

• Model A zawsze mówi, że jest 10% szans na deszcz bez względu na to, który to dzień.
• Model B mówi, że będzie padać codziennie w czerwcu (100%), a nigdy nie pada w pozostałych 11 miesiącach (0%).

Model A jest doskonale skalibrowany. Jest tylko jeden przedział – przedział 10% – a prawdziwe prawdopodobieństwo wynosi 10%. Model B, jednak, jest nieco wyłączony w kalibracji, ponieważ będzie 30 dni w 100% bin, ale także 6 deszczowych dni w 0% bin. Jednak model B jest wyraźnie bardziej użyteczny, jeśli robię plany na weekendowe wędrówki. Model B jest bardziej dyskryminacyjny niż A, ponieważ łatwiej jest podejmować decyzje (wędrówka/nie wędrówka) w oparciu o dane wyjściowe modelu B.

Dyskryminacja jest często sprawdzana za pomocą krzywych charakterystyki operacyjnej odbiornika, lub krzywych ROC, ale to temat na inny wpis.

Walidacja krzyżowa?

Jeśli nie dbam o dyskryminację i chcę tylko dobrej kalibracji, to regresja logistyczna (niebieska) wydaje się być lepsza niż las losowy (pomarańczowa). Czy tak jest w rzeczywistości? W szczególności, jeśli spojrzę na liczbę punktów w binach dla losowego lasu,

bin_total(label_test, rf_prediction, n_bins=10)

array(, dtype=int64)

Podejrzewam, że problem może polegać na tym, że niektóre biny mają zbyt mało punktów danych. Umieściłem 200 punktów w 10 koszach, więc niektóre kosze dostaną tylko kilka, dlatego działka kalibracyjna cierpi, ponieważ jedna błędna klasyfikacja w maleńkim koszu bardzo zmienia proporcje.

Tylko 20% moich danych zostało wykorzystanych w poprzedniej działce, więc może mogę użyć więcej. Aby wykorzystać wszystkie moje dane w testowaniu kalibracji między różnymi modelami, pomyślałem, że mogę ukraść pomysł z walidacji krzyżowej. Jeśli podzielę moje dane na 5 fałd do walidacji krzyżowej, to każda fałda będzie używana jako zestaw walidacyjny raz. Dlatego mogę połączyć przewidywane prawdopodobieństwa z wszystkich 5 fałd i utworzyć z nich wykres kalibracyjny. Wynikiem 5-krotnego wykresu kalibracyjnego jest poniższy wykres. Kod można znaleźć w ostatniej sekcji notatnika Jupyter.

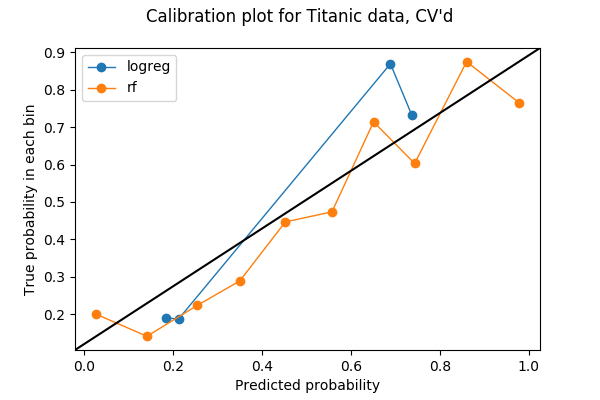
Każdy kosz ma teraz więcej punktów:

array(, dtype=int64)

i myślę, że można bezpiecznie powiedzieć, że w tym przykładzie las losowy jest lepiej skalibrowany niż regresja logistyczna.

***

Nate Silver ma świetny przykład na temat kalibracji pogody w książce The Signal and the Noise, gdzie badał prognozy z trzech źródeł – National Weather Service, the Weather Channel i lokalne kanały informacyjne – w rozdziale 4, For Years You’ve Been Telling Us That Rain Is Green. Doszedł do wniosku, że większość lokalnych kanałów informacyjnych jest źle skalibrowana i jest „mokra”. To klejnot i polecam podnieść książkę, jeśli możesz dostać rękę na nim.

Po raz pierwszy dowiedziałem się o kalibracji przez mojego kolegę Kevina w 2016 roku, kiedy omówiliśmy kilka metryk na modelach klasyfikacyjnych. Bez niego prawdopodobnie zajmie mi to kolejny rok lub dwa, zanim uświadomię sobie znaczenie kalibracji, a znacznie później przed napisaniem tego posta.