Articles

College Algebra

19 września, 2020 /

Wskazówki do nauczenia się

  • Konwersja z postaci logarytmicznej na wykładniczą.
  • Konwersja z postaci wykładniczej na logarytmiczną.

Aby analizować wielkość trzęsień ziemi lub porównywać wielkości dwóch różnych trzęsień ziemi, musimy być w stanie konwertować między formą logarytmiczną i wykładniczą. Na przykład, załóżmy, że ilość energii uwolnionej z jednego trzęsienia ziemi była 500 razy większa niż ilość energii uwolnionej z innego trzęsienia ziemi. Chcemy obliczyć różnicę w magnitudzie. Równanie, które reprezentuje ten problem to {10}^{x}=500, gdzie x reprezentuje różnicę w magnitudach w skali Richtera. Jak rozwiązalibyśmy x?

Nie poznaliśmy jeszcze metody algebraicznego rozwiązywania równań wykładniczych. Żadne z omówionych do tej pory narzędzi algebraicznych nie wystarczy do rozwiązania równania {10}^{x}=500. Wiemy, że {10}^{2}=100 i {10}^{3}=1000, więc jasne jest, że x musi być jakąś wartością pomiędzy 2 a 3, skoro y={10}^{x} jest rosnące. Możemy przeanalizować wykres, aby lepiej oszacować rozwiązanie.

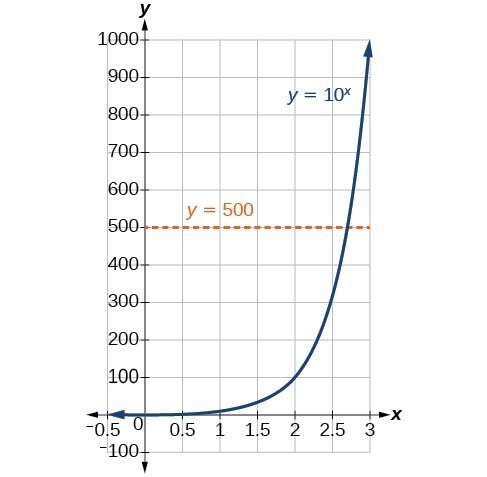
Grafik przecięć równań y=10^x i y=500.

Oszacowanie na podstawie wykresu jest jednak nieprecyzyjne. Aby znaleźć rozwiązanie algebraiczne, musimy wprowadzić nową funkcję. Zauważmy, że powyższy wykres przechodzi test linii poziomej. Funkcja wykładnicza y={b}^{x} jest jedynkowa, więc jej odwrotność, x={b}^{y} jest również funkcją. Jak w przypadku wszystkich funkcji odwrotnych, po prostu zamieniamy x i y i rozwiązujemy dla y, aby znaleźć funkcję odwrotną. Aby przedstawić y jako funkcję x, używamy funkcji logarytmicznej w postaci y={b}_lewa(x-prawa). Logarytm o podstawie b danej liczby to wykładnik, o który musimy podnieść b, aby otrzymać tę liczbę.

Wyrażenie logarytmiczne odczytujemy jako, „Logarytm o podstawie b z x jest równy y” lub, w uproszczeniu, „logarytm o podstawie b z x to y”. Możemy również powiedzieć: „b podniesione do potęgi y to x”, ponieważ logarytmy są wykładnikami. Na przykład, logarytm podstawy 2 z 32 to 5, ponieważ 5 jest wykładnikiem, który musimy zastosować do 2, aby otrzymać 32. Ponieważ {2}^{5}=32, możemy napisać {{2}^{log}}_{2}32=5. Odczytujemy to jako „podstawa logiczna 2 z 32 wynosi 5.”

Zależność między formą logarytmiczną a odpowiadającą jej formą wykładniczą możemy wyrazić w następujący sposób:

{mathrm{log}_{b} lewa(x}prawa)=y} lewa_prawa {b}^{y}=x,\tekst{b>0,b 1

Zauważ, że podstawa b jest zawsze dodatnia.

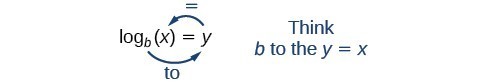
Pomyśl, że b w stosunku do y równa się x.

Ponieważ logarytm jest funkcją, najpoprawniej jest zapisać go jako {{mathrm{log}}_{b}}left(x}right) używając nawiasów do oznaczenia oceny funkcji, tak samo jak w przypadku f}left(x}right). Jednakże, gdy dane wejściowe są pojedynczą zmienną lub liczbą, często zdarza się, że opuszczamy nawiasy i wyrażenie zapisujemy bez nawiasów jako {{mathrm{log}}_{b}x. Zauważ, że wiele kalkulatorów wymaga nawiasów wokół x.

Możemy zilustrować notację logarytmów w następujący sposób:

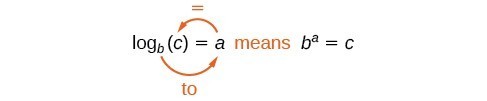
logb (c) = a oznacza, że b do potęgi A równa się C.

Zauważ, że przy porównywaniu funkcji logarytmu i funkcji wykładniczej, wejście i wyjście są zamienione. Oznacza to, że y={mathrm{log}}_{b} lewa(x) prawa) i y={b}^{x} są funkcjami odwrotnymi.

Uwaga ogólna: Definicja funkcji logarytmicznej

Podstawa logarytmu b liczby dodatniej x spełnia następującą definicję:

Dla x>0,b>0,b 1,

y={mathrm{log}}_{b}}_lewa(x}prawa)^{y} jest równy }{b}^{y}=x, gdzie

  • czytamy {{mathrm{log}}_{b}}left(x}right) jako, „logarytm o podstawie b z x” lub „log podstawa b z x.”
  • logarytm y jest wykładnikiem, do którego należy podnieść b, aby otrzymać x.
  • jeśli nie podano podstawy b, przyjmuje się, że podstawa logarytmu wynosi 10.

Ponadto, ponieważ funkcje logarytmiczna i wykładnicza zamieniają wartości x i y, dziedzina i zakres funkcji wykładniczej są zamienione na funkcję logarytmiczną. Dlatego,

  • dziedzina funkcji logarytmicznej o podstawie b jest} \left(0,\infty \right).
  • działka funkcji logarytmicznej o podstawie b jest} \left(-infty ,\infty \right).

Q & A

Czy możemy przyjąć logarytm liczby ujemnej?

Nie. Ponieważ podstawa funkcji wykładniczej jest zawsze dodatnia, żadna potęga tej podstawy nigdy nie może być ujemna. Nigdy nie możemy przyjąć logarytmu z liczby ujemnej. Nie możemy również przyjąć logarytmu zera. Kalkulatory mogą wyświetlać log liczby ujemnej, gdy są w trybie złożonym, ale log liczby ujemnej nie jest liczbą rzeczywistą.

Jak to zrobić: Biorąc pod uwagę równanie w postaci logarytmicznej {{b}} lewa(x) prawa)=y, przekształć je do postaci wykładniczej

  1. Zbadaj równanie y={mathrm{log}}_{b}x i zidentyfikuj b, y, i x.
  2. Zapisz ponownie {{mathrm{log}}_{b}x=y jako {b}^{y}=x.

Przykład: Converting from Logarithmic Form to Exponential Form

Zapisz następujące równania logarytmiczne w postaci wykładniczej.

  1. {mathrm{log}_{6}}left(ąqrt{6}}right)=frac{1}{2}
  2. {mathrm{log}_{3}}left(9}right)=2
Pokaż rozwiązanie

Pierwsze, zidentyfikuj wartości b, y i x. Następnie zapisz równanie w postaci {b}^{y}=x.

  1. {mathrm{log}}_{6}}lewa(∗qrt{6}}prawa)={frac{1}{2}. Tutaj, b=6,y=frac{1}{2},\tekst{i} x=sqrt{6}. Zatem równanie {{mathrm{log}}_{6}}lewa(\sqrt{6}prawa)= = {6}^{\sqrt{1}{2}}} jest równe {6}^{\sqrt{6}}.
  2. {mathrm{log}_{3}}lewa(9}prawa)=2 Tutaj b = 3, y = 2, i x = 9. Zatem równanie {{mathrm{log}_{3}}left(9}right)=2 jest równe {3}^{2}=9.

Try It

Pisz następujące równania logarytmiczne w postaci wykładniczej.

  1. {mathrm{log}}_{10}}left(1,000,000} prawo)=6
  2. {mathrm{log}_{5} lewo(25} prawo)=2
Pokaż rozwiązanie

  1. {mathrm{log}_{10} lewo(1,000,000)=6 jest równe {10}^{6}=1,000,000
  2. {mathrm{log}_{5}}left(25}right)=2 jest równe {5}^{2}=25

Konwersja z postaci wykładniczej na logarytmiczną

Aby przekonwertować z postaci wykładniczej na logarytmiczną, wykonujemy te same kroki w odwrotnej kolejności. Określamy podstawę b, wykładnik x i wynik y. Następnie piszemy x={{mathrm{log}_{b}} lewa strona(y prawa strona).

Przykład: Converting from Exponential Form to Logarithmic Form

Zapisz następujące równania wykładnicze w postaci logarytmicznej.

  1. {2}^{3}=8
  2. {5}^{2}=25
  3. {10}^{-4}=frac{1}{10,000}
Pokaż rozwiązanie

Po pierwsze, zidentyfikuj wartości b, y, i x. Następnie zapisz równanie w postaci x={mathrm{log}_{b}}lewa(y) prawa.

  1. {2}^{3}=8 Tutaj b = 2, x = 3, a y = 8. Zatem równanie {2}^{3}=8 jest równe {{mathrm{log}}_{2}}left(8}right)=3.
  2. {5}^{2}=25 Tutaj b = 5, x = 2, a y = 25. Zatem równanie {5}^{2}=25 jest równe {{mathrm{log}}_{5}}}left(25}right)=2.
  3. {10}^{-4}={frac{1}{10,000} Tutaj b = 10, x = -4, i y={frac{1}{10,000}. Zatem równanie {10}^{-4}=frac{1}{10,000} jest równe {text{log}_{10}}left(\frac{1}{10,000}}right)=-4.

Try It

Pisz następujące równania wykładnicze w postaci logarytmicznej.

  1. {3}^{2}=9
  2. {5}^{3}=125
  3. {2}^{-1}=frac{1}{2}
Pokaż rozwiązanie

  1. {3}^{2}=9 jest równe {{mathrm{log}}_{3}}left(9}right)=2
  2. {5}^{3}=125 jest równe {{mathrm{log}}_{5}}}left(125}right)=3
  3. {2}^{-1}=1}{2} jest równe {{text{log}_{2}}left(\frac{1}{2}}}right)=-1

Przykład!

Masz pomysł na ulepszenie tej zawartości? Chętnie poznamy Twój wkład.

Ulepsz tę stronęDowiedz się więcej

Dodaj komentarz

Twój adres email nie zostanie opublikowany. Pola, których wypełnienie jest wymagane, są oznaczone symbolem *