Faktor

Co to jest czynnik?

Faktor (oznaczany lub przedstawiany jako n!) dla liczby dodatniej lub liczby całkowitej (która jest oznaczana przez n) jest iloczynem wszystkich liczb dodatnich poprzedzających lub równoważnych n (dodatnia liczba całkowita). Funkcję czynnikową można znaleźć w różnych dziedzinach matematyki, w tym w algebrze, analizie matematycznej i kombinatoryce.

Począwszy od 1200 roku, czynnikowe były używane do liczenia permutacji. Notacja dla czynnika (n!) została wprowadzona na początku 1800 roku przez Christiana Krampa, francuskiego matematyka.

Wzór na czynnik można zobaczyć poniżej:

Definicja faktora

Funkcją faktora jest iloczyn wszystkich liczb całkowitych dodatnich poprzedzających i/lub równych n, czyli:

n! = 1 ∙ 2 ∙ 3 ∙∙ (n – 2) ∙ (n – 1) ∙ n,

gdy patrzymy na wartości lub liczby całkowite większe lub równe 1. Można to zapisać jako:

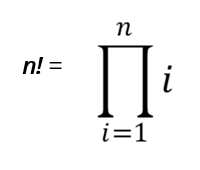
Powyższe równanie zapisane zgodnie z notacją iloczynu pi, daje w efekcie zależność rekurencyjną widoczną poniżej:

n! = n ∙ (n – 1) !.

Kilka przykładów zastosowania tej notacji można zobaczyć poniżej:

• 4! = 4 ∙ 3!
• 7! = 7 ∙ 6!
• 80! = 80 ∙ 79! itd.

Tablica czynnikowa

Poniższa tabela zawiera przegląd czynników dla liczb całkowitych z przedziału od 0 do 10:

Faktoriał 0 (zero)

Powszechnie wiadomo, że czynnik 0 jest równy 1 (jeden). Można go oznaczyć jako:

0! = 1

Istnieje kilka powodów uzasadniających powyższy zapis i definicję. Po pierwsze, definicja pozwala na zwięzłe wyrażenie znacznej liczby wzorów, w tym funkcji wykładniczej, oraz tworzy rozszerzenie relacji rekurencji na 0.

W dodatku, gdy n = 0, definicja jego czynnika (n!) obejmuje iloczyn zerowy liczb, czyli jest równoważna tożsamości mnożenia w szerszym ujęciu.

Ponadto, definicja czynnika zerowego obejmuje tylko jedną permutację obiektów zerowych lub zerowych. Wreszcie, definicja ta potwierdza również wiele tożsamości w kombinatoryce.

Definicje, na które należy zwrócić uwagę w odniesieniu do czynnika zerowego

• Kombinatoryka: Obszar w matematyce, który koncentruje się na liczeniu.
• Permutacja: W matematyce, permutacja odnosi się do układu członków zbioru w porządku liniowym lub sekwencji.
• Relacja rekursji: Relacja rekursji, w matematyce, odnosi się do równania, które definiuje sekwencję lub rozległą tablicę wartości, rekurencyjnie. Rekursja oznacza definiowanie czegoś w kategoriach tego samego.

Różne zastosowania funkcji czynnikowej

Funkcję czynnikową można znaleźć w różnych dziedzinach matematyki. Po pierwsze, istnieje n! wyróżnionych sposobów na ułożenie n konkretnych obiektów w ciąg. Ponadto, faktory mogą być użyte do uwzględnienia nieznajomości lub nieuwzględnienia uporządkowania we wzorze, służąc jako mianownik.

Faktory występują również w algebrze poprzez twierdzenie dwumianowe oraz w rachunku, gdzie występują w mianownikach wzoru Taylora. Ponadto, czynnik można znaleźć w teoriach prawdopodobieństwa i liczb i mogą one być używane do umożliwienia manipulacji wyrażeń.

Inne ciągi podobne do czynnika

W matematyce, istnieje wiele ciągów, które są porównywalne do czynnika. Należą do nich:

• Faktory podwójne, które są używane do upraszczania całek trygonometrycznych.
• Faktory wieloczynnikowe, które mogą być oznaczane wieloma wykrzyknikami.
• Faktory pierwotne, które pociągają za sobą otrzymanie iloczynu liczb pierwszych, które są mniejsze lub równe n.
• Superfaktoriale, które definiuje się jako iloczyn pierwszych n factoriali.
• Hiperfaktoriale, które są wynikiem mnożenia kilku kolejnych wartości z zakresu od 1 do n.

Dodatkowe zasoby

CFI jest oficjalnym dostawcą globalnej akredytacji Commercial Banking & Credit Analyst (CBCA)™CBCA™ CertificationThe Commercial Banking & Credit Analyst (CBCA)™ accreditation is a global standard for credit analysts that covers finance, księgowość, analizę kredytową, analizę przepływów pieniężnych, modelowanie kowenantów, spłatę kredytów i inne. Program certyfikacji, zaprojektowany tak, aby pomóc każdemu stać się światowej klasy analitykiem finansowym. Aby kontynuować rozwój swojej kariery, dodatkowe zasoby CFI poniżej będą przydatne:

• Macierz korelacjiMacierz korelacjiMacierz korelacji to po prostu tabela, która wyświetla współczynniki korelacji dla różnych zmiennych. Macierz przedstawia korelację pomiędzy wszystkimi możliwymi parami wartości w tabeli. Jest to potężne narzędzie do podsumowania dużego zbioru danych oraz do identyfikacji i wizualizacji wzorców w danych.
• Matematyka finansowaMatematyka finansowa opisuje zastosowanie matematyki i modelowania matematycznego do rozwiązywania problemów finansowych. czasami jest określana jako
• Analitycy ilościowiAnalitycy ilościowi (zwani również „quants”) są profesjonalistami specjalizującymi się w projektowaniu, rozwoju i wdrażaniu algorytmów i modeli matematycznych lub statystycznych przeznaczonych do rozwiązywania złożonych problemów finansowych. W swojej pracy analitycy ilościowi stosują mieszankę technik i wiedzy
• Rozkład standardowyRozkład próbkowaniaRozkład próbkowania odnosi się do rozkładu prawdopodobieństwa statystyki, która pochodzi z wyboru losowych próbek z danej populacji

.