Odwrócenie macierzy: Finding the Inverse of a Matrix

Powrót do Indeksu Lekcji | Wykonaj Lekcje w Kolejności | Strona przyjazna do drukowania

Odwrócenie macierzy:najdowanie odwrotności macierzy (strona 1 z 2)

W przypadku macierzy nie ma czegoś takiego jak dzielenie. Możesz dodawać, odejmować i mnożyć macierze, ale nie możesz ich dzielić. Istnieje jednak powiązana koncepcja, która nazywa się „inwersją”. Najpierw omówię, dlaczego inwersja jest przydatna, a następnie pokażę, jak to zrobić.

Pomyśl o tym, kiedy po raz pierwszy nauczyłeś się rozwiązywać równania liniowe. Jeśli otrzymałeś coś takiego jak „3x = 6”, rozwiązałbyś to dzieląc obie strony przez 3. Ponieważ mnożenie przez1/3 jest takie samo jak dzielenie przez 3, mógłbyś również pomnożyć obie strony przez 1/3, aby uzyskać tę samą odpowiedź: x = 2. Jeśli musiałbyś rozwiązać coś takiego jak „(3/2)x = 6”, nadal mógłbyś podzielić obie strony przez 3/2, ale prawdopodobnie łatwiej byłoby pomnożyć obie strony przez 2/3. Odwrotność ułamka 2/3 jest odwrotnością 3/2, ponieważ jeśli pomnożysz te dwa ułamki, otrzymasz 1, co w tym kontekście nazywane jest „tożsamością (multiplikatywną)”: 1 jest nazywane tożsamością, ponieważ mnożenie czegoś przez 1 nie zmienia jego wartości.

Ta terminologia i te fakty są bardzo ważne dla macierzy. Jeśli otrzymasz równanie macierzowe, takie jak AX = C, gdzie masz A i C i powiedziano ci, aby obliczyć X, chciałbyś „oddzielić” macierz A. Ale nie możesz wykonać podziału z macierzami. Z drugiej strony, co by było, gdybyś mógł znaleźć odwrotność A, coś podobnego do znalezienia odwrotności ułamka powyżej? Odwrotność A, zapisana jako „A-1” i wymawiana jako „A inverse”, pozwoliłaby Ci anulować A z równania macierzowego, a następnie rozwiązać dla X.

AX = C
A-1AX = A-1C
IX = A-1C
X = A-1C

Jak „A-1AX” po lewej stronie równania zamieniło się w „X”? Wróćmy do natury odwrotności dla zwykłych liczb. Jeśli masz liczbę (taką jak 3/2) i jej odwrotność (w tym przypadku, 2/3) i pomnożysz je, otrzymasz 1. A 1 jest tożsamością, tak zwaną, ponieważ 1x = x dla dowolnej liczby x. To działa w ten sam sposób dla macierzy. Jeśli pomnożysz macierz (taką jak A) i jej odwrotność (w tym przypadku,
A-1), otrzymasz macierz tożsamości I. A sensem macierzy tożsamości jest to, że IX = X dla dowolnej macierzy X (co oznacza „dowolną macierz o odpowiednim rozmiarze”, oczywiście).

Należy zauważyć, że kolejność w powyższym mnożeniu jest ważna i nie jest wcale dowolna. Przypomnijmy, że w przypadku macierzy, mnożenie nie jest komutatywne. Oznacza to, że AB prawie nigdy nie jest równe BA. Tak więc mnożenie równania macierzowego „po lewej stronie” (aby otrzymać A-1AX) nie jest wcale tym samym, co mnożenie „po prawej stronie” (aby otrzymać AXA-1). I nie można powiedzieć, że produkt AXA-1 jest równy A-1AX, ponieważ nie można zmienić kolejności w mnożeniu. Zamiast tego musisz pomnożyć A-1 po lewej stronie, umieszczając go tuż obok A w oryginalnym równaniu macierzy. A ponieważ musisz zrobić to samo po obu stronach równania podczas rozwiązywania, musisz mnożyć „po lewej stronie” po prawej stronie równania, co daje A-1C. Nie możesz być przypadkowy w rozmieszczaniu macierzy; musisz być precyzyjny, poprawny i konsekwentny. To jest jedyny sposób, aby skutecznie anulować A i rozwiązać równanie macierzowe.

Jak widać powyżej, macierze odwrotne mogą być bardzo przydatne do rozwiązywania równań macierzowych. Ale, biorąc pod uwagę macierz, jak ją odwrócić? Jak znaleźć jej odwrotność? Technika odwracania macierzy jest dość sprytna. Dla danej macierzy A i jej odwrotności A-1, wiemy, że mamy A-1A = I. Będziemy używać macierzy tożsamości I w procesie odwracania macierzy.

• Znajdź odwrotność następującej macierzy.

Najpierw zapisuję pozycje macierzy A, ale zapisuję je w macierzy o podwójnej szerokości:

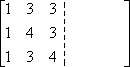
W drugiej połowie macierzy podwójnie szerokiej zapisuję macierz tożsamości:

Teraz wykonam operacje na rzędach macierzy, aby przekształcić lewą stronę podwójnej szerokości w tożsamość. (Jak zawsze w przypadku operacji na rzędach, nie ma jednego „właściwego” sposobu, aby to zrobić. To, co następuje, to tylko kroki, które przyszły mi do głowy. Twoje obliczenia mogą łatwo wyglądać zupełnie inaczej.)

Teraz, gdy lewa strona podwójnej szerokości zawiera tożsamość, prawa strona zawiera odwrotność. To znaczy, macierz odwrotna jest następująca:

Zauważ, że możemy potwierdzić, że ta macierz jest odwrotnością A, mnożąc obie macierze i potwierdzając, że otrzymujemy tożsamość: Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved

Uwaga: w „prawdziwym życiu” odwrotność rzadko jest macierzą wypełnioną ładnymi, schludnymi liczbami całkowitymi, jak ta. Przy odrobinie szczęścia, zwłaszcza jeśli wykonujesz odwrotności ręcznie, będziesz miał do wykonania takie ładne macierze jak ta.

Top | 1 | 2 | Return to Index Next >>