Rozciąganie poziome – własności, wykres i przykłady
Mogłeś już spotkać się z wykresami, które wyglądają podobnie, ale mają różne szerokości. Funkcje te mogły zostać poziomo rozciągnięte przy użyciu funkcji bazowej. Rozciąganie poziome jest jedną z najczęściej stosowanych technik transformacji podczas tworzenia wykresów funkcji, więc najlepiej jest zrozumieć jej definicję.
Rozciąganie poziome ma miejsce, gdy wykres bazowy jest rozszerzany wzdłuż osi x i z dala od osi y.
Poznanie, jak możemy rozciągać wykresy w poziomie, może pomóc nam zrozumieć rodzinę wykresów funkcji. Możemy również nauczyć się, jak przyspieszyć tworzenie wykresów nowych funkcji w oparciu o zastosowane współczynniki skali.
Pamiętaj, aby przejrzeć swoją wiedzę na temat funkcji macierzystych, translacji i rozciągnięć pionowych przed przejściem do następnej sekcji.
- Zrozumienie typowych funkcji macierzystych, które możemy napotkać.
- Odśwież swoją wiedzę na temat transformacji pionowych i poziomych.
- Przejrzyj, jak stosujemy rozciągnięcia pionowe.
Podlinkowane artykuły mogą pomóc Ci odświeżyć wiedzę, a kiedy będziesz gotowy, przejdźmy dalej i dowiedzmy się więcej o rozciąganiu poziomym.
Co to jest rozciągnięcie poziome?
Możemy zastosować rozciąganie poziome do funkcji poprzez pomnożenie jej wartości wejściowych przez współczynnik skali, a, gdzie 0 < 1/a < 1. Co to oznacza dla funkcji takich jak f(x)? Gdy 1/a jest mnożone przez x, wykres f(x) rozciąga się poziomo o współczynnik skali a.
Popatrzmy dalej, jak na f(x) = x2 wpłynie współczynnik skali 1/2 i 1/3.
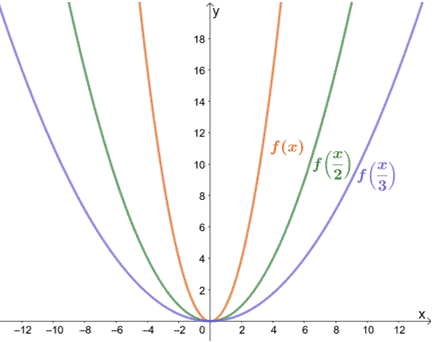
Jak się spodziewaliśmy, wykres rozciąga się o współczynnik 2 i 3. Zauważ, że wartości y pozostają takie same? Jest to prawdą dla wszystkich poziomych rozciągnięć. Wykres rozciąga się tylko od osi y, gdy rozciągamy go poziomo.
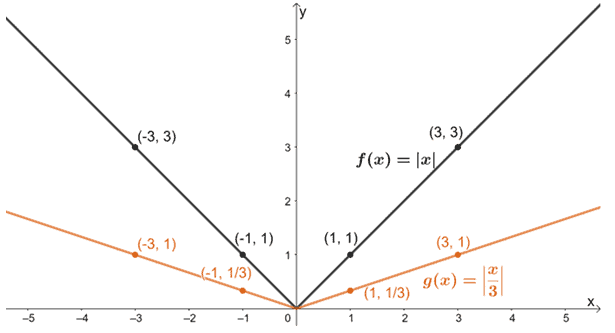
Poziome rozciąganie innych funkcji będzie miało podobne właściwości. Załóżmy, że mamy f(x) = |x|, jeśli wykres tej funkcji ma być rozciągnięty poziomo, aby uzyskać g(x), to nowe wyrażenie funkcji może być wyrażone jako |1/3 ∙ x| = |x/3|.
Dlaczego nie porównamy pewnych wartości z obu funkcji?
| x | -2 | -1 | 0 | 1 | 2 |
| f(x) = |x| | 2 | 1 | 0 | 1 | 2 |
Oczekujemy również, że wszystkie jego współrzędne x-.mają wzrosnąć o 3. Kiedy to zrobimy, wartości wyjściowe pozostaną takie same.
| x | -6 | -.3 | 0 | 3 | 6 |
| g(x) = |x/3| | 2 | 1 | 0 | 1 | 2 |
Co to oznacza dla współrzędnych wykresu nowej funkcji? Jeśli funkcja f(x) przechodzi przez (m, n) i jest rozciągnięta poziomo o współczynnik 1/a, to nowa funkcja będzie przechodzić przez (am, n).
Jak poziomo rozciągnąć funkcję?
Jak już dowiedzieliśmy się o poziomych rozciągnięciach i jak wpływają one na funkcję bazową, nadszedł czas, abyśmy zastosowali je na wykresach funkcji. Zanim zaczniemy rozciągać funkcje poziomo o określony współczynnik, zapamiętaj te wskazówki, aby szybciej rozciągać wykresy poziomo:
- Tylko rozciągaj podstawę wykresu poziomo, tak aby współrzędne y pozostały w tej samej pozycji.
- Ponieważ współrzędne y pozostaną takie same, punkt przecięcia y również pozostanie taki sam.
- Pamiętaj, aby dwukrotnie sprawdzić krytyczne punkty na wykresie, takie jak punkty przecięcia, punkty maksymalne i inne.
- Sprawdź, czy punkty współrzędnych są skalowane poprawnie.
Użyjmy tabeli wartości pokazanej w poprzedniej sekcji do sporządzenia wykresów y = |x| i y = |x/3|, aby zwizualizować efekty poziomego rozciągnięcia wykresu.
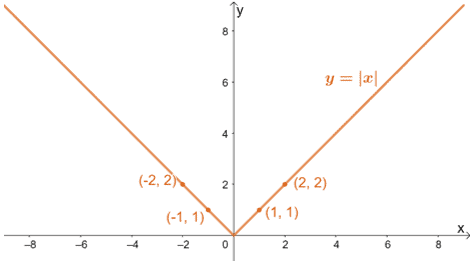
Jak już mówiliśmy, oczekujemy, że wykresy będą się rozciągać wzdłuż podstawy, przy czym wartości y pozostaną stałe.
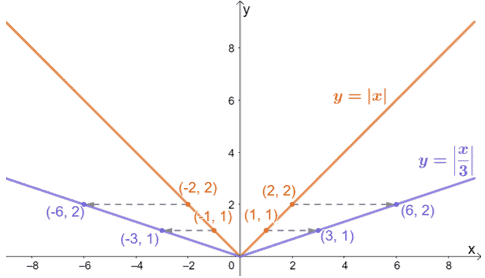
Aby uzyskać y = |x/3|, rozciągamy funkcję nadrzędną y = |x| o współczynnik 3. Powyższy wykres to potwierdza, a ten sam proces możemy zastosować przy poziomym rozciąganiu wykresów innych funkcji.
Gotowi do wykreślania kolejnych funkcji i stosowania poziomych rozciągnięć? Podsumujmy to, czego nauczyliśmy się do tej pory, zanim spróbujemy odpowiedzieć na kolejne pytania.
Podsumowanie definicji i własności rozciągnięcia poziomego
Oto kilka ważnych wskazówek, o których należy pamiętać, odpowiadając na zadania i sporządzając wykresy funkcji, które wymagają rozciągnięcia poziomego:
- Możemy poziomo rozciągnąć wykres o współczynnik 1/a tylko wtedy, gdy wartość wejściowa jest również zwiększona o a.
- Gdy f(x) jest rozciągnięta poziomo do f(ax), pomnóż współrzędne x przez a.
- Zachowaj położenie punktów przecięcia y.
- Wynikowa funkcja będzie miała ten sam zakres, ale może mieć inną dziedzinę.
- Dany punkt (m, n), staje się (am, n), gdy rozciągnięty poziomo.
Zawsze wracajmy do tych pięciu wskazówek, gdy mamy wątpliwości. Umiejętność opanowania techniki poziomego rozciągania wykresów może nam pomóc w szybszym tworzeniu wykresów funkcji i zrozumieniu ich zachowania.
Czy jesteś gotowy, aby sprawdzić swoją wiedzę? Spróbujmy rozwiązać kilka z tych problemów!
Przykład 1
Funkcję g(x) otrzymujemy przez poziome rozciągnięcie wykresu f(x) = 8x o współczynnik skali 1/4. Które z poniższych wyrażeń jest poprawne dla g(x)?
a. g(x) = 32x
b. g(x) =16x
c. g(x) = 2x
d. g(x) =1/2 x
Rozwiązanie
Pamiętajmy, że gdy poziomo rozciągamy funkcję o 1/a, to dzielimy wartość wejściową przez a. Dlaczego nie zastosujemy tego do problemu? Zastąpimy x przez x/4, aby znaleźć wyrażenie dla g(x).
g(x) = 8(x/4)
Uproszczenie wyrażenia doprowadzi do tego, że g(x) = 2x.
Przykład 2
Zapisz wyrażenia dla g(x) i h(x) w postaci f(x), biorąc pod uwagę następujące warunki:
a. Funkcja g(x) jest wynikiem rozciągnięcia f(x) w poziomie o współczynnik 1/5.
b. Gdy poziomo rozciągniemy g(x) o współczynnik skali równy 1/2, otrzymamy h(x).
Rozwiązanie
Zacznijmy od g(x). Możemy poziomo rozciągnąć f(x), aby otrzymać g(x), więc podzielimy wartość wejściową f(x) przez 5, aby otrzymać wyrażenie g(x): f(x/5).
Gdy mamy już g(x), możemy znaleźć wyrażenie dla h(x). Dzielimy wartość wejściową g(x) przez 2. Stąd mamy:
h(x) = g(x/2)
= f(x/5 -1/2 )
= f(x/10)
To oznacza, że w terminach f(x), g(x) = f(x/5) i h(x)= f(x/10).
Przykład 3
Funkcja, f(x), przechodzi przez punkt (6, 4). Jeśli funkcja f(x) zostanie poziomo rozciągnięta o współczynnik skali 1/2, to jaka będzie nowa współrzędna x tego punktu?
Rozwiązanie
Gdy rozciągamy wykres poziomo, mnożymy współrzędną x funkcji bazowej przez dany mianownik współczynnika skali, aby znaleźć nowy punkt leżący wzdłuż tej samej współrzędnej y.
Stąd mamy (6, 4) → (2 ∙ 6, 4). Nową współrzędną x punktu będzie (12, 4).
Przykład 4
Tablica wartości dla f(x) jest pokazana poniżej. Jeśli h(x) jest wynikiem poziomego rozciągnięcia f(x) o współczynnik skali 1/4, skonstruuj jego tablicę wartości i zachowaj bieżące wartości wyjściowe.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
Rozwiązanie
Gdy funkcja jest rozciągnięta w poziomie, mnożymy wartości wejściowe (w tym przypadku są to wartości x) przez mianownik danego współczynnika skali.
To oznacza, że (-2, -4) zostanie przekształcone do (4∙ -2, -4) = (-8, -4). Zastosujemy ten sam proces dla pozostałych wartości i otrzymamy tablicę wartości h(x), jak pokazano poniżej.
| x | -12 | -8 | -.4 | 0 | 4 | 8 | 12 |
| h(x) | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
Przykład 5
Obserwuj funkcje przedstawione poniżej. Jaka jest zależność między f(x) i g(x)?
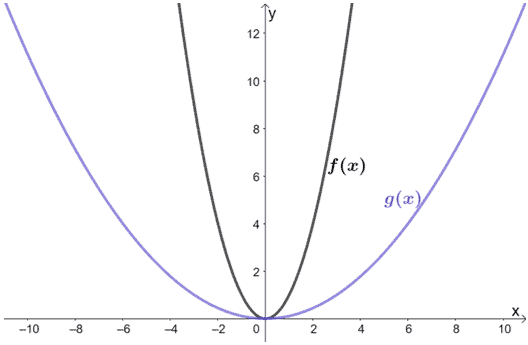
Rozwiązanie
Patrząc na wykres widzimy, że g(x) wynika z tego, że f(x) jest rozciągnięta poziomo. Dlaczego nie sprawdzimy kilku punktów z obu wykresów?
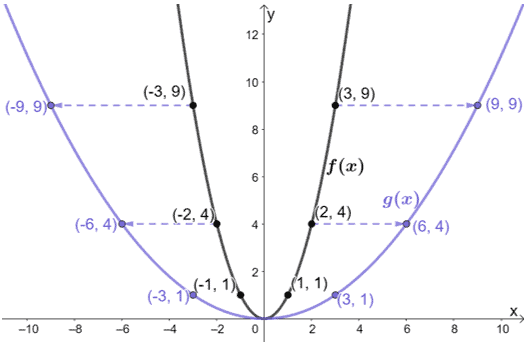
Oto, co dzieje się z punktami:
- (-3, 9) → (-9, 9)
- (-2, 4) → (-6, 4)
- (-1, 1) → (-3, 1)
- (0, 0) → (0, 0)
- (1, 1) → (3, 1)
- (2, 4) → (6, 4)
- (3, 9) → (9, 9)
Zauważ, jak dla każdego przypadku: współrzędne x dla g(x) są wszystkie trzy razy większe niż f(x). Oznacza to, że współczynnik skali użyty do rozciągnięcia f(x) jest równy 1/3.
Funkcja g(x) jest wynikiem poziomego rozciągnięcia f(x) o współczynnik skali równy 1/3.
Przykład 6
Następny obrazek przedstawia wykres f(x). Wykreśl wykres g(x) wykorzystując fakt, że jest on wynikiem poziomego rozciągnięcia f(x) o współczynnik 1/2. Upewnij się, że uwzględniłeś nowe punkty krytyczne dla g(x).
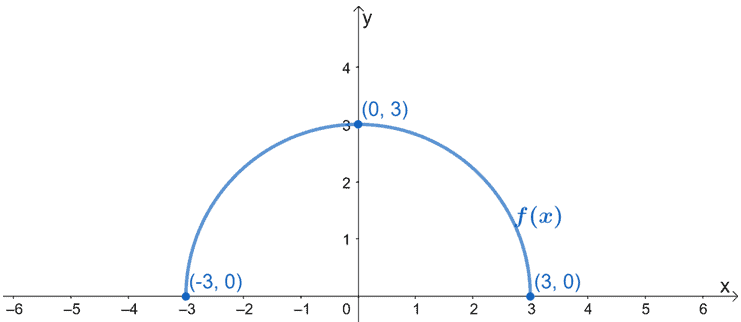
Rozwiązanie
Znajdźmy najpierw nowe punkty krytyczne dla g(x). Ponieważ f(x) będzie rozciągnięta poziomo, pomnożymy współrzędne x przez 2. W ten sposób otrzymamy następujące punkty krytyczne:
- (-3, 0) → (-6, 0)
- (0, 3) → (0, 3)
- (3, 0) → (6, 0)
Wyznacz te punkty i rozciągnij wykres f(x) o 3. Upewnij się, że współrzędne y i punkt przecięcia y pozostają takie same.
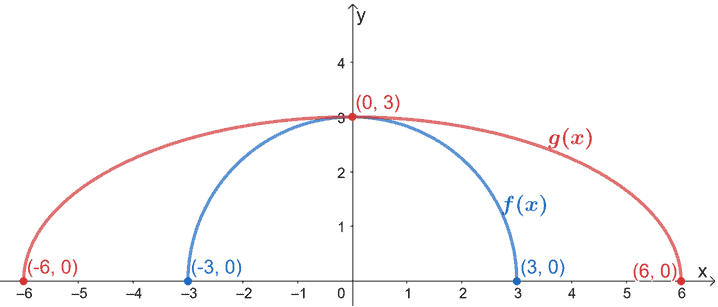
Tak powinien wyglądać wykres wynikowy. Ponieważ g(x) jest wynikiem rozciągnięcia f(x) w poziomie, to wykres f(x) rozciągamy o skalę 3.
Przykład 7
Opisać przekształcenia wykonane na następujących funkcjach przedstawionych poniżej.
a.f(x) = x2 → g(x) = x2/9
b. m(x) = √x → n(x) = 3√(x/4)
c. p(x) = 3x – 1→ q(x) = 3x/4 – 2
Rozwiązanie
Jeśli zauważyłeś, że niektóre z nich mogą wykazywać nie tylko poziome rozciągnięcia, to masz rację!
Pamiętaj, że czasami musimy zastosować różne techniki przekształceń, aby otrzymać wyrażenie danej funkcji.
Zacznijmy od f(x) i g(x):
Aby sprawdzić współczynnik skali zastosowany w wartości wejściowej f(x) w celu uzyskania g(x), wyraźmy g(x) jako doskonały kwadrat: g(x) = (x/3)2 = (1/3 – x)2.
Wyrażając g(x) w kategoriach f(x), mamy g(x) = f(x/3). Stąd, g(x) jest wynikiem poziomego rozciągnięcia f(x) o współczynnik skali 1/3.
Przechodząc do m(x) i n(x):
Widzimy dwa współczynniki skali zastosowane do n(x): 3 dla wartości wyjściowej i 1/4 dla wartości wejściowej. Stosując to, co wiemy o rozciągnięciach pionowych i poziomych, mamy n(x) = 3-m(1/4 – x). Oznacza to, że n(x) jest wynikiem rozciągnięcia m(x) w pionie o współczynnik skali 3 i w poziomie o współczynnik skali 1/4.
Na koniec zaobserwujmy translacje wykonane na p(x).
q(x) = 3/4 x – 1 – 1
= 3(x/4) – 1 – 1
= p(x/4) – 1
Wynika z tego, że q(x) jest wynikiem rozciągnięcia p(x) w poziomie o współczynnik skali 1/4 i przesunięcia o jedną jednostkę w dół.
Przykład 8
Jakie przekształcenia wykonujemy na f(x), aby w wyniku tego otrzymać g(x) = 2|x/3| – 1? Skorzystaj z wykresu f(x) przedstawionego poniżej. Zastosuj przekształcenia do wykresu g(x).
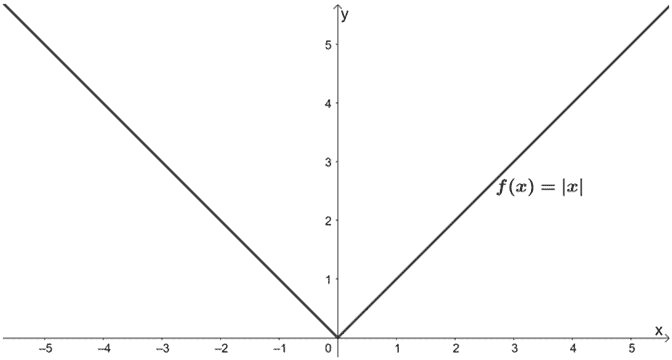
Rozwiązanie
Przejdźmy dalej i wyraźmy g(x) w kategoriach f(x).
g(x) = 2 – |1/3 – x| – 1
= 2- f(x/3) – 1
To oznacza, że przesunięcia na f(x) w celu otrzymania g(x) są następujące:
- Poziomo rozciągnięte o współczynnik skali 1/3.
- Pionowo rozciągnięta o współczynnik skali 2.
- Przesunięta w dół o 1 jednostkę.
Powoli zastosujmy te przekształcenia na f(x), zaczynając od poziomego rozciągnięcia f(x).
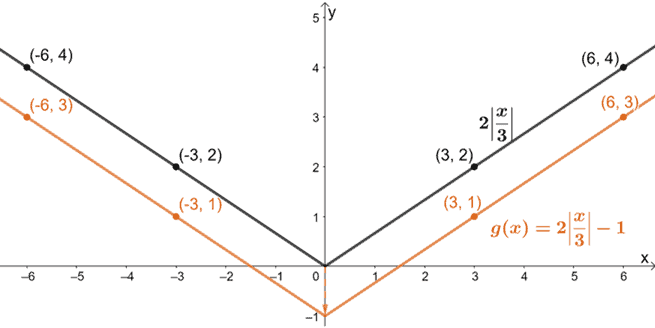
Rozciągnijmy teraz otrzymany wykres w pionie o współczynnik skali 2.
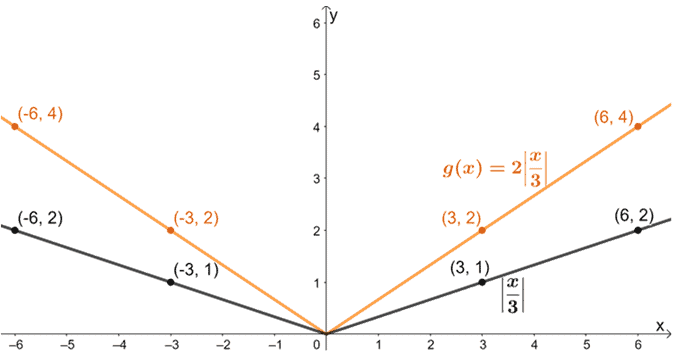
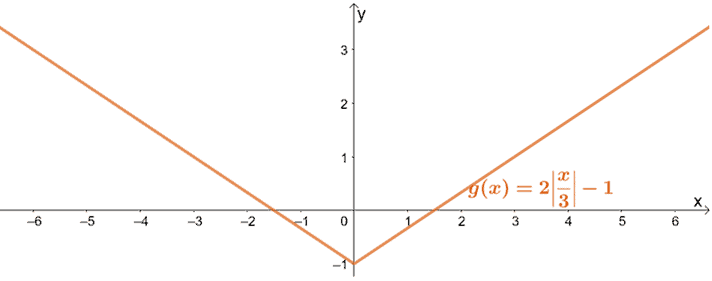
Na koniec przetłumaczmy wykres o jedną jednostkę w dół.
Więc właśnie pokazaliśmy, jak można przedstawić wykres g(x) za pomocą funkcji macierzystej funkcji wartości bezwzględnej, f(x) = |x|.
Pytania praktyczne
1. Funkcję g(x) otrzymujemy przez poziome rozciągnięcie f(x) = 16×2 o współczynnik skali 2. Które z poniższych wyrażeń jest poprawnym wyrażeniem dla g(x)?
a. g(x) = 32×2
b. g(x) = 16×2
c. g(x) = 8×2
d. g(x) = 2×2
2. Napisz wyrażenia dla g(x) i h(x) w postaci f(x), jeśli spełnione są następujące warunki:
a. Funkcja g(x) jest wynikiem poziomego rozciągnięcia f(x) o współczynnik 1/4.
b. Gdy poziomo rozciągniemy g(x) o współczynnik skali 1/3, otrzymamy h(x).
3. Funkcja, f(x), przechodzi przez punkt (10, 8). Jeśli funkcja f(x) zostanie rozciągnięta w poziomie o współczynnik skali 5, to jaka będzie nowa współrzędna x tego punktu?
4. Tablica wartości funkcji f(x) jest pokazana poniżej. Jeśli g(x) jest wynikiem poziomego rozciągnięcia f(x) o współczynnik skali 3, to skonstruuj jego tablicę wartości i zachowaj bieżące wartości wyjściowe.
| x | -9 | -6 | -3 | 0 | 3 | 6 | 9 |
| f(x) | -17 | -11 | -5 | 1 | 7 | 13 | 19 |
5. Zaobserwuj funkcje przedstawione poniżej. Jaki jest związek między f(x) i g(x)?
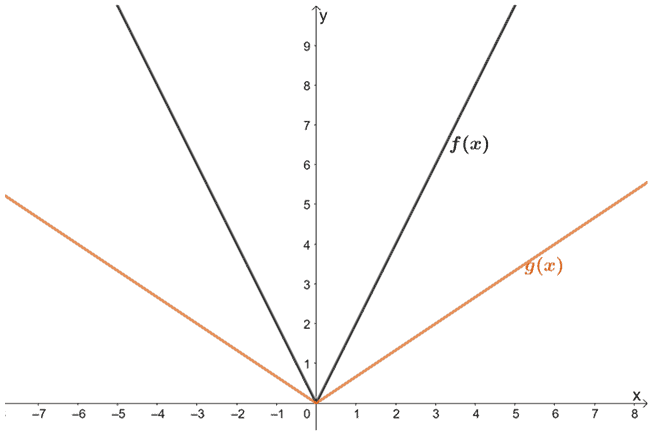
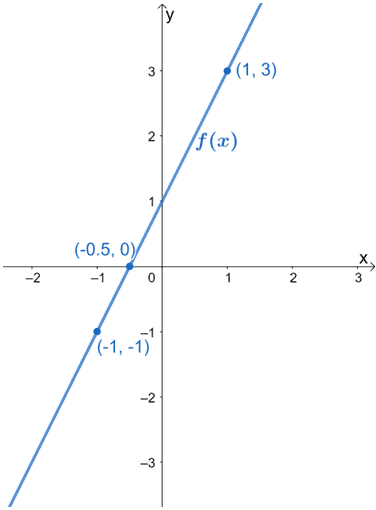
6. Poniższy rysunek przedstawia wykres f(x). Wykreśl wykres h(x) korzystając z faktu, że jest on wynikiem rozciągnięcia f(x) w poziomie o współczynnik 1/3. Pamiętaj, aby uwzględnić nowe punkty krytyczne dla g(x).
7. Opisz przekształcenia dokonane na następujących funkcjach przedstawionych poniżej.
a. f(x) = x2 → g(x) = x2/16
b. m(x) = √x → n(x) = √(x/5) + 3
c. p(x) = 2x + 1→ q(x) = 2x/3 + 2
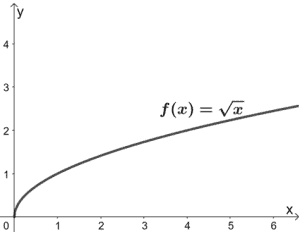
8. Jakie przekształcenia wykonano na funkcji f(x), aby jej wynikiem było g(x) = 3√(x/2)? Skorzystaj z wykresu f(x) przedstawionego poniżej. Zastosuj przekształcenia do wykresu g(x).
Obrazy/rysunki matematyczne tworzone są za pomocą programu GeoGebra.
Wykonaj rysunek za pomocą programu GeoGebra.