Wybór najlepszego algorytmu uczenia maszynowego dla problemu regresji

Ostatnio rozpocząłem wydawanie biuletynu edukacyjnego o tematyce książkowej.skupiony na książkach newsletter edukacyjny. Book Dives to dwutygodnik, w którym w każdym nowym numerze zagłębiamy się w książkę non-fiction. Dowiesz się, jakie są jej główne lekcje i jak je zastosować w życiu. Możesz zapisać się na niego tutaj.

Podchodząc do każdego rodzaju problemu związanego z uczeniem maszynowym (ML) istnieje wiele różnych algorytmów do wyboru. W uczeniu maszynowym istnieje coś, co nazywa się twierdzeniem „No Free Lunch”, które zasadniczo stwierdza, że żaden jeden algorytm ML nie jest najlepszy dla wszystkich problemów. Wydajność różnych algorytmów ML silnie zależy od rozmiaru i struktury danych. W związku z tym, właściwy wybór algorytmu często pozostaje niejasny, chyba że przetestujemy nasze algorytmy bezpośrednio poprzez zwykłe stare próby i błędy.

Ale istnieją pewne zalety i wady każdego algorytmu ML, które możemy wykorzystać jako wskazówki. Chociaż jeden algorytm nie zawsze będzie lepszy od drugiego, istnieją pewne właściwości każdego algorytmu, które możemy wykorzystać jako wskazówkę przy szybkim wyborze właściwego i dostrajaniu parametrów. Zamierzamy przyjrzeć się kilku wybitnym algorytmom ML dla problemów regresji i ustalić wytyczne, kiedy ich używać w oparciu o ich mocne i słabe strony. Ten post powinien służyć jako pomoc w wyborze najlepszego algorytmu ML dla Twojego problemu regresji!

Zanim zaczniemy, sprawdź biuletyn AI Smart, aby przeczytać najnowsze i najlepsze informacje na temat AI, uczenia maszynowego i nauki o danych!

Regresja liniowa i wielomianowa

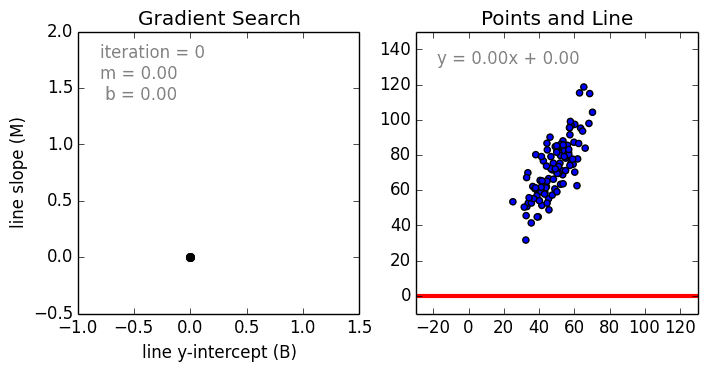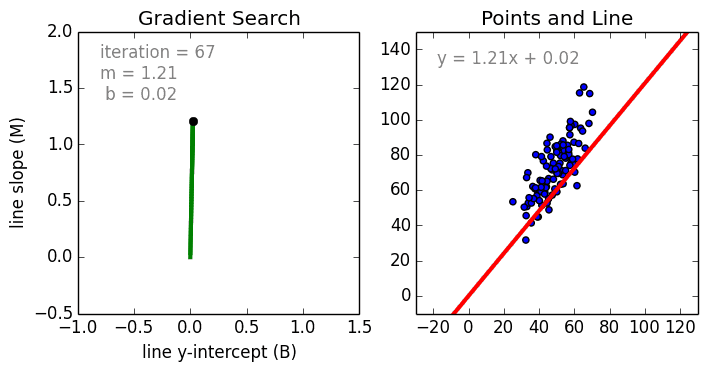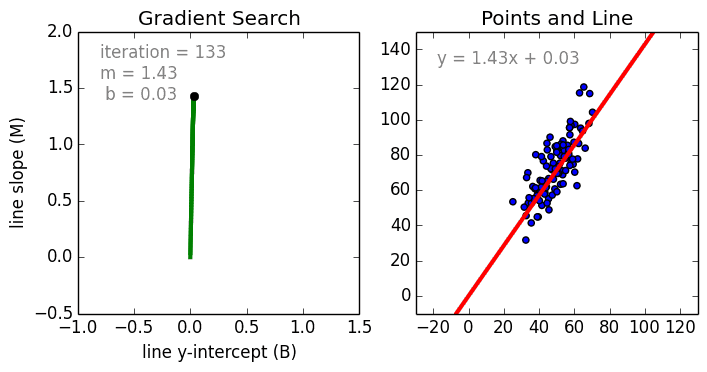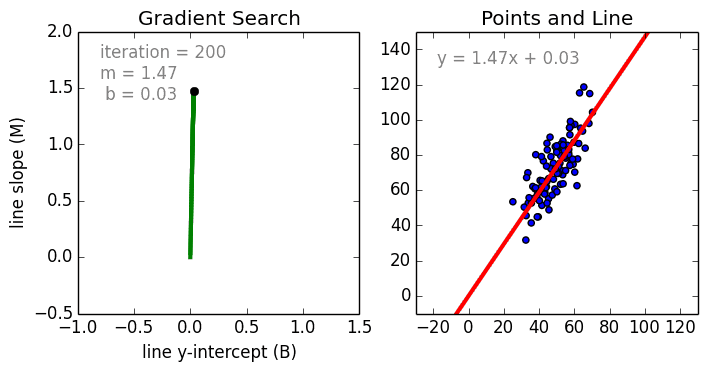
Zacznijmy od prostego przypadku, Regresja liniowa jednowariantowa jest techniką używaną do modelowania zależności pomiędzy pojedynczą wejściową zmienną niezależną (zmienną cechową) a wyjściową zmienną zależną za pomocą modelu liniowego i.tj. linii. Bardziej ogólnym przypadkiem jest Regresja Liniowa Wielozmienna, gdzie model jest tworzony dla relacji pomiędzy wieloma niezależnymi zmiennymi wejściowymi (zmienne cechy) i zmienną zależną na wyjściu. Model pozostaje liniowy w tym, że wyjście jest liniową kombinacją zmiennych wejściowych.

Jest trzeci najbardziej ogólny przypadek zwany Regresją wielomianową, gdzie model staje się nieliniową kombinacją zmiennych cech tj. mogą być zmienne wykładnicze, sinusoidalne i kosinusoidalne, itp. Wymaga to jednak wiedzy o tym, jak dane odnoszą się do danych wyjściowych. Modele regresji mogą być szkolone przy użyciu Stochastic Gradient Descent (SGD).

Pros:

• Szybki do modelowania i jest szczególnie przydatny, gdy relacja do modelowania nie jest bardzo złożona i jeśli nie masz dużo danych.
• Regresja liniowa jest prosta do zrozumienia, co może być bardzo cenne przy podejmowaniu decyzji biznesowych.

Konkursy:

• Dla danych nieliniowych regresja wielomianowa może być dość trudna do zaprojektowania, ponieważ trzeba mieć pewne informacje o strukturze danych i relacjach między zmiennymi funkcji.
• W wyniku powyższego, modele te nie są tak dobre jak inne, jeśli chodzi o bardzo złożone dane.

Sieci neuronowe

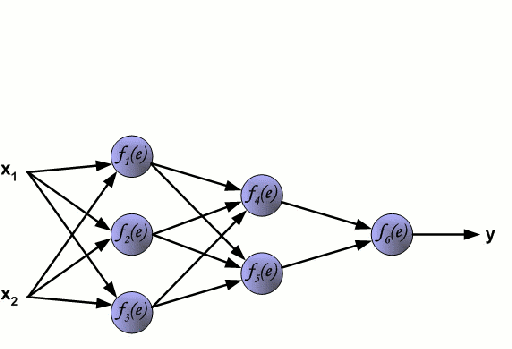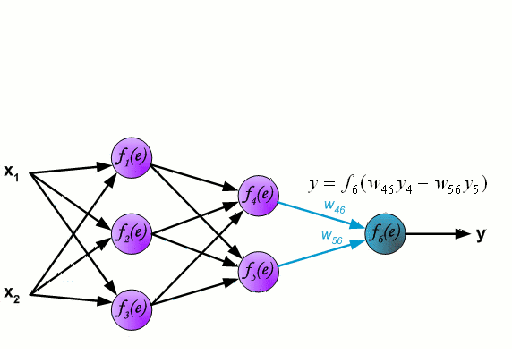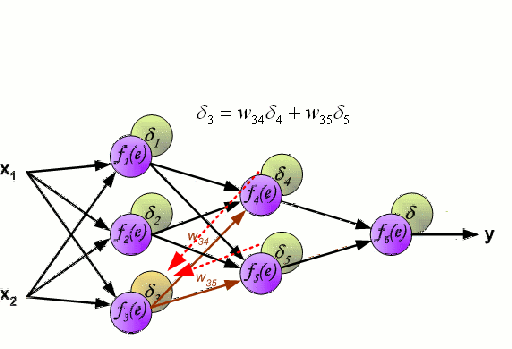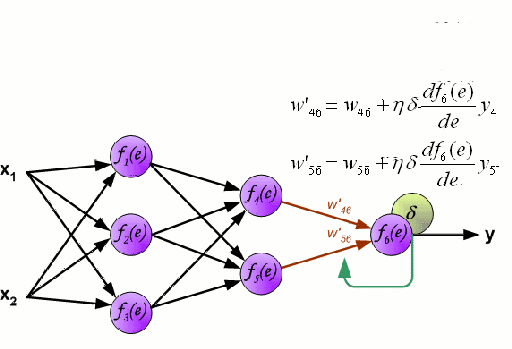
Sieć neuronowa składa się z wzajemnie połączonej grupy węzłów zwanych neuronami. Wejściowe zmienne cech z danych są przekazywane do tych neuronów jako wielozmienna kombinacja liniowa, gdzie wartości pomnożone przez każdą zmienną cech są znane jako wagi. Nieliniowość jest następnie stosowana do tej kombinacji liniowej, co daje sieci neuronowej zdolność do modelowania złożonych zależności nieliniowych. Sieć neuronowa może mieć wiele warstw, gdzie wyjście z jednej warstwy jest przekazywane do następnej w ten sam sposób. Na wyjściu na ogół nie ma zastosowanej nieliniowości. Sieci neuronowe są szkolone przy użyciu Stochastic Gradient Descent (SGD) i algorytmu wstecznej propagacji (oba wyświetlane w GIF powyżej).

Pros:

• Ponieważ sieci neuronowe mogą mieć wiele warstw (a więc i parametrów) z nieliniowością, są bardzo skuteczne w modelowaniu bardzo złożonych relacji nieliniowych.
• Na ogół nie musimy się martwić o strukturę danych, ponieważ sieci neuronowe są bardzo elastyczne w uczeniu się prawie każdego rodzaju zmiennych funkcji.
• Badania konsekwentnie wykazują, że po prostu dając sieci więcej danych treningowych, czy to zupełnie nowych, czy z rozszerzenia oryginalnego zestawu danych, korzystnie wpływa na wydajność sieci.

Konsekwencje:

• Z powodu złożoności tych modeli, nie są one łatwe do interpretacji i zrozumienia.
• Mogą być dość trudne i intensywne obliczeniowo do wytrenowania, wymagając starannego dostrojenia hiper-parametrów i ustawienia harmonogramu szybkości uczenia.
• Wymagają dużej ilości danych, aby osiągnąć wysoką wydajność i są generalnie gorsze od innych algorytmów ML w przypadkach „małych danych”.

Drzewa regresyjne i lasy losowe

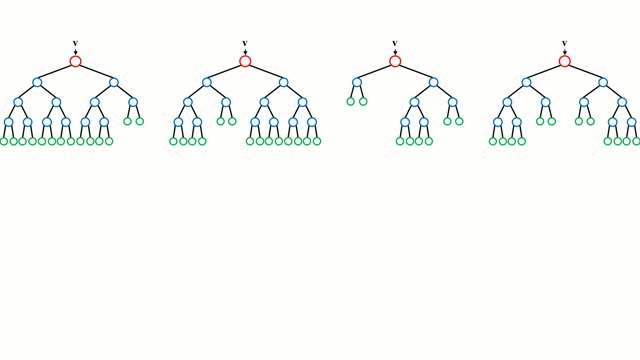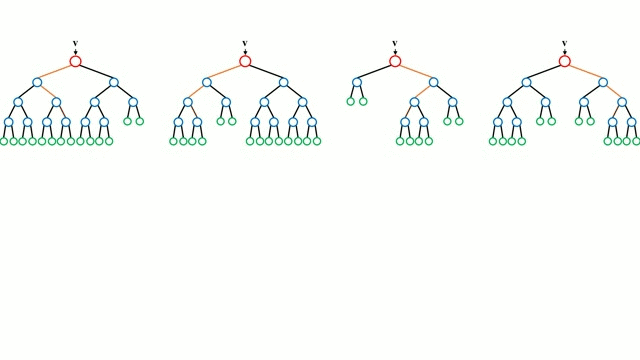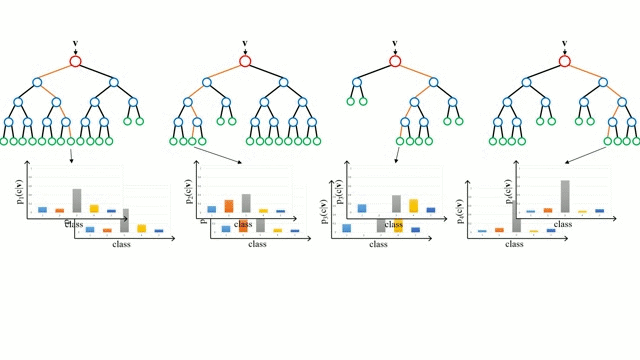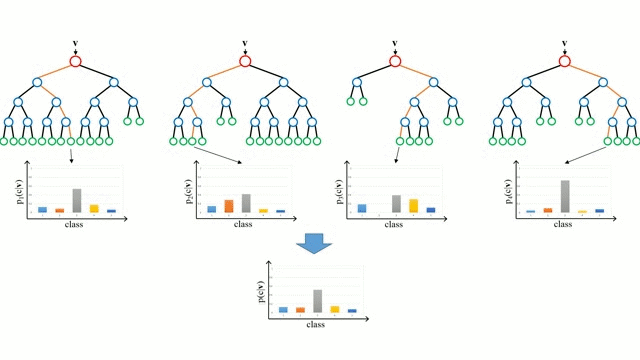
Zaczynając od przypadku bazowego, Drzewo decyzyjne jest intuicyjnym modelem, w którym przechodzimy przez kolejne gałęzie drzewa i wybieramy następną gałąź na podstawie decyzji podjętej w węźle. Indukcja drzewa jest zadaniem polegającym na przyjęciu zbioru instancji szkoleniowych jako danych wejściowych, podjęciu decyzji, które atrybuty są najlepsze do podziału, podzieleniu zbioru danych i powtarzaniu na wynikowych podzielonych zbiorach danych, aż wszystkie instancje szkoleniowe zostaną skategoryzowane. Podczas budowania drzewa, celem jest podział na atrybuty, które tworzą najczystsze węzły potomne, co ograniczy do minimum liczbę podziałów, które musiałyby być wykonane, aby sklasyfikować wszystkie instancje w naszym zbiorze danych. Czystość jest mierzona przez pojęcie przyrostu informacji, które odnosi się do tego, jak wiele trzeba by wiedzieć o wcześniej niewidzianej instancji, aby została ona poprawnie sklasyfikowana. W praktyce jest to mierzone poprzez porównanie entropii, czyli ilości informacji potrzebnych do sklasyfikowania pojedynczej instancji w aktualnej partycji zbioru danych, do ilości informacji potrzebnych do sklasyfikowania pojedynczej instancji, gdyby aktualna partycja zbioru danych została podzielona na kolejne partycje pod względem danego atrybutu.

Lasy losowe są po prostu zespołem drzew decyzyjnych. Wektor wejściowy jest przepuszczany przez wiele drzew decyzyjnych. W przypadku regresji, wartość wyjściowa wszystkich drzew jest uśredniana; w przypadku klasyfikacji, schemat głosowania jest używany do określenia ostatecznej klasy.

Pros:

• Doskonałe w uczeniu się złożonych, wysoce nieliniowych zależności. Zwykle mogą osiągnąć całkiem wysoką wydajność, lepszą niż regresja wielomianowa i często na równi z sieciami neuronowymi.
• Bardzo łatwe do interpretacji i zrozumienia. Chociaż ostateczny model może uczyć się złożonych zależności, granice decyzyjne, które są budowane podczas szkolenia są łatwe i praktyczne do zrozumienia.

Konsekwencje:

• Z powodu natury szkolenia drzew decyzyjnych mogą być podatne na poważne przepasowanie. Ukończony model drzewa decyzyjnego może być zbyt skomplikowany i zawierać niepotrzebną strukturę. Chociaż to może być czasami złagodzone przy użyciu odpowiedniego przycinania drzew i większych zespołów lasów losowych.
• Używanie większych zespołów lasów losowych w celu osiągnięcia wyższej wydajności wiąże się z wadami bycia wolniejszym i wymagającym więcej pamięci.

Wniosek

Boom! Oto twoje plusy i minusy! W następnym poście przyjrzymy się wadom i zaletom różnych modeli klasyfikacyjnych. Mam nadzieję, że podobał Ci się ten post i nauczyłeś się czegoś nowego i przydatnego. Jeśli tak, nie krępuj się i daj mu kilka klapsów.