Zastosowania wzmacniacza operacyjnego

Pierwszym przykładem jest wzmacniacz różnicowy, z którego można wyprowadzić wiele innych zastosowań, w tym wzmacniacz odwracający, nieodwracający, sumujący, wtórnik napięciowy, integrator, różniczkujący i żyrator.

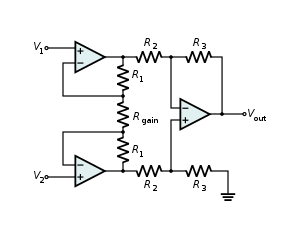
Wzmacniacz różnicowy (difference amplifier)Edycja

Główny artykuł: Wzmacniacz różnicowy

Wzmacnia różnicę napięć pomiędzy swoimi wejściami.

Nazwy „wzmacniacz różnicowy” nie należy mylić z „różnicówką”, która również jest przedstawiona na tej stronie. Wzmacniacz instrumentacyjny”, który również jest pokazany na tej stronie, jest modyfikacją wzmacniacza różnicowego, która również zapewnia wysoką impedancję wejściową.

Przedstawiony obwód oblicza różnicę dwóch napięć, pomnożoną przez pewien współczynnik wzmocnienia. Napięcie wyjściowe

V out = ( R f + R 1 ) R g ( R g + R 2 ) R 1 V 2 – R f R 1 V 1 = ( R 1 + R f R 1 ) ⋅ ( R g R g + R 2 ) V 2 – R f R 1 V 1 . {\displaystyle V_{\text{out}}={\frac {\left(R_{\text{f}}+R_{1}\right)R_{\text{g}}}{\left(R_{\text{g}}+R_{2}\right)R_{1}}}V_{2}-{\frac {R_{\text{f}}}{R_{1}}}V_{1}=\left({\frac {R_{1}+R_{\text{f}}}{R_{1}}}\right)\cdot \left({\frac {R_{\text{g}}}{R_{\text{g}}+R_{2}}}\right)V_{2}-{\frac {R_{\text{f}}}{R_{1}}}V_{1}.}

$V_{\text{out}}={\frac {\left(R_{\text{f}}+R_{1}\right)R_{\text{g}}}{\left(R_{\text{g}}+R_{2}\right)R_{1}}}V_{2}-{\frac {R_{\text{f}}}{R_{1}}}V_{1}=\left({\frac {R_{1}+R_{\text{f}}}{R_{1}}}\right)\cdot \left({\frac {R_{\text{g}}}{R_{\text{g}}+R_{2}}}\right)V_{2}-{\frac {R_{\text{f}}}{R_{1}}}V_{1}.$

Albo, wyrażone jako funkcja wejścia wspólnego trybu Vcom i wejścia różnicowego Vdif:

V com = ( V 1 + V 2 )/2 ; V dif = V 2 – V 1 , {{{text{com}}=(V_{1}+V_{2})/2;V_{\text{dif}}=V_{2}-V_{1},}

$V_{\text{com}}=(V_{1}+V_{2})/2;V_{text{dif}}=V_{2}-V_{1},$

napięcie wyjściowe wynosi

V out R 1 R f = V com R 1 / R f – R 2 / R g 1 + R 2 / R g + V dif 1 + ( R 2 / R g + R 1 / R f ) / 2 1 + R 2 / R g . {\displaystyle V_{\text{out}}{\frac {R_{1}}{R_{\text{f}}}}=V_{\text{com}}{\frac {R_{1}/R_{\text{f}}-R_{2}/R_{\text{g}}}{1+R_{2}/R_{\text{g}}}}+V_{\text{dif}}{\frac {1+(R_{2}/R_{\text{g}}+R_{1}/R_{\text{f}})/2}{1+R_{2}/R_{\text{g}}}}.}

$V_{\text{out}}{\frac {R_{1}}{R_{\text{f}}}}=V_{\text{com}}{\frac {R_{1}/R_{\text{f}}-R_{2}/R_{\text{g}}}{1+R_{2}/R_{\text{g}}}}+V_{\text{dif}}{\frac {1+(R_{2}/R_{\text{g}}+R_{1}/R_{\text{f}})/2}{1+R_{2}/R_{\text{g}}}}.$

Aby układ ten wytwarzał sygnał proporcjonalny do różnicy napięć na zaciskach wejściowych, współczynnik składowej Vcom (wzmocnienie trybu wspólnego) musi być równy zero, czyli

R 1 / R f = R 2 / R g . {displaystyle R_{1}/R_{text{f}}=R_{2}/R_{text{g}}.}

$R_{1}/R_{\text{f}}=R_{2}/R_{\text{g}}.$

Dzięki temu ograniczeniu współczynnik odrzucania fazy wspólnej w tym obwodzie jest nieskończenie duży, a wyjście

V out = R f R 1 V dif = R f R 1 ( V 2 – V 1 ) , {\displaystyle V_{\text{out}}={\frac {R_{\text{f}}}{R_{1}}}V_{\text{dif}}={\frac {R_{\text{f}}}{R_{1}}}\left(V_{2}-V_{1}\right),}

$V_{\text{out}}={\frac {R_{\text{f}}}{R_{1}}}V_{\text{dif}}={\frac {R_{\text{f}}}{R_{1}}}\left(V_{2}-V_{1}\right),$

gdzie proste wyrażenie Rf / R1 reprezentuje wzmocnienie wzmacniacza różnicowego w pętli zamkniętej.

Specjalnym przypadkiem, gdy wzmocnienie pętli zamkniętej jest równe jedności, jest wtórnik różnicowy, gdzie

V out = V 2 – V 1 . {\displaystyle V_{\text{out}}=V_{2}-V_{1}.}

${displaystyle V_{text{out}}=V_{2}-V_{1}.}$

Wzmacniacz odwracającyEdit

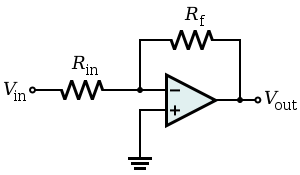
Wzmacniacz odwracający jest szczególnym przypadkiem wzmacniacza różnicowego, w którym nieodwracające wejście V2 jest uziemione, a wejście odwracające V1 jest utożsamiane z Vin powyżej. Wzmocnienie w pętli zamkniętej wynosi Rf / Rin, stąd

V out = – R f R in V in {{displaystyle V_{text{out}}=-{frac {R_{text{f}}}{R_{text{in}}}}V_{text{in}}}}.\,}

$V_{{{\text{out}}}}=-{\frac {R_{{{\text{f}}}}}{R_{{{\text{in}}}}}}V_{{{\text{in}}}}\!\,$

Powyższy uproszczony układ przypomina wzmacniacz różnicowy w granicy bardzo małych wartości R2 i Rg. W tym przypadku jednak, układ będzie podatny na dryft wejściowego prądu biasu z powodu niedopasowania Rf i Rin.

Aby intuicyjnie zobaczyć powyższe równanie wzmocnienia, oblicz prąd w Rin:

i in = V w R w {{displaystyle i_{text{in}}={{frac {V_{text{in}}}{R_{text{in}}}}}

$i_{{text{in}}}}={{}frac {V_{{text{in}}}}}{R_{{}text{in}}}}}}$

przypomnijmy, że ten sam prąd musi przepływać przez Rf, zatem (ponieważ V- = V+ = 0):

V out = – i w R f = – V w R f R w {{displaystyle V_{text{out}}=-i_{text{in}}R_{text{f}}=-V_{text{in}}}{{frac {R_{text{f}}}}{R_{text{in}}}}}

$V_{text{out}} = -i_{text{in}} R_{text{f}} = - V_{text{in}} \_frac{ R_{text{f}} }{ R_{text{in}} }$

Mechaniczną analogią jest huśtawka, z węzłem V- (pomiędzy Rin i Rf) jako punktem podparcia, przy potencjale masy. Vin znajduje się na długości Rin od punktu podparcia; Vout jest na długości Rf. Kiedy Vin schodzi „poniżej ziemi”, wyjściowy Vout rośnie proporcjonalnie, aby zrównoważyć huśtawkę, i odwrotnie.

Jako że ujemne wejście op-ampa działa jak wirtualna ziemia, impedancja wejściowa tego obwodu jest równa Rin.

Wzmacniacz nieodwracającyEdit

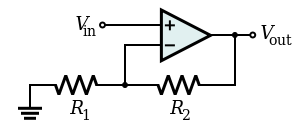
Wzmacniacz nieodwracający jest specjalnym przypadkiem wzmacniacza różnicowego, w którym wejście odwracające V1 jest uziemione, a wejście nieodwracające V2 jest utożsamiane z Vin powyżej, z R1 ≫ R2.Odnosząc się do obwodu bezpośrednio powyżej,

V out = ( 1 + R 2 R 1 ) V in {displaystyle V_{text{out}}=left(1+{frac {R_{text{2}}}}{R_{text{1}}}}}}}right)V_{text{in}}}}.\,}

$V_{{{\text{out}}}}=\left(1+{\frac {R_{{{\text{2}}}}}{R_{{{\text{1}}}}}}\right)V_{{{\text{in}}}}\!\,$

Aby intuicyjnie zobaczyć to równanie wzmocnienia, użyj techniki wirtualnej ziemi, aby obliczyć prąd w rezystorze R1:

i 1 = V w R 1 , {{displaystyle i_{1}={{frac {V_{w}}}}}{R_{1}}}},}

$i_{1}={{frac {V_{w}}}}}{R_{1}}},$

przypomnijmy, że ten sam prąd musi przepływać przez R2, zatem:

V out = V in + i 1 R 2 = V in ( 1 + R 2 R 1 ) {{{displaystyle V_{text{out}}=V_{text{in}}+i_{1}R_{2}=V_{text{in}}}lewa(1+{frac {R_{2}}{R_{1}}}prawa)}

${displaystyle V_{text{out}}=V_{text{in}}+i_{1}R_{2}=V_{text{in}}}left(1+{frac {R_{2}}{R_{1}}}}right)}$

W przeciwieństwie do wzmacniacza odwracającego, wzmacniacz nieodwracający nie może mieć wzmocnienia mniejszego niż 1.

Mechaniczną analogią jest dźwignia klasy 2, z jednym zaciskiem R1 jako punktem podparcia, przy potencjale masy. Vin jest na długości R1 od punktu podparcia; Vout jest na długości R2 dalej. Gdy Vin wznosi się „nad ziemię”, wyjściowe Vout rośnie proporcjonalnie do dźwigni.

Impedancja wejściowa uproszczonego wzmacniacza nieodwracającego jest wysoka:

Z in = ( 1 + A OL B ) Z dif {{displaystyle Z_{text{in}}=(1+A_{text{OL}}B)Z_{text{dif}}}

${{displaystyle Z_{text{in}}=(1+A_{text{OL}}B)Z_{text{dif}}}$

gdzie Zdif jest impedancją wejściową op-ampa dla sygnałów różnicowych, i AOL jest wzmocnieniem napięciowym op-ampa w otwartej pętli (które zmienia się z częstotliwością), a B jest współczynnikiem sprzężenia zwrotnego (ułamek sygnału wyjściowego, który wraca na wejście). W przypadku idealnego op-ampa, z AOL nieskończonym i Zdif nieskończonym, impedancja wejściowa jest również nieskończona. W tym przypadku jednak, układ będzie podatny na dryft wejściowego prądu biasu z powodu niedopasowania impedancji napędzających wejścia V+ i V- opampa.

Pętla sprzężenia zwrotnego podobnie zmniejsza impedancję wyjściową:

Z out = Z OL 1 + A OL B {{displaystyle Z_{text{out}}={{{frac {Z_{text{OL}}}}{1+A_{text{OL}}}B}}}}.

${displaystyle Z_{text{out}}={frac {Z_{text{OL}}}{1+A_{text{OL}}}B}}}$

gdzie Zout jest impedancją wyjściową ze sprzężeniem zwrotnym, a ZOL jest impedancją wyjściową w otwartej pętli.

Wzmacniacz podążający za napięciem (wzmacniacz buforowy unity)Edycja

Używany jako wzmacniacz buforowy w celu wyeliminowania efektów obciążenia (np, podłączenie urządzenia o wysokiej impedancji źródłowej do urządzenia o niskiej impedancji wejściowej).

V out = V in {{displaystyle V_{text{out}}=V_{text{in}}}}.

${{displaystyle V_{text{out}}=V_{text{in}}}$

Z in = ∞ {{displaystyle Z_{text{in}}={infty }

$Z_{{text{in}}}}=}}$

(realistycznie, różnicowa impedancja wejściowa samego op-ampa (1 MΩ do 1 TΩ), pomnożona przez wzmocnienie op-ampa w otwartej pętli)

Z powodu silnego (tj. jedności wzmocnienia) sprzężenia zwrotnego i pewnych nieidealnych właściwości rzeczywistych wzmacniaczy operacyjnych, ten układ sprzężenia zwrotnego jest podatny na posiadanie słabych marginesów stabilności. W konsekwencji, układ może być niestabilny, gdy jest podłączony do obciążeń o wystarczającej pojemności. W takich przypadkach, aby przywrócić stabilność, można zastosować sieć kompensacji opóźnienia (np. łącząc obciążenie z wtórnikiem napięciowym przez rezystor). Karta katalogowa producenta wzmacniacza operacyjnego może zawierać wskazówki dotyczące doboru elementów w zewnętrznych sieciach kompensacyjnych. Alternatywnie można wybrać inny wzmacniacz operacyjny, który ma bardziej odpowiednią kompensację wewnętrzną.

Na impedancję wejściową i wyjściową wpływa pętla sprzężenia zwrotnego w taki sam sposób, jak w przypadku wzmacniacza nieodwracającego, przy B=1.

Wzmacniacz sumującyEdit

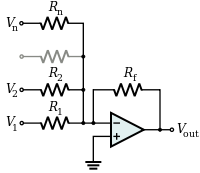
Wzmacniacz sumujący sumuje kilka (ważonych) napięć:

V out = – R f ( V 1 R 1 + V 2 R 2 + ⋯ + V n R n ) {{displaystyle V_{text{out}}=-.R_{text{f}}left({ {{frac {V_{1}}{R_{1}}}+{{frac {V_{2}}{R_{2}}}}+}cdots +{{frac {V_{n}}{R_{n}}}}right)}

$V_{{text{out}}}}=-.R_{{text{f}}}}}}left({{{frac {V_{1}}{R_{1}}}+{{{frac {V_{2}}{R_{2}}}}+}cdots +{{frac {V_{n}}{R_{n}}}}right)$

Gdy R 1 = R 2 = ⋯ = R n {{displaystyle R_{1}=R_{2}=cdots =R_{n}}}
$R_{1}=R_{2}=R_{n}$

, a R f {{displaystyle R_{text{f}}}

$R_{{text{f}}}}$

niezależne

V out = – R f R 1 ( V 1 + V 2 + ⋯ + V n ) {displaystyle V_{text{out}}=-.{{frac {R_{text{f}}}{R_{1}}}(V_{1}+V_{2}+cdots +V_{n})}}.}

${displaystyle V_{text{out}}=-{}frac {R_{text{f}}}{R_{1}}}(V_{1}+V_{2}+cdots +V_{n})}}.}$

Gdy R 1 = R 2 = ⋯ = R n = R f {{displaystyle R_{1}=R_{2}= R_{dots =R_{n}=R_{text{f}}}
$R_{1}=R_{2}=cdots =R_{n}=R_{text{f}}}}$

V out = – ( V 1 + V 2 + ⋯ + V n ) {displaystyle V_{text{out}}=-(V_{1}+V_{2}+cdots +V_{n}})}

${displaystyle V_{text{out}}=-(V_{1}+V_{2}+przyciski +V_{n})}$

Wyjście jest odwrócone
Impedancja wejściowa n-tego wejścia wynosi Z n = R n {{displaystyle Z_{n}=R_{n}}
$Z_{n}=R_{n}$

( V – {displaystyle V_{-}}

$V_{-}$

jest wirtualną masą)