Álgebra Universitária
Resultados de aprendizagem
- Converter de forma logarítmica para forma exponencial.
- Converter de forma exponencial para forma logarítmica.
A fim de analisar a magnitude dos terramotos ou comparar as magnitudes de dois terramotos diferentes, precisamos de ser capazes de converter entre a forma logarítmica e exponencial. Por exemplo, suponha que a quantidade de energia libertada por um terramoto foi 500 vezes maior do que a quantidade de energia libertada por outro. Queremos calcular a diferença de magnitude. A equação que representa este problema é {10}^{x}=500 onde x representa a diferença de magnitudes na Escala Richter. Como resolveríamos para x?
p> Ainda não aprendemos um método de resolução algébrica de equações exponenciais. Nenhuma das ferramentas algébricas discutidas até agora é suficiente para resolver {10}^{x}=500. Sabemos que {10}^{2}=100 e {10}^{3}=1000, pelo que é evidente que x deve ter algum valor entre 2 e 3, uma vez que y={10}^{x} está a aumentar. Podemos examinar um gráfico para melhor estimar a solução.
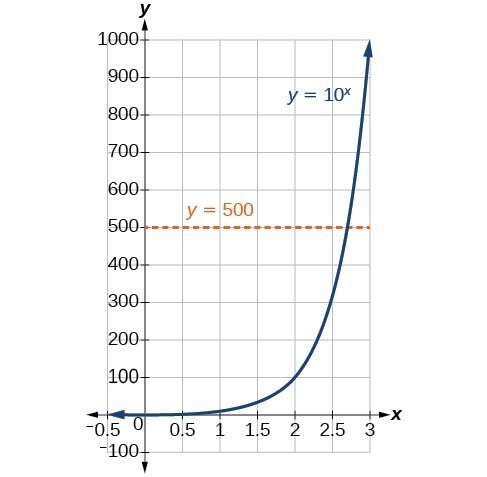
Estimando a partir de um gráfico, no entanto, é impreciso. Para encontrar uma solução algébrica, temos de introduzir uma nova função. Observar que o gráfico acima passa no teste da linha horizontal. A função exponencial y={b}^{x} é um-para-um, pelo que o seu inverso, x={b}^{y} é também uma função. Como é o caso de todas as funções inversas, simplesmente trocamos x e y e resolvemos por y para encontrar a função inversa. Para representar y como uma função de x, utilizamos uma função logarítmica da forma y={\mathrm{log}}_{b}{esquerda(x) direita}. O logaritmo base b de um número é o expoente pelo qual devemos elevar b para obter esse número.
Lemos uma expressão logarítmica como, “O logaritmo com base b de x é igual a y”, ou, simplificado, “logaritmo base b de x é y”. Podemos também dizer, “b elevado ao poder de y é x”, porque os logaritmos são expoentes. Por exemplo, a base 2 logaritmo de 32 é 5, porque 5 é o expoente que temos de aplicar a 2 para obter 32. Uma vez que {2}^{5}=32, podemos escrever {\mathrm{log}}_{2}32=5. Lemos isto como “log base 2 de 32 é 5″.”
Podemos expressar a relação entre a forma logarítmica e a sua forma exponencial correspondente da seguinte forma:
{\mathrm{log}}_{b}{esquerda(x=direita)=y\ seta de esquerda-direita {b}^{y}=x,{\b>0,b\ne 1
p>Nota que a base b é sempre positiva.
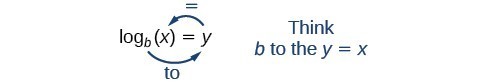
Porque um logaritmo é uma função, está mais correctamente escrito como {\mathrm{log}_{b}{esquerda(x=direita) usando parênteses para denotar a avaliação da função tal como nós o faríamos com f=esquerda(x=direita). Contudo, quando a entrada é uma única variável ou número, é comum ver os parênteses descartados e a expressão escrita sem parênteses como {\i1}_{b}x. Note-se que muitas calculadoras requerem parênteses em torno do x.
Podemos ilustrar a notação de logaritmos da seguinte forma:
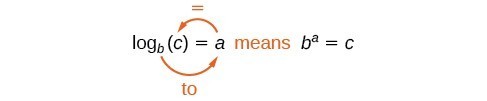
Notem que ao comparar a função logaritmo e a função exponencial, a entrada e a saída são trocadas. Isto significa y={\mathrm{log}}_{b}{esquerda(x\direita) e y={b}^{x} são funções inversas.
A Nota Geral: Definição da Função Logarítmica
Uma base logarítmica b de um número positivo x satisfaz a seguinte definição:
Para x>0,b>0,b\ne 1,
y={\mathrm{log}}_{b}{esquerda(x=direita){ é igual a }{b}^{y}=x, onde
- lemos {\mathrm{log}}_{b}{esquerda(x)direita} como, “o logaritmo com base b de x” ou o “log base b de x”.”
- o logaritmo y é o expoente ao qual b deve ser elevado para obter x.
- se não for indicada nenhuma base b, assume-se que a base do logaritmo é 10.
também, uma vez que as funções logarítmica e exponencial mudam os valores x e y, o domínio e o alcance da função exponencial são trocados pela função logarítmica. Portanto,
- o domínio da função logarítmica com base b { is}left(0,infty { is}lefty}.
- o intervalo da função logarítmica com base b { is}left(-infty ,infty {infty}right).
Q & A
Podemos tomar o logaritmo de um número negativo?
Não. Porque a base de uma função exponencial é sempre positiva, nenhuma potência dessa base pode ser negativa. Nunca podemos tomar o logaritmo de um número negativo. Também, não podemos tomar o logaritmo de zero. As calculadoras podem produzir um logaritmo de um número negativo quando em modo complexo, mas o logaritmo de um número negativo não é um número real.
Como fazer: Dada uma equação em forma logarítmica {\mathrm{log}}_{b}{esquerda(x\direita)=y, convertê-la para forma exponencial
- Examinar a equação y={\mathrm{log}}_{b}x e identificar b, y, e x.
- Reescrever {\mathrm{log}}_{b}x=y como {b}^{y}=x.
Exemplo: Conversão do formulário logarítmico para o formulário exponencial
Escrever as seguintes equações logarítmicas em forma exponencial.
- {\mathrm{log}}_{6}esquerda(sqrt{6}{6}direita)=frac{1}{2}
li>{\mathrm{log}_{3}{3}esquerda(9}direita)=2
Try It
Escreve as seguintes equações logarítmicas de forma exponencial.
- {\mathrm{log}}_{10}{esquerda(1.000),000\direita)=6
>{\mathrm{log}}_{5}esquerda(25\direita)=2/ol>
Converter de forma exponencial para logarítmica
Para converter de forma exponencial para logarítmica, seguimos os mesmos passos no sentido inverso. Identificamos a base b, exponencial x, e a saída y. Depois escrevemos x={\mathrm{log}}_{b}{esquerda(y\direita).
Exemplo: Conversão do formulário exponencial para o formulário logarítmico
Escrever as seguintes equações exponenciais em forma logarítmica.
- {2}^{3}=8
- {5}^{2}=25
- {10}^{-4}==frac{1}{10,000}
Try It
Escreve as seguintes equações exponenciais em forma logarítmica.
- {3}^{2}=9
- {5}^{3}=125
- {2}^{-1}==frac{1}{2}
Contributo!
Melhorar esta páginaAprenda Mais