10.2 – Métodos de Autocorrelação e Séries Temporais

Uma forma comum de falhar a condição de “independência” num modelo de regressão linear múltipla é quando os dados da amostra tiverem sido recolhidos ao longo do tempo e o modelo de regressão não conseguir captar eficazmente quaisquer tendências temporais. Em tal circunstância, os erros aleatórios no modelo são frequentemente correlacionados positivamente ao longo do tempo, de modo que cada erro aleatório é mais provável que seja semelhante ao erro aleatório anterior que seria se os erros aleatórios fossem independentes uns dos outros. Este fenómeno é conhecido como autocorrelação (ou correlação em série) e pode por vezes ser detectado traçando os resíduos do modelo em relação ao tempo. Vamos explorar mais aprofundadamente esta questão nesta secção e na próxima.

Uma série temporal é uma sequência de medições da(s) mesma(s) variável(s) feita(s) ao longo do tempo. Normalmente, as medições são feitas a intervalos regulares – por exemplo, mensal ou anual. Consideremos primeiro o problema em que temos uma variável y medida como uma série cronológica. Como exemplo, podemos ter y uma medida de temperatura global, com medições observadas todos os anos. Para enfatizar que temos valores medidos ao longo do tempo, utilizamos “t” como subscrito em vez do habitual “i”, ou seja, y_t] significa medido no período de tempo. Um modelo autoregressivo é quando um valor de uma série temporal é regressivo sobre valores anteriores dessa mesma série temporal. por exemplo, \(y_{t}}) sobre \(y_{t-1}\):

\

Neste modelo de regressão, a variável de resposta no período de tempo anterior tornou-se o preditor e os erros têm as nossas suposições habituais sobre erros num modelo simples de regressão linear. A ordem de uma autoregressão é o número de valores imediatamente anteriores na série que são utilizados para prever o valor no momento actual. Portanto, o modelo precedente é uma autoregressão de primeira ordem, escrita como AR(1).

Se quisermos prever \(y\) este ano (y_{t}), utilizando medições da temperatura global nos dois anos anteriores (\\t-1,y_{t-2}), então o modelo autoregressivo para o fazer seria o modelo autoregressivo:

>p> Este modelo é uma autoregressão de segunda ordem, escrita como AR(2), uma vez que o valor no momento $t$ é previsto a partir dos valores por vezes {t-1} e {t-2}). Mais genericamente, uma autoregressão de ordem, escrita como AR(k), é uma regressão linear múltipla na qual o valor da série em qualquer altura t é uma função (linear) dos valores por vezes ^(t-1,t-2,^ldots,t-k).

Autocorrelação e Autocorrelação Parcial

O coeficiente de correlação entre dois valores numa série temporal é chamado função de autocorrelação (ACF) Por exemplo, a ACF para uma série temporal \(y_t\) é dada por:

\

Este valor de k é o intervalo de tempo a ser considerado e é chamado de desfasamento. Uma autocorrelação lag 1 (i.e., k = 1 no acima) é a correlação entre valores que estão separados por um período de tempo. Mais geralmente, uma autocorrelação lag k é a correlação entre valores que são k períodos de tempo separados.

A ACF é uma forma de medir a relação linear entre uma observação no tempo t e as observações em tempos anteriores. Se assumirmos um modelo AR(k), então podemos desejar medir apenas a associação entre \(y_{t}} e \(y_t-k}) e filtrar a influência linear das variáveis aleatórias que se encontram entre elas (i.e., \i(y_{t-1},y_{t-2},\i(k-1 )}), o que requer uma transformação na série temporal. Depois, calculando a correlação das séries cronológicas transformadas obtemos a função de autocorrelação parcial (PACF).

O PACF é mais útil para identificar a ordem de um modelo autoregressivo. Especificamente, as autocorrelações parciais de amostra que são significativamente diferentes de 0 indicam termos desfasados de \\(y) que são preditores úteis de \(y_{t}). É importante que a escolha da ordem faça sentido. Por exemplo, suponha que tenha leituras de tensão arterial para cada dia durante os últimos dois anos. Poderá descobrir que um modelo AR(1) ou AR(2) é apropriado para modelar a tensão arterial. Contudo, o PACF pode indicar um grande valor de autocorrelação parcial com um atraso de 17, mas uma encomenda tão grande para um modelo autoregressivo provavelmente não faz muito sentido.

Exemplo 1: Google Data

O conjunto de dados (google_stock.txt) consiste em n = 105 valores que são o preço de fecho de uma acção do Google durante 2-7-2005 a 7-7-2005. Vamos analisar o conjunto de dados para identificar a ordem de um modelo autoregressivo. Um gráfico dos preços das acções versus tempo é apresentado na figura abaixo:

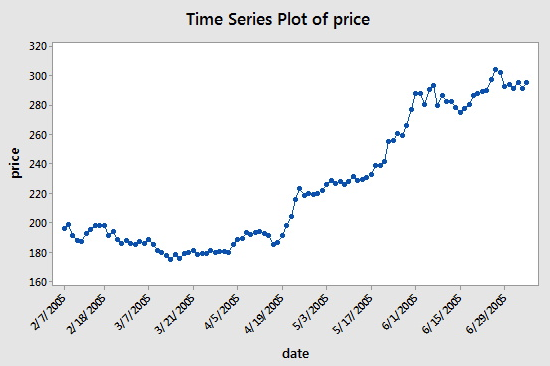
Valores consecutivos parecem seguir-se bastante de perto, sugerindo que um modelo de autoregressão poderia ser apropriado. Seguidamente olhamos para um gráfico de autocorrelações parciais para os dados:

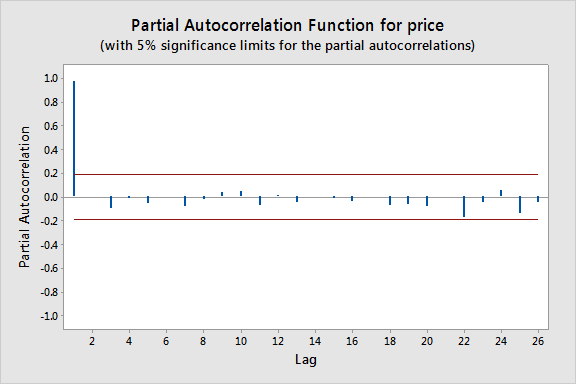
Aqui notamos que há um pico significativo com um atraso de 1 e muito mais baixo para os atrasos subsequentes. Assim, um modelo AR(1) seria provavelmente viável para este conjunto de dados.

Alfimartos aproximados também podem ser construídos (como dado pelas linhas vermelhas na parcela acima) para que esta parcela ajude a determinar grandes valores. Os limites de significância aproximados são dados por z_{1-{1-alfa-/2}/sqrt{n}). Os valores fora de qualquer destes limites são indicativos de um processo autoregressivo.

A seguir criamos uma variável de preço lag-1 e consideramos um gráfico de dispersão de preço em relação a esta variável lag-1:

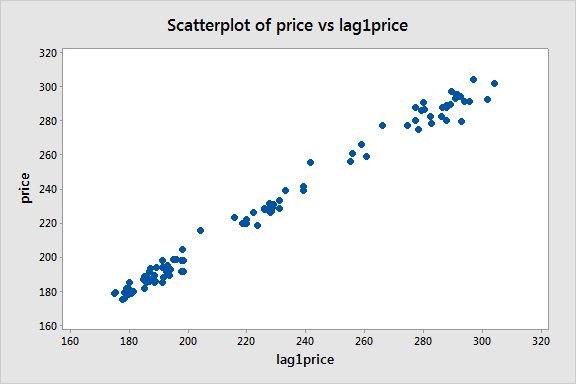
Parece haver um forte padrão linear, afirmando que o modelo autoregressivo de primeira ordem

p>p>p>pode ser útil.

Exemplo 2: Dados Quake

Let yt = o número anual de terramotos com magnitude superior a 7 na escala Richter durante n = 100 anos (dados sísmicos.txt obtidos de https://earthquake.usgs.gov). O gráfico abaixo dá um gráfico de série temporal para este conjunto de dados.

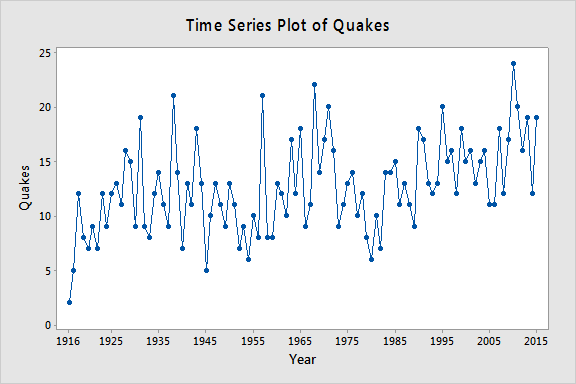
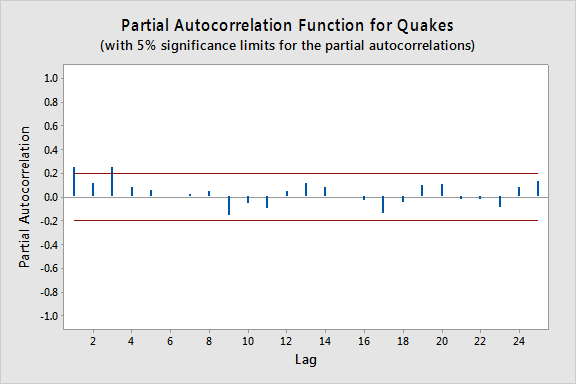
O gráfico abaixo dá um gráfico do PACF (função de autocorrelação parcial), que pode ser interpretado como significando que uma autocorrelação de terceira ordem pode ser justificada uma vez que existem notáveis autocorrelações parciais para os desfasamentos 1 e 3.

O passo seguinte é fazer uma regressão linear múltipla com número de abalos como variável de resposta e lag-1, lag-2, e lag-3 abalos como variáveis preditoras. Nos resultados abaixo vemos que o preditor lag-3 é significativo ao nível 0,05 (e o valor p do preditor lag-1 é também relativamente pequeno).