32-bit ALU
Ao introduzir valores numéricos nos campos de resposta, pode usarinteiros (1000, 0x3E8, 0b1111101000), números de ponto flutuante(1000.0), notação científica (1e3), factores de escala de engenharia(1K), ou expressões numéricas (3*300 + 100). Links úteis:
- Introdução a Jade
- Biblioteca de Células Padrão
Problema 1. Problema de Design: Unidade Aritmética e Lógica de 32 bitsVer as instruções abaixo. Use a instância Jade abaixo para introduzir o seu design. Para completar este problema de design, seleccione o módulo /alu/alu e clique na barra de ferramentas de Jade e o testador incorporado irá reportar quaisquer discrepâncias entre os resultados esperados e reais, ou, se o seu design estiver correcto, irá registar o teste aprovado.{ “shared_modules”: “hierárquico”: “verdadeiro”, “partes”: , “ferramentas”: , “editores”: , “editores”: , “edit”: , “edit”: “/alu/alu”, “required_tests”: } Neste laboratório, vamos construir a unidade aritmética e lógica (ALU) para o processador Beta. A ALU tem duas entradas de 32 bits (a que chamaremos “A” e “B”) e produz uma saída de 32 bits. Começaremos por desenhar cada peça da ALU como um circuito separado, cada uma produzindo a sua própria saída de 32 bits. Depois combinaremos estas saídas num único ALUresultado.Ao desenhar circuitos há três factores separados que podem ser optimizados:
- desenho para desempenho máximo (latência mínima)
- desenho para a melhor relação custo/desempenho (área mínima*latência)
desenho para custo mínimo (área mínima)
Felizmente, é muitas vezes possível fazer os três de uma só vez, mas em algumas partes do circuito, algum tipo de troca de desenho terá de ser bem feita. Ao conceber o seu circuito deverá escolher qual dos três factores é mais importante para si e optimizar o seu design de acordo com as suas necessidades. A biblioteca de células padrão & simulação a nível de portasOs blocos de construção para este laboratório provêm de uma biblioteca de portas lógicas – os fabricantes de circuitos integrados têm frequentemente uma “biblioteca de células padrão” e ferramentas de desenho variadas para facilitar aos seus clientes a concepção sem se preocuparem com a geometria detalhada das camadas de máscara utilizadas para criar mosfets e cabos. 6.004 tem a sua própria Biblioteca de Células Padrão que fornece:
2-, 3- e 4-input AND, OR, NAND e NOR gates
2-input XOR e XNOR gates
2:1 e 4:1 multiplexors
D-register e D-latches
Ver a documentação da biblioteca para detalhes sobre as ligações apropriadas para cada porta. Em Jade, os portões da biblioteca de células padrão podem ser encontrados no contentor de peças em “/gates/”.
Uma vez que estamos a projectar ao nível do portão, podemos utilizar um fastersimulador que só conhece os portões e os valores lógicos (em vez de transístores e tensões). Note que a sua concepção não pode conter nenhummosfets, resistências, condensadores, etc.; o simulador ao nível do portão apenas suporta os primitivos do portão na biblioteca de células padrão.As entradas ainda são especificadas em termos de tensões (para manter a compatibilidade da lista de contactos com os outros simuladores), mas o simulador de nível de porta converte as tensões em um de três possíveis valores lógicos utilizando os limiares vil e vih especificados no início do seu ficheiro de desenho:
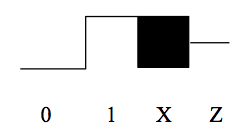
1 lógico alto (tensões maiores ou iguais ao limiar vih)
X desconhecido ou indefinido (tensões entre os limiares, ou tensões desconhecidas)
Um quarto valor “Z” é usado para representar o valor dos nós que não são movidos por nenhuma saída de porta (e.g., as saídas dos tristatedrivers que não estão activadas). O diagrama seguinte mostra como estes valores aparecem na visualização da forma de onda:
especificação ALU 
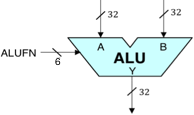A ALU de 32 bits que iremos construir será um componente no Betaprocessador que iremos abordar em laboratórios subsequentes. O símbolo lógico para a nossa ALU é mostrado à direita. É um circuito combinado tomando duas palavras de dados de 32 bits A e B como entradas, e produzindo uma saída de 32 bits Y ao executar uma aritmética especificada ou uma função lógica nas entradas A e B. A função específica a beperformar é especificada por uma entrada de controlo de 6 bits, FN, cujo valor codifica a função de acordo com a tabela seguinte:
| FN | Operation | Output value Y |
|---|---|---|
| 00-011 | CMPEQ | Y = (A == B) |
| CMPLT | Y = (A < B) | |
| Y = (A ≤ B) | ||
| 32-bit ADD | Y = A + B | |
| 01—1 | 32-bit SUBTRACT | Y = A – B |
| 10abcd | Bit-wise Boolean | Y>Y = Fabcd(A,B) |
| 11–00 | Deslocamento Lógico à esquerda (SHL) | Y>Y = A << B |
| 11–01 | Desvio Lógico à direita (SHR) | Y>Y = A >> B |
| 11–11 | Shift Aritmético direito (SRA) | Y>Y = A >> B (sinal estendido) |
Note que especificando um valor apropriado para o FNinput de 6 bits, a ALU pode realizar uma variedade de operações aritméticas, comparações, turnos, e combinações booleanas bitwise requeridas pelo nosso processadorBeta.
| Bi | Ai | |
| d | ||
| 0 | c | |
| 1 | 0 | b |
| 1 | 1 | a |
As operações booleanas bitwise são especificadas por FN=10; neste caso, os bits FN restantes abcd são tomados como testemunhos na tabela da verdade descrevendo como cada bit de Y é determinado pelos bits correspondentes de A e B, como mostrado à direita.As três operações de comparação produzem, cada uma, uma saída booleana. Nestes casos, Y são todos zero, e o bit de baixa ordem Y é um 0 ou 1 reflectindo o resultado da comparação entre os operandos de 32 bits A e B. Podemos abordar o desenho da ALU decompondo-o em subsistemas concebidos para aritmética, comparação, Booleano, e operações de deslocamento mostradas abaixo:
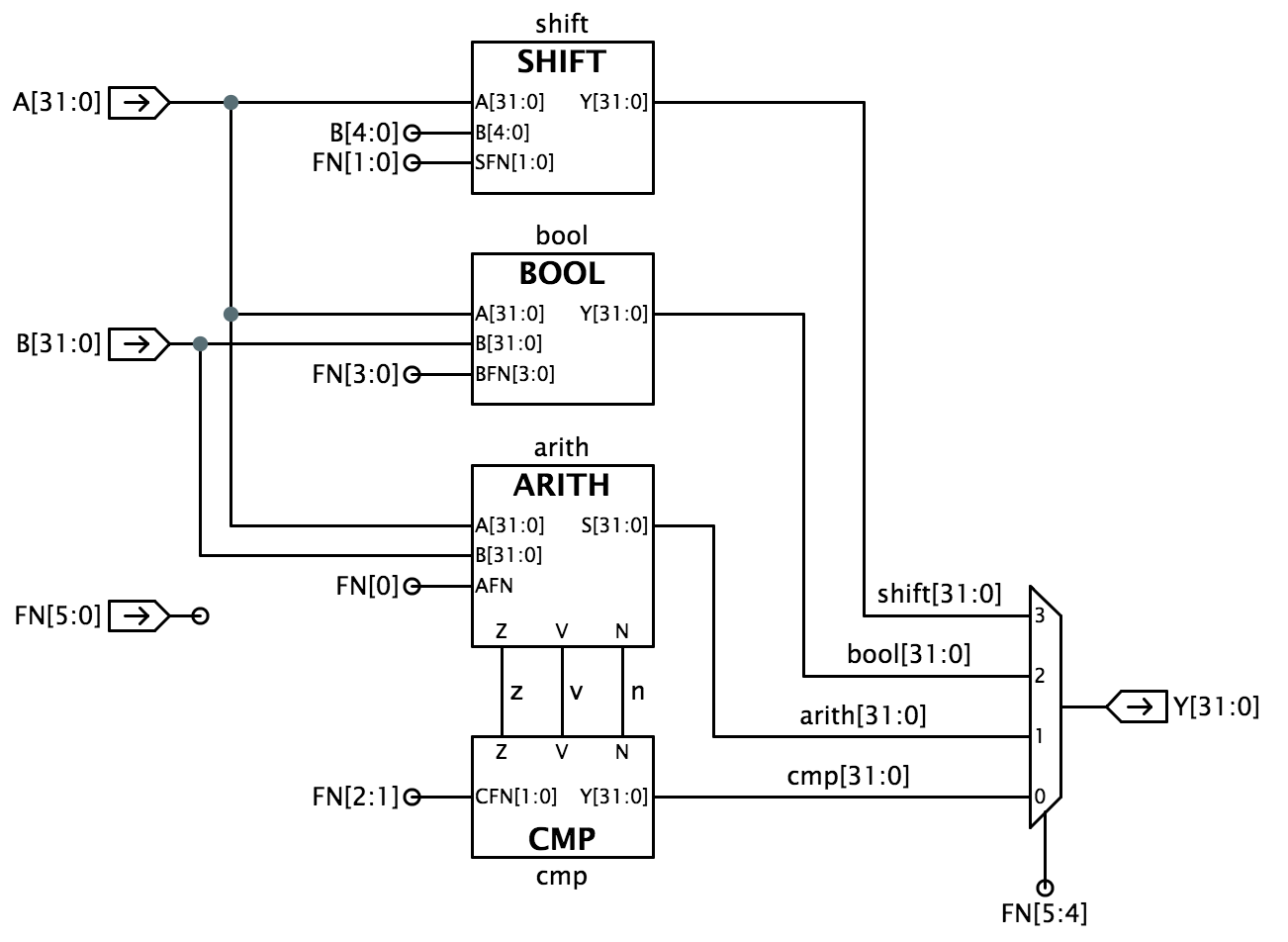A concepção de um sistema complexo como uma UAL é melhor feita por fases, permitindo que os subsistemas individuais sejam concebidos e depurados um de cada vez. Os passos abaixo seguem essa abordagem para implementar o diagrama ALUblock mostrado acima. Começamos por implementar um ALUframework com módulos dummy para cada um dos quatro principais subsistemas (BOOL, ARITH, CMP, e SHIFT); depois implementamos e depuramos versões de trabalho real de cada subsistema. Para o ajudar a seguir este caminho, realizamos testes separados para cada um dos quatro módulos componentes. NOTA: os sinais FN utilizados para controlar o funcionamento do circuito ALU utilizam uma codificação escolhida para tornar o desenho do circuito ALU simples. Esta codificação não é a mesma que a utilizada para codificar o campo de código opcode de 6 bits das instruções Beta. No Laboratório 5, construir-se-á alguma lógica (na realidade uma ROM) que traduzirá o campo de opcode de uma instrução nos bits de controlo FN apropriados. Há notas de desenho abaixo sugerindo como proceder ao desenho de cada um dos sub-módulos. Unidade BOOL Conceber o circuito para implementar as operações booleanas para a sua ALU e utilizá-lo para substituir o jumper e o fio que liga o Youtput à terra. 
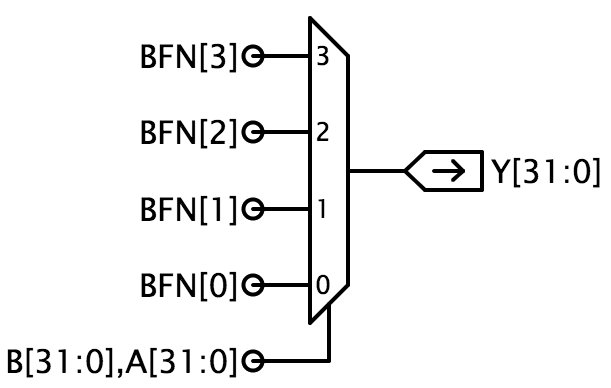A implementação sugerida utiliza 32 cópias de um multiplexor 4-to-1 (mux4) onde BFN codifica a operação a ser executada e A e B são ligados às entradas de selecção do multiplexor. Esta implementação pode produzir qualquer uma das 16 funções Booleanfunções de 2 entradas.
A tabela seguinte mostra as codificações para alguns dos sinais de controlo BFN usados pelo jig de teste (e nas nossas Betaimplementações típicas):
| Operation | BFN |
|---|---|
| AND>/td> | 1000 |
| OR | 1110 |
| XOR | 0110 |
| 1010 |
O teste BOOL verifica efectivamente todas as 16 operações booleanas numa selecção de argumentos, e comunicará quaisquer erros que encontre.Quando o seu circuito BOOL tiver sido introduzido, execute o teste clicando na marca de verificação verde; deve aparecer uma janela de gráfico de simulação mostrando as entradas e saídas. Jade verificará os resultados do seu circuito em relação a uma lista de valores inesperados e relatará quaisquer discrepâncias que encontre.
unidade ARITHDesenhar uma unidade adder/subtractor (ARITH) que funciona nas entradas do complemento de 32-bittwo e gera uma saída de 32-bit. Será útil gerar outros três sinais de saída para serem utilizados pela unidade CMP: Z que é verdadeiro quando as saídas S são allzero, V que é verdadeiro quando a operação de adição transborda (ou seja, o resultado é demasiado grande para ser representado em 32 bits),e N que é verdadeiro quando a soma é negativa (ou seja S = 1) O overflow nunca pode ocorrer quando os dois operandos da adição têm sinais diferentes; se os dois operandos têm o mesmo sinal, então o overflow pode ser detectado se o sinal do resultado for diferente do sinal dos operandos:
AFN será definido como 0 para um ADD (\(S = A+B\)) e 1 para aSUBTRACT (\(S = A-B\)); A e B são os operandos de entrada do complemento de 32 bits; S é o resultado de 32 bits; Z/V/N são os três codebits de condição descritos acima. Vamos utilizar a convenção de numeração de bits “little-endian” onde o bit 31 é o bit mais significativo e o bit0 é o bit menos significativo. Fornecemos um módulo FA para entrar no esquema de nível de porta para a víbora completa (ver Problema 8 do Laboratório #1) para ser utilizado na construção da víbora de 32 bits que forma o coração da unidade ARITH. O sinal de entrada AFN selecciona se a operação é um ADD ou SUBTRACT. Para fazer um SUBTRACTO, o circuito calcula primeiro a negação do complemento de dois do operando B invertendo B e depois adicionando um (o que pode ser feito forçando o transporte da adição de 32 bits a ser 1). Comece por implementar a adição de 32 bits utilizando a arquitectura de aripple-carry (mais tarde, poderá melhorar isto no curso). Terá de construir a porta NOR de 32 bits necessária para calcular Z usando uma árvore de portas de ventilação mais pequenas (a biblioteca de peças só tem portas com até 4 entradas). Ao entrar nos seus circuitos, lembre-se de apagar os saltas originais e os fios que ligaram as saídas à terra! O teste do módulo tenta adicionar e subtrair vários operandos, assegurando que as saídas Z, V e N são correctas após cada operação. Unidade CMPA ALU fornece três operações de comparação para os operandos A e Boperands. Podemos utilizar a unidade de adição concebida acima para calcular \(A-B\)e depois olhar para o resultado (na realidade apenas os códigos de condições Z, V e N) para determinar se A=B, A < B ou A ≤ B. As operações de comparação geram um resultado de 32 bits usando o número 0 para representar o falso e o número 1 para representar o verdadeiro.Desenha uma unidade de comparação de 32 bits (CMP) que gera um de dois constantes (0 ou 1) dependendo dos sinais de controlo CFN (utilizados para seleccionar a comparação a ser realizada) e as saídas Z, V, e N da unidade viciante/subtractor. É evidente que os 31 bits de alta ordem da saída são sempre zero. O bit menos significativo (LSB) da saída é determinado pela comparação a ser efectuada e pelos resultados da subtracção efectuada pela víbora/subtractor: | Comparação | Equação para LSB | CFN |
|---|---|---|
| A = B | LSB = \(Z\) | 01 |
| A < B | ||
| LSB = \(Z + (N \oplus V)\) | 11 |
Ao nível do módulo ALU, Os FN são utilizados para controlar a unidade de comparação desde que se utilizou o FN para controlar a unidade víbora/subtractor para forçar uma subtracção.Nota de desempenho: as entradas Z, V e N neste circuito só podem ser calculadas pela unidade víbora/subtractora após a adição de 32 bits estar completa. Isto significa que chegam bastante tarde e depois requerem um processamento adicional neste módulo, o que por sua vez faz com que Y apareça muito tarde no jogo. Pode acelerar consideravelmente as coisas pensando no tempo relativo de Z, V e N e depois desenhando a sua lógica tominimizar caminhos de atraso envolvendo sinais de chegada tardia. O teste do módulo assegura que a resposta correcta é gerada para todas as combinações possíveis de Z, V, N e CFN. Unidade SHIFT Desenho de uma unidade de deslocamento de 32 bits que implementa operações de deslocamento lógico esquerdo (SHL), deslocamento lógico direito (SHR) e deslocamento aritmético direito (SRA). O operando A fornece os dados a serem deslocados e os 5 bits de ordem baixa do operando B são utilizados como contagem de deslocamento (ou seja, de 0 a 31 bits de deslocamento). A operação desejada será codificada no SFN como se segue:
| Operation | SFN |
|---|---|
| SHL (shift left) | 00 |
| SHR (shift direita) | 01 |
| 11 |
Com esta codificação, O SFN é 0 para um turno da esquerda e 1 para um turno da direita e o SFN controla a lógica de extensão do sinal no turno da direita. Para SHL e SHR, os 0’s são deslocados para os postos de bits vagos. Para SRA (“shift right arithmetic”), as posições de bits vagas são todas preenchidas com A, o bit de sinal dos dados originaiso que o resultado será o mesmo que dividir os dados originais pelo poder apropriado de 2.A implementação mais simples é construir dois turnos – um para a esquerda e outro para a direita – e depois usar um multiplexador de 32 bits de 2 vias para seleccionar a resposta apropriada como saída do módulo. É fácil de construir um shifter depois de reparar que o amulti-bit shift pode ser realizado por mudanças em cascata por variouspowers de 2. Por exemplo, um shift de 13 bits pode ser implementado por ashift de 8, seguido por um shift de 4, seguido por um shift de 1. Sothe shifter é apenas uma cascata de multiplexadores, cada um controlado por onebit da contagem de turnos. O esquema abaixo mostra uma possível implementação da lógica do turno esquerdo; a lógica do turno direito é semelhante com a ligeira complicação adicional de ter de mudar em 0 (ou seja, “gnd”) ou A, dependendo do valor doSFN. Outra abordagem que poupa os portões é utilizar a lógica do turno esquerdo para ambos os turnos, mas para os turnos direito, inverter os bits do operando A na entrada e inverter os bits da saída na saída.
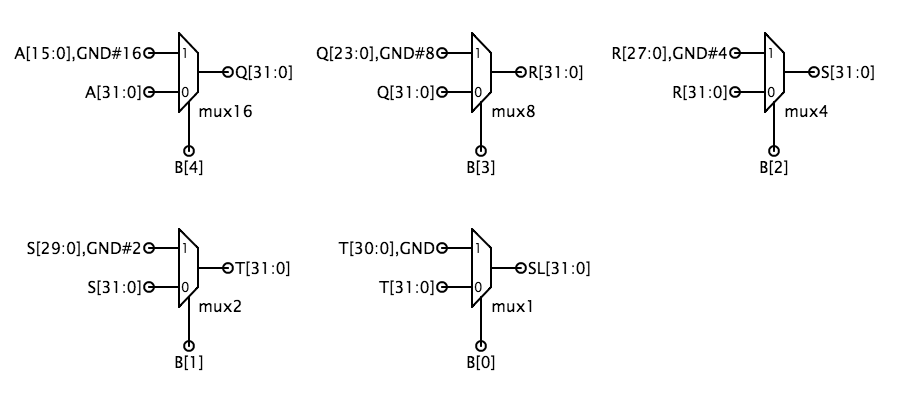O teste do módulo verifica se os três tipos de turnos estão a funcionar correctamente. Testes finais Quando tiver concluído a concepção dos quatro sub-módulos, seleccione o módulo ALU e execute o seu teste. Este executa cada um dos conjuntos de teste que utilizou para depurar os subcircuitos dos componentes, portanto, a menos que haja alguma interacção imprevista entre os seus blocos, é provável que passe no teste. Quando este teste for concluído com êxito, o sistema marcará a sua concepção como completa. Problema 2. Testando a ALUNo problema de concepção deste laboratório (ver acima), estará a construir uma unidade aritmética e lógica (ALU) de 32 bits que realiza operações aritméticas e lógicas em operandos de 32 bits, produzindo um resultado de 32 bits. O teste para este laboratório verifica o seu circuito ALU através da aplicação de 186 conjuntos diferentes de valores de entrada. Esta pergunta explora a forma como esses valores foram escolhidos. Nenhum designer que eu conheça pensa que testar é divertido – desenhar o circuito parece muito mais interessante do que ter a certeza que funciona. Lembre-se que um bom engenheiro não só sabe como construir bons desenhos mas também constrói bons desenhos, e isso significa testar o desenho para ter a certeza de que faz o que diz fazer.Uma forma óbvia de testar um circuito combinado é experimentar todas as combinações possíveis de entradas, verificando os valores de saída correctos depois de aplicar cada combinação de entradas. Este tipo de teste exaustivo prova o funcionamento correcto, enumerando a tabela de verdade do dispositivo combinado. Esta é uma estratégia de trabalho para circuitos com poucas entradas mas rapidamente se torna impraticável para circuitos com muitas entradas. Ao tirar partido da informação sobre como o circuito é construído, podemos reduzir consideravelmente o número de combinações de entradas necessárias para testar o circuito. A arquitectura de víbora de ondulação sugerida no Problema de Concepção utiliza 32 cópias do módulo de víbora completo para criar uma víbora de 32 bits. Cada víbora completa tem 3 entradas (A, B, CI) e duas saídas (S, CO):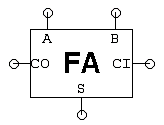 
- Um único vector de teste para a víbora completa consiste em 3 valores de entrada (um para A, B e CI) e 2 valores de saída (S e CO). Para executar um teste, os valores de entrada do vector de teste actual são aplicados ao dispositivo em teste e depois os valores de saída reais são comparados com os valores esperados listados pelo vector de teste. Este processo é repetido até que todos os vectores de teste tenham sido utilizados. Assumindo que não sabemos nada sobre o circuito interno da víbora completa, quantos vectores de teste seriam necessários para testar exaustivamente a sua funcionalidade? Número de vectores de teste para testar exaustivamente a víbora completa?
- Considerar um adder de 32 bits com 64 entradas (dois operandos de entrada de 32 bits, assumir que o CIN está ligado à terra como mostra o diagrama abaixo) e 32 saídas (o resultado de 32 bits). Assumir que não sabemos nada sobre o circuito interno e por isso não podemos descartar a possibilidade de que possa obter a resposta errada para qualquer combinação particular de entradas. Por outras palavras, só porque o viciador obteve a resposta correcta para 2 + 3 não nos permite tirar quaisquer conclusões sobre qual a resposta que obteria para 2 + 7. Se pudéssemos aplicar um vector de teste a cada 100ns, quanto tempo demoraria a testar exaustivamente a víbora? Tempo para testar exaustivamente a víbora de 32 bits? (em anos)
- Três das entradas da unidade de comparação (Z, V e N) provêm do adder/subtractor em execução no modo de computação de subtracção A-B:
li>Claramente, testar uma víbora de 32 bits experimentando todas as combinações de valores de entrada não é um bom plano! Abaixo está apresentado um esquema para uma víbora de 32-bit.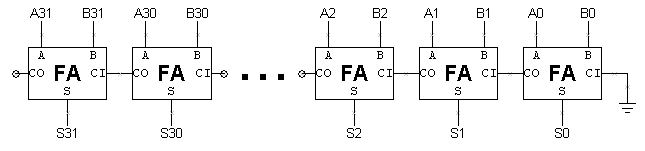 
Excepto no transporte do bit para a direita, cada bit da víbora funciona independentemente. Podemos usar esta observação para testar a víbora bit a bit e com um pouco de reflexão podemos realmente executar muitos destes testes em paralelo. Neste caso, o facto de a víbora ter obtido a resposta correcta para 2 + 3 diz-nos realmente muito sobre a resposta que obterá para 2 + 7. Uma vez que o cálculo feito pelos bits 0 e 1 da víbora é o mesmo em ambos os casos, se a resposta para 2 + 3 estiver correcta, os dois bits de baixa ordem da resposta para 2 + 7 também estarão correctos. Assim, o nosso plano para testar a víbora de ondulação é testar cada víbora completa de forma independente. Ao testar o bit N, podemos definir A e B directamente do vector de teste. É preciso um pouco mais de trabalho para definir CI para um determinado valor, mas podemos fazê-lo com as escolhas correctas para A e B. Se quisermos definir CI para 0, que valores devem ser definidos para A e B? Se quisermos definir o IC para 1? Suponha que não podemos assumir nada sobre o valor do IC. Valores de A e B para fazer C=0? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Valores de A e B para fazer C=1? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Com esta estratégia, podemos testar os bits pares da víbora em paralelo com um conjunto de vectores de teste e testar os bits ímpares da víbora em paralelo com outro conjunto de vectores de teste. Aqui está um conjunto de 10 vectores de teste que devem testar todas as combinações de valores de entrada para cada FA de uma víbora de 32 bits:
| bits 0, 2, … | bits 1, 3, … | A | B |
|---|---|---|---|
| A=0, B=0, CI=0 | A=0, B=0, CI=0 | 0x00000000 | 0x00000000 |
| A=1, B=0, CI=0 | A=0, B=0, CI=0 | 0x00000000 | |
| A=0, B=1, CI=0 | A=0, B=0, CI=0 | 0x00000000 | 0x55555555 |
| A=1, B=1, CI=0 | A=0, B=0, CI=1 | 0x55555555 | 0x5555555555 |
| A=0, B=0, CI=0 | A=1, B=0, CI=0 | 0xAAAAAA | 0x00000000 |
| A=0, B=0, CI=0 | A=0, B=1, CI=0 | 0x00000000 | 0xAAAAAA |
| A=0, B=0, CI=1 | A=1, B=1, CI=0 | 0xAAAAAAA | 0xAAAAAAA |
| A=1, B=0, CI=1 | A=1, B=0, CI=1 | 0xFFFFFFFF | 0x00000001 |
| A=0, B=1, CI=1 | A=0, B=1, CI=1 | 0x00000001 | 0xFFFFFFFF |
| A=1, B=1, CI=1 | A=1, B=1, CI=1 | 0xFFFFFFFFFF | 0xFFFFFFFFFF |
| Bi | Ai | Yi |
| 0 | 1 | c |
| 1 | 0 | b |
| 1 | 1 | a |
Como vimos nas instruções para a UAL,as operações bitwise booleanas são especificadas por FN=10. Neste caso, os bits FN restantes abcd são tomados como testemunhas na tabela da verdade descrevendo como cada bit de Y é determinado pelos bits correspondentes de A e B, como mostrado à direita. Para cada uma das operações booleanas \(F(A,B)\) especificadas abaixo, determinar as definições para FN de modo a que a unidade Bool calcule a operação desejada. AND(A,B){(A,B): FN= 0000 0001 0010 0011 0100 0101 0101 0110 0111 1000 1001 1010 1011 1100 1101 1101 1110 1111 OU(A,B): FN= 0000 0001 0001 0010 0011 0100 0101 0101 0110 0111 1000 1001 1010 1011 1100 1101 1101 1110 1111 XOU(A,B): FN= 0000 0001 0010 0010 0011 0100 0101 0101 0110 0111 1000 1001 1010 1011 1100 1101 1101 1110 1111 NAND(A,B): FN= 0000 0001 0010 0010 0011 0100 0101 0101 0110 0111 1000 1001 1010 1011 1100 1101 1101 1110 1111 NOR(A,B): FN= 0000 0001 0001 0010 0011 0100 0101 0101 0110 0111 1000 1001 1010 1011 1100 1101 1101 1110 1111 XNOR(A,B): FN= 0000 0001 0010 0011 0100 0101 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 A: FN= 0000 0001 0010 0010 0011 0100 0101 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 B: FN= 0000 0001 0010 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111