Backpropagation Step by Step

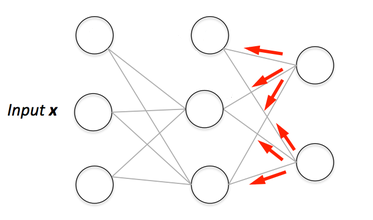Se estiver a construir a sua própria rede neural, terá definitivamente de compreender como treiná-la.Backpropagation é uma técnica comummente utilizada para o treino de rede neural. Existem muitos recursos que explicam a técnica, mas este post irá explicar a retropropagação com exemplos concretos em passos coloridos muito detalhados.

Pode ver aqui a visualização do passe para a frente e da retropropagação. Pode construir a sua rede neural utilizando o netflow.js

Overview

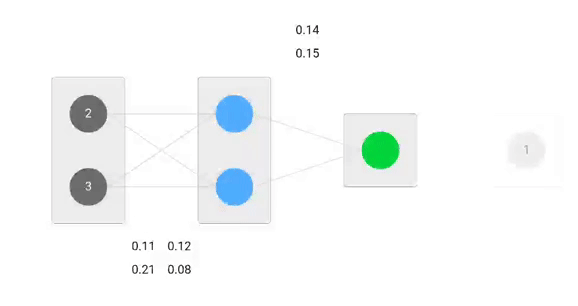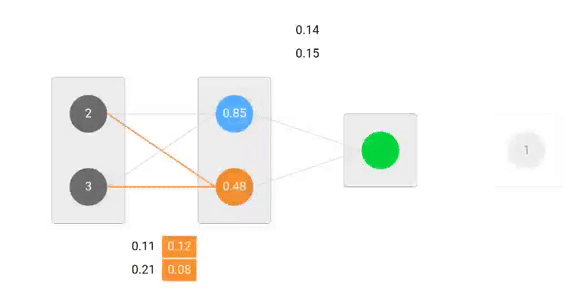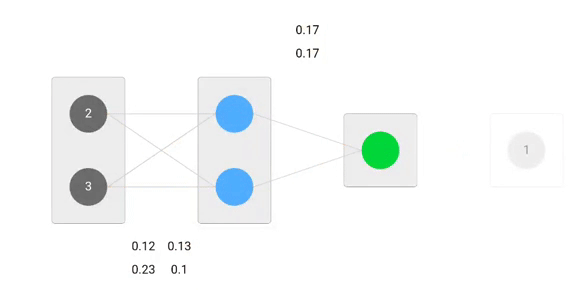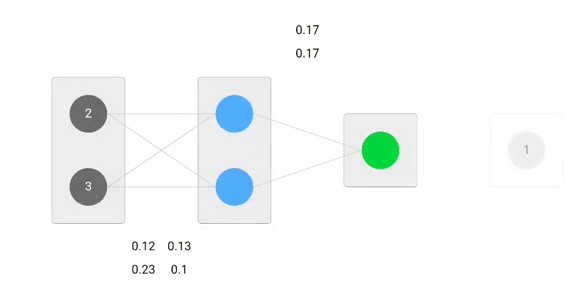
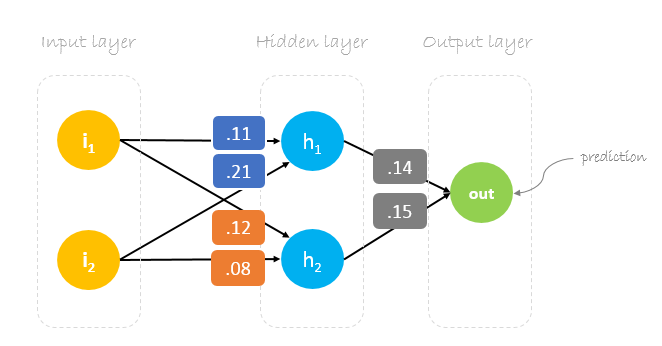
Neste post, vamos construir uma rede neural com três camadas:

• Camada de entrada com dois neurónios de entrada
• Uma camada oculta com dois neurónios
• Camada de saída com um único neurónio

div id=”0451463831″>android-tabs

Pesos, pesos, pesos

Treinamento da rede neural é sobre encontrar pesos que minimizem o erro de previsão. Normalmente começamos a nossa formação com um conjunto de pesos gerados aleatoriamente. Depois, a retropropagação é utilizada para actualizar os pesos numa tentativa de mapear correctamente as entradas arbitrárias às saídas.

Os nossos pesos iniciais serão os seguintes:w1 = 0.11w2 = 0.21w3 = 0.12w4 = 0.08w5 = 0.14 e w6 = 0.15

Dataset

O nosso conjunto de dados tem uma amostra com duas entradas e uma saída.

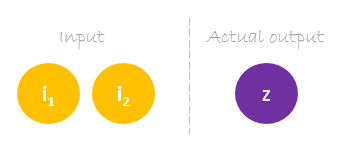
A nossa amostra única é a seguinte inputs= e output=.

p>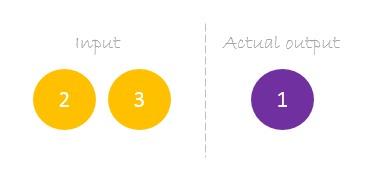

Forward Pass

Usaremos dados pesos e entradas para prever a saída. As entradas são multiplicadas por pesos; os resultados são depois passados para a camada seguinte.

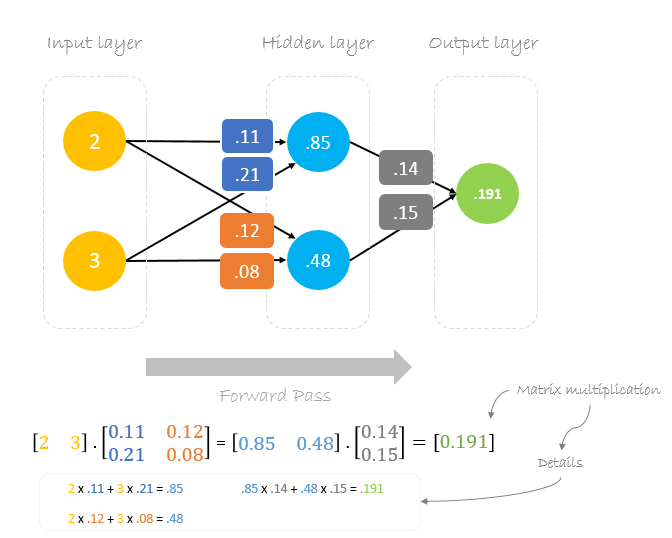
Calculating Error

Agora, é altura de descobrir como é que a nossa rede funcionava, calculando a diferença entre a saída real e a prevista. É evidente que a nossa saída da rede, ou previsão, não está nem sequer próxima da saída real. Podemos calcular a diferença ou o erro da seguinte forma.

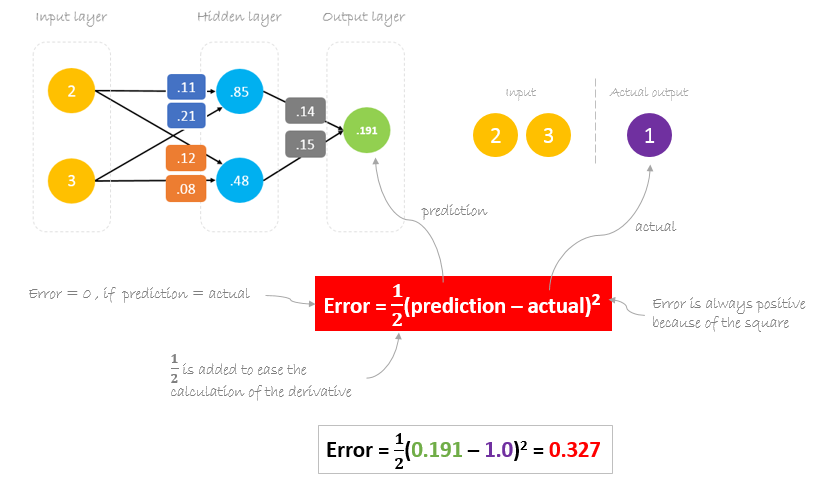
Erro Redutor

O nosso principal objectivo da formação é reduzir o erro ou a diferença entre a previsão e a produção real. Uma vez que o output real é constante, “não mudando”, a única forma de reduzir o erro é alterar o valor da previsão. A questão agora é, como alterar o valor da previsão?

Ao decompor a previsão nos seus elementos básicos, podemos descobrir que os pesos são os elementos variáveis que afectam o valor da previsão. Por outras palavras, para alterar o valor da previsão, precisamos de alterar os valores dos pesos.

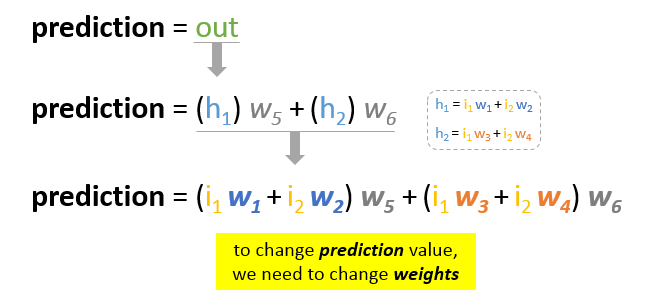
A questão agora é como alterar\ actualizar o valor dos pesos para que o erro seja reduzido?
A resposta é Backpropagation!

Backpropagation

Backpropagation, abreviatura de “propagação retroactiva de erros”, é um mecanismo usado para actualizar os pesos usando a descida de gradiente. Calcula o gradiente da função de erro em relação aos pesos da rede neural. O cálculo procede para trás através da rede.

Descida de gradiente é um algoritmo de optimização iterativo para encontrar o mínimo de uma função; no nosso caso, queremos minimizar a função de erro. Para encontrar o mínimo local de uma função utilizando a descida de gradiente, são dados passos proporcionais ao negativo do gradiente da função no ponto actual.

Por exemplo, para actualizar w6, tomamos a corrente w6 e subtraímos a derivada parcial da função erro com respeito a w6. Opcionalmente, multiplicamos a derivada da função de erro por um número seleccionado para assegurar que o novo peso actualizado está a minimizar a função de erro; a este número chama-se taxa de aprendizagem.

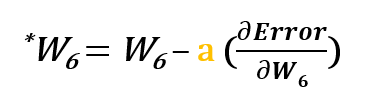
A derivação da função de erro é avaliada aplicando a regra da cadeia como se segue

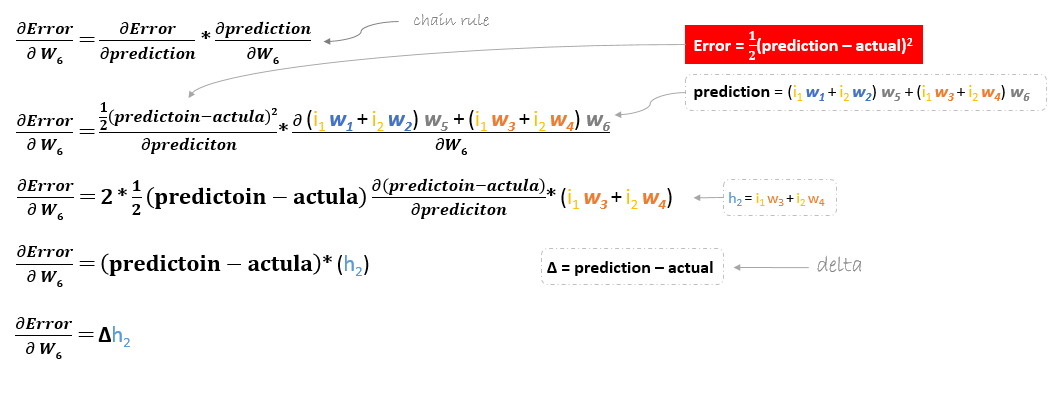
Então para actualizar w6 podemos aplicar a seguinte fórmula

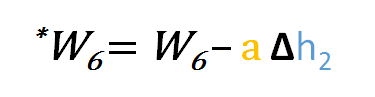
Similiarmente, podemos derivar a fórmula de actualização para w5 e quaisquer outros pesos existentes entre a saída e a camada oculta.

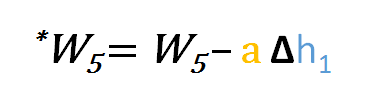
Contudo, ao recuar para actualizar w1w2w3 e w4 existente entre a camada de entrada e a camada oculta, a derivada parcial para a função de erro em relação a w1, por exemplo, será como se segue.

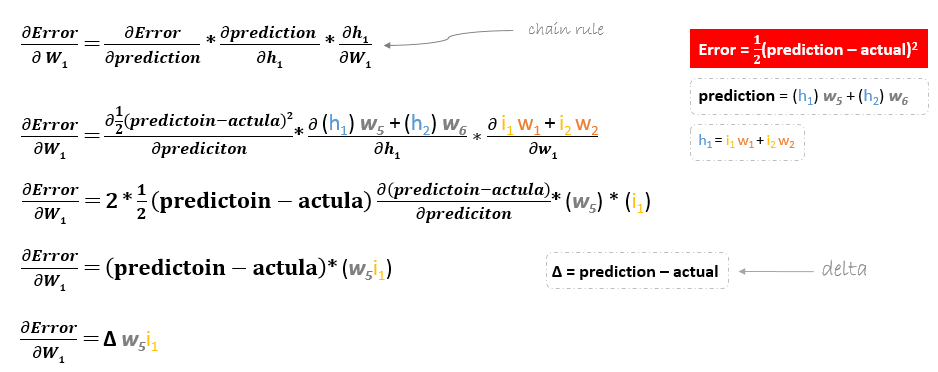
Podemos encontrar a fórmula de actualização para os pesos restantes w2w3 e w4 da mesma forma.

Em resumo, as fórmulas de actualização para todos os pesos serão as seguintes:

Podemos reescrever as fórmulas de actualização em matrizes como se segue

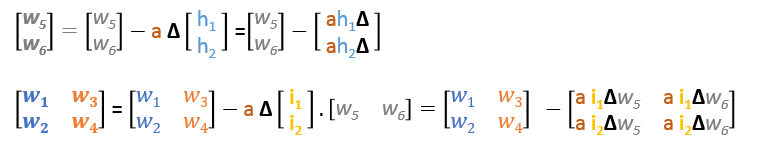
Backward Pass

Utilizando fórmulas derivadas, podemos encontrar os novos pesos.

Learning rate: é um hiperparâmetro que significa que precisamos de adivinhar manualmente o seu valor.

Now, utilizando os novos pesos repetiremos o forward passed

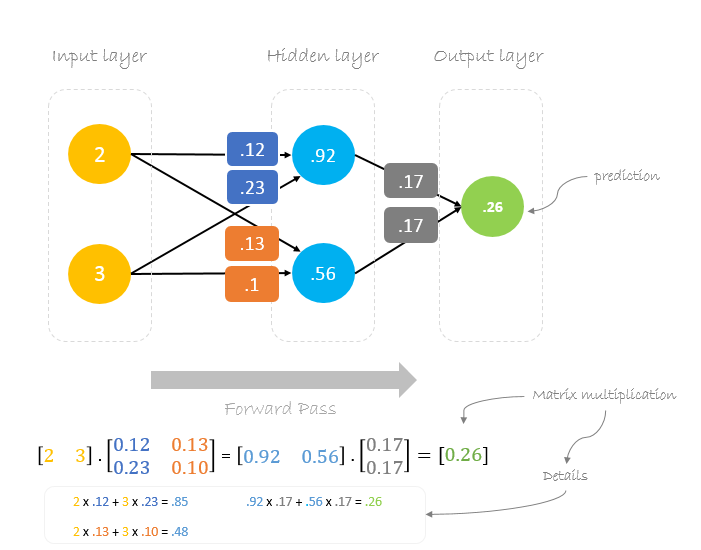
p> Podemos notar que a previsão 0.26 está um pouco mais próxima da produção real do que a anteriormente prevista 0.191. Podemos repetir o mesmo processo de passagem para trás e para a frente até o erro estar próximo ou igual a zero.

Voltarpropagação Visualização

P>Pode ver aqui a visualização da passagem para a frente e para tráspropagação.

P>Pode construir a sua rede neural usando netflow.js