Chang Hsin Lee

Quando construo um modelo de aprendizagem de máquinas para problemas de classificação, uma das questões que me faço é porque é que o meu modelo não é uma porcaria? Por vezes sinto que desenvolver um modelo é como segurar uma granada, e a calibração é um dos meus pinos de segurança. Neste post, vou percorrer o conceito de calibração, depois mostrar em Python como fazer gráficos de calibração diagnóstica.

Aqui o link para o caderno Jupyter para este post

Avaliar previsões probabilísticas

Deixem-me começar por explicar o que é a calibração e de onde veio a ideia.

Na aprendizagem de máquinas, a maioria dos modelos de classificação produzem previsões de probabilidades de classe entre 0 e 1, tendo depois uma opção de transformar os resultados probabilísticos em previsões de classe. Mesmo os algoritmos que apenas produzem pontuações como máquina vectorial de suporte, podem ser adaptados para produzir previsões probabilísticas.

Para um problema de classificação binária, existem métricas sumárias – precisão, recordação, F1-score, etc. – que avaliam a qualidade das saídas binárias 0s e 1s. Se os resultados não forem binários mas sim números flutuantes entre 0 e 1, então posso usá-los como pontuação para a classificação. Mas os números flutuantes entre 0 e 1 gritam probabilidades, e como posso saber se posso confiar neles como probabilidades?

A saída de um modelo pode ser vista como uma declaração dizendo quão provável algo deveria acontecer. Um exemplo de tal modelo – cujas declarações verifico todos os dias antes de deixar a minha casa – é o serviço meteorológico. Em particular, qual a probabilidade de chuva?

imagem do tempo.com

Diz que no domingo, há 80% de probabilidade de chuva. Quão fidedigna é esta chamada de 80%? Se eu investigar as previsões anteriores do weather.com e descobrir que 8 em 10 dias estão chuvosos quando chamam 80%, então posso convencer-me a carregar os meus audiolivros e preparar-me para o tráfego louco na auto-estrada à tarde.

Por outras palavras, uma previsão meteorológica precisa significa que se eu analisar 100 dias que estão previstos com 80% de probabilidade de chuva, então deverá haver cerca de 80 dias de chuva. Também tem de ser precisa em outras faixas de probabilidade. Para dias que são chamados a chover 30% do tempo, deve haver 30 dias de chuva em média de 100 dias. Se as previsões deste serviço de previsão meteorológica seguirem todas este bom padrão, então dizemos que as suas previsões são calibradas. É a forma probabilística de dizer que atingem o prego na cabeça.

• Um modelo probabilístico é calibrado se eu colocar as amostras de teste no caixote do lixo com base nas suas probabilidades previstas, os resultados verdadeiros de cada caixote do lixo têm uma proporção próxima das probabilidades no caixote do lixo.

Como é que eu avalio a calibração? Em vez de resumir a calibração num único número, prefiro fazer gráficos de calibração.

Gráficos de calibração são frequentemente gráficos de linha. Uma vez escolhido o número de caixas e atirado as previsões para a caixa, cada caixa é então convertida num ponto na parcela. Para cada contentor, o valor y é a proporção dos resultados reais, e o valor x é a probabilidade média prevista. Portanto, um modelo bem calibrado tem uma curva de calibração que abraça a linha recta y=x. Aqui está um exemplo de um gráfico de calibração com duas curvas, cada uma representando um modelo sobre os mesmos dados.

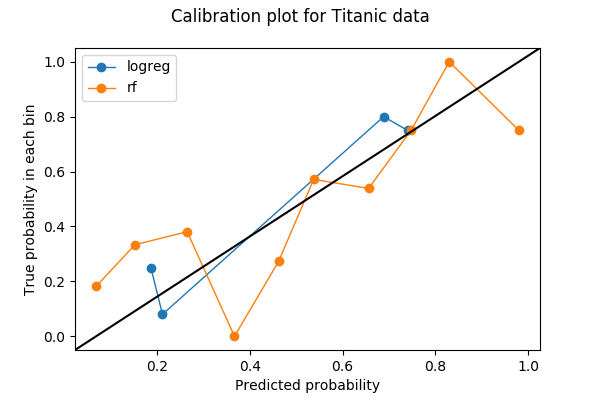
Vou mostrar como fiz este gráfico em Python e o que vi nele.

Um exemplo de Python

A primeira coisa a fazer ao fazer um gráfico de calibração é escolher o número de silos. Neste exemplo, coloquei as probabilidades em 10 silos entre 0 e 1: de 0 a 0,1, 0,1 a 0,2, …, 0,9 a 1. Os dados que utilizei são o conjunto de dados Titanic de Kaggle, onde a etiqueta a prever é uma variável binária Survived.

Vou traçar as curvas de calibração para dois modelos – um para regressão logística, e outro para floresta aleatória. Ambos os modelos produzem probabilidades de classe em Survived com base em duas características Age e Sex.

+----+------+--------+| Age| Sex|Survived|+----+------+--------+|22.0| male| 0||38.0|female| 1||26.0|female| 1|+----+------+--------+

Pré-processamento

Antes de treinar os meus modelos, preenchi os valores em falta em Age com a sua média e também transformei Sex numa variável numérica com valores 0 e 1.

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn import preprocessingfrom sklearn import model_selectiontitanic = pd.read_csv('train.csv')fitted_age_imputer = preprocessing.Imputer(axis=1).fit(titanic.values)titanic = fitted_age_imputer.transform( titanic.values.reshape(1, -1) ).transpose()titanic = np.where(titanic.Sex == 'female', 1, 0)

Então, dividi os dados em formação e validação definidos por uma divisão 80/20.

from sklearn import model_selectionfeature_cols = feature_train, feature_test, label_train, label_test = ( model_selection.train_test_split( titanic, titanic.Survived, test_size=0.2, random_state=1) )

Formação e previsão

P>Posso agora treinar um modelo de regressão logística no meu conjunto de formação e prever no conjunto de validação.

from sklearn.linear_model import LogisticRegressionlogreg_model = LogisticRegression().fit(X=feature_train,y=label_train)logreg_prediction = logreg_model.predict_proba(feature_test)

Simplesmente, treinar um modelo florestal aleatório e prever no conjunto de validação.

from sklearn.ensemble import RandomForestClassifierrf_model = RandomForestClassifier(random_state=1234).fit(X=feature_train, y=label_train)rf_prediction = rf_model.predict_proba(feature_test)

A probabilidade de classe positiva é devolvida pelos modelos na segunda coluna (index=1):

logreg_prediction

array(, , , , ])

/div>

Plotagem de calibração

Após ter as probabilidades de classe e as etiquetas, posso calcular as caixas para um gráfico de calibração. Aqui utilizo sklearn.calibration.calibration_curve que devolve o (x,y) coordenadas das caixas no gráfico de calibração.

from sklearn.calibration import calibration_curvelogreg_y, logreg_x = calibration_curve(label_test, logreg_prediction, n_bins=10)

), array()]

Next, calculo as coordenadas para os contentores do modelo de floresta aleatória.

rf_y, rf_x = calibration_curve(label_test, rf_prediction, n_bins=10)

%matplotlib inlineimport matplotlib.pyplot as pltimport matplotlib.lines as mlinesimport matplotlib.transforms as mtransformsfig, ax = plt.subplots()# only these two lines are calibration curvesplt.plot(logreg_x,logreg_y, marker='o', linewidth=1, label='logreg')plt.plot(rf_x, rf_y, marker='o', linewidth=1, label='rf')# reference line, legends, and axis labelsline = mlines.Line2D(, , color='black')transform = ax.transAxesline.set_transform(transform)ax.add_line(line)fig.suptitle('Calibration plot for Titanic data')ax.set_xlabel('Predicted probability')ax.set_ylabel('True probability in each bin')plt.legend()plt.show()

totais de caixas e discriminação

Existem apenas 4 caixas não vazias para regressão logística quando pedi 10 caixas. Será isto uma coisa má? Vamos utilizar uma função que retirei do código fonte de sklearn.calibration.calibration_curve para descobrir quais são os contentores em falta.

def bin_total(y_true, y_prob, n_bins): bins = np.linspace(0., 1. + 1e-8, n_bins + 1) # In sklearn.calibration.calibration_curve, # the last value in the array is always 0. binids = np.digitize(y_prob, bins) - 1 return np.bincount(binids, minlength=len(bins))bin_total(label_test, logreg_prediction, n_bins=10)

array(, dtype=int64)

Os contentores em falta têm valores médios de 5%, 35%, 45%, 55%, 85%, e 95%. De facto, ter totais baixos ou caixas vazias nas caixas intermédias (30-60%) pode na realidade ser uma coisa boa – quero que as minhas previsões evitem essas caixas intermédias e se tornem discriminatórias.

Discriminação é um conceito que vai lado a lado com a calibração em problemas de classificação. Por vezes vem antes da calibração se o objectivo na construção de um modelo é tomar decisões automáticas em vez de fornecer estimativas estatísticas. Imagine o cenário onde tenho dois modelos meteorológicos e vivo em Podunk, Nevada, onde 10% (36 dias por ano) dos dias são de chuva:

• modelo A diz sempre que há 10% de probabilidade de chuva, independentemente do dia em que seja.

li>modelo B diz que vai chover todos os dias em Junho (100%), e nunca chove nos outros 11 meses (0%).

modelo A está perfeitamente calibrado. Há apenas um contentor – o contentor de 10% – e a verdadeira probabilidade é de 10%. O modelo B, contudo, está ligeiramente fora de calibração porque haverá 30 dias no contentor de 100%, mas também 6 dias de chuva no contentor de 0%. Mas o modelo B é claramente mais útil se eu estiver a fazer planos de caminhadas de fim-de-semana. O modelo B é mais discriminativo do que A, porque é mais fácil tomar decisões (caminhadas/sem caminhadas) com base nos resultados do modelo B.

Discriminação é frequentemente verificada com as curvas características de funcionamento do receptor, ou curvas ROC, mas isso é um tópico para outro post.

Validação cruzada?

Se não me interessa a discriminação e só quero uma boa calibração, então a regressão logística (azul) parece fazer melhor do que a floresta aleatória (laranja). Será realmente esse o caso? Em particular, se eu olhar para o número de pontos nos contentores para floresta aleatória,

bin_total(label_test, rf_prediction, n_bins=10)

array(, dtype=int64)

Suspeito que o problema pode ser que alguns contentores tenham muito poucos pontos de dados. Coloquei 200 pontos em 10 contentores, por isso alguns contentores só receberão alguns, por isso a parcela de calibração sofre porque uma classificação errada num pequeno contentor altera grandemente a proporção.

Apenas 20% dos meus dados foram utilizados na parcela anterior, por isso talvez eu possa utilizar mais. Para fazer uso de todos os meus dados no teste de calibração entre diferentes modelos, pensei poder roubar a ideia da validação cruzada. Se eu dividir os meus dados em 5 dobras para validação cruzada, então cada dobra será usada como conjunto de validação uma vez. Portanto, posso concatenar as probabilidades previstas nas 5 dobras e fazer um gráfico de calibração a partir delas. O resultado de um gráfico de calibragem de 5 dobras é o seguinte gráfico. O código pode ser encontrado na última secção do caderno de notas Jupyter.

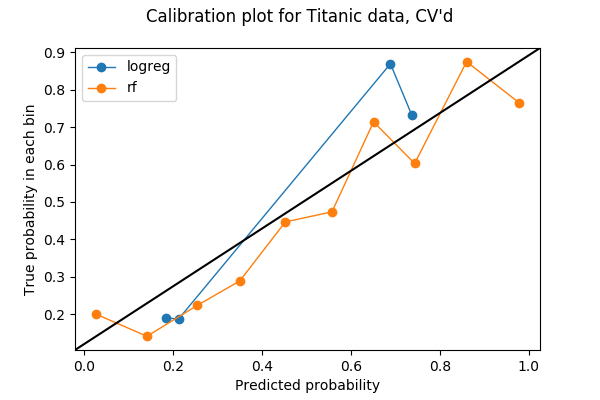
Cada caixa tem agora mais pontos:

array(, dtype=int64)

e penso ser seguro dizer que, neste exemplo, a floresta aleatória é melhor calibrada do que a regressão logística.

***

Nate Silver tem um grande exemplo de calibração meteorológica no livro O Sinal e o Ruído, onde estudou as previsões de três fontes – o Serviço Meteorológico Nacional, o Canal Meteorológico, e os canais de notícias locais – no Capítulo 4, Durante Anos Tens Estás a Dizer-nos que a Chuva é Verde. Ele concluiu que a maioria dos canais de notícias locais são mal calibrados e estão “molhados”. É uma jóia, e eu recomendo que pegue no livro se conseguir pôr a mão nele.

A primeira vez aprendi sobre calibração através do meu colega Kevin em 2016, quando discutimos várias métricas sobre modelos de classificação. Sem ele, provavelmente levarei mais um ou dois anos antes de me aperceber da importância da calibração, e muito mais tarde antes de escrever este post.