Encontrar uma função exponencial dado o seu gráfico – Funções Exponenciais

O que são funções exponenciais?

Antes de começarmos a lidar com funções exponenciais e com gráficos de funções exponenciais, vejamos primeiro a fórmula geral e a teoria por detrás das funções exponenciais.

Below é uma das formas mais gerais de um gráfico exponencial:

A equação da função exponencial deste gráfico é y=2xy=2^xy=2x, e é o gráfico exponencial mais simples que podemos fazer. Se está a pensar como seria y=1xy=1^xy=1x, aqui está o seu gráfico exponencial:

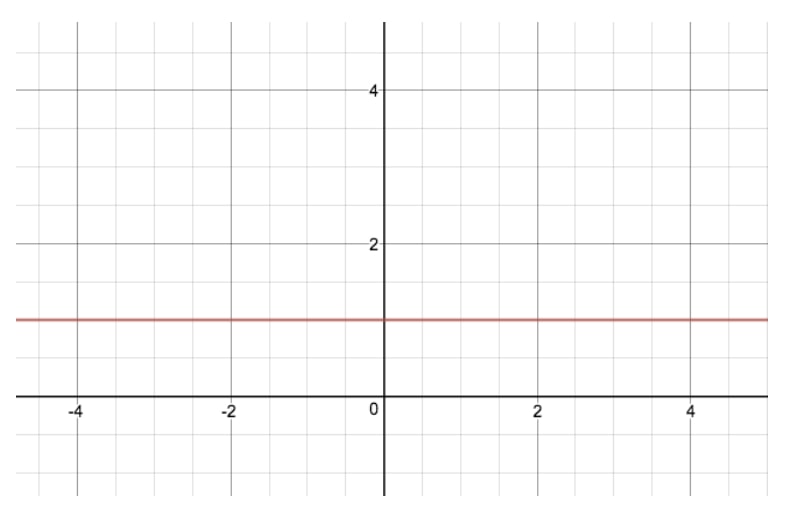
Agora, quanto à razão pela qual os gráficos de y=2xy=2^xy=2x e y=1xy=1^xy=1x são tão diferentes, a melhor maneira de compreender a teoria por detrás das funções exponenciais é dar uma vista de olhos a algumas tabelas.

Acima podem ver-se três tabelas para três “valores base” diferentes – 1, 2 e 3 – todos os quais estão ao poder de x. Como se pode ver, para funções exponenciais com um “valor base” de 1, o valor de y permanece constante em 1, porque 1 para a potência de qualquer coisa é apenas 1. É por isso que o gráfico acima de y=1xy=1^xy=1x é apenas uma linha recta. No caso de y=2xy=2^xy=2x e y=3xy=3^xy=3x (não ilustrado), por outro lado, vemos uma curva cada vez mais acentuada para o nosso gráfico. Isto porque à medida que x aumenta, o valor de y aumenta para um valor cada vez maior, ou aquilo a que chamamos “exponencialmente”.

Agora que temos uma ideia do aspecto das equações exponenciais num gráfico, vamos dar a fórmula geral para funções exponenciais:

y=abd(x-c)+ky=ab^{d(x-c)}+ky=abd(x-c)+k

A fórmula acima é um pouco mais complicada do que as funções anteriores com que provavelmente trabalhou, por isso vamos definir todas as variáveis.

y – o valor no eixo y

a – o factor de estiramento ou compressão vertical

b – o valor de base

x – o valor no eixo x

c – o factor de translação horizontal

d – o factor de estiramento ou compressão horizontal

k – o factor de translação vertical

nesta lição, só vamos rever funções exponenciais muito básicas, por isso não precisa de se preocupar com algumas das variáveis acima. Mas, para que tenha acesso a toda a informação de que necessita sobre funções exponenciais e como fazer o gráfico de funções exponenciais, vamos delinear o que a alteração de cada uma destas variáveis faz ao gráfico de uma equação exponencial.

1) Variável “a”

Vamos comparar o gráfico de y=2xy=2^xy=2x com outra equação exponencial onde modificamos “a”, dando-nos y=(-4)2xy=(-4)2^xy=(-4)2x

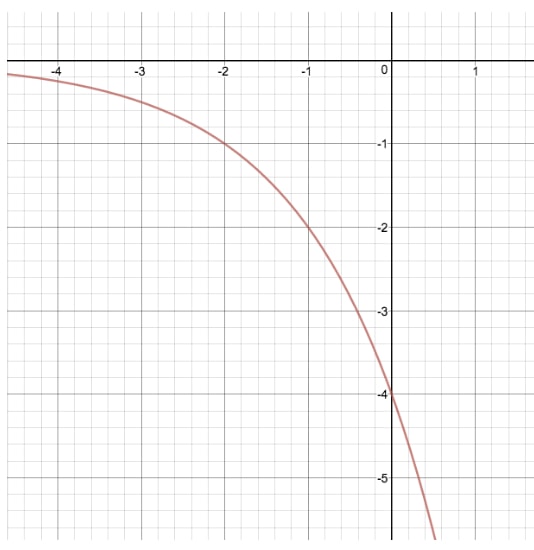
Fazendo esta transformação, temos tanto “esticado” como “reflectido” o gráfico original de y=2xy=2^xy=2x pelos seus valores de y. A fim de encontrar “a” olhando para o gráfico, o mais importante a notar é que quando x=0 e não temos um valor para “k”, o y-intercepção do nosso gráfico será sempre igual a “a”.

2)Variável “b”

p> Tão conhecido como o “valor base” este é simplesmente o número que tem o expoente ligado a ele. A sua descoberta envolve álgebra, que será discutida mais adiante neste artigo.

Variável “c”

P>Vamos comparar o gráfico de y=2xy=2^xy=2x com outra equação exponencial onde modificamos “c”, dando-nos y=2(x-2)y=2^{(x-2)}y=2(x-2)

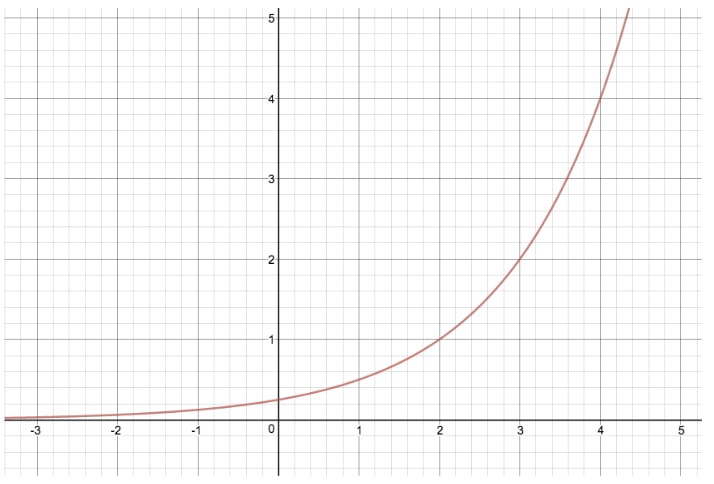
Fazendo esta transformação, deslocámos todo o gráfico para as duas unidades correctas. Se “c” fosse igual a -2, teríamos deslocado todo o gráfico para a esquerda, duas unidades.

Variável “d”

Vamos comparar o gráfico de y=2xy=2^xy=2x com outra equação exponencial onde modificamos “d”, dando-nos y=24xy=2^{4x}y=24x

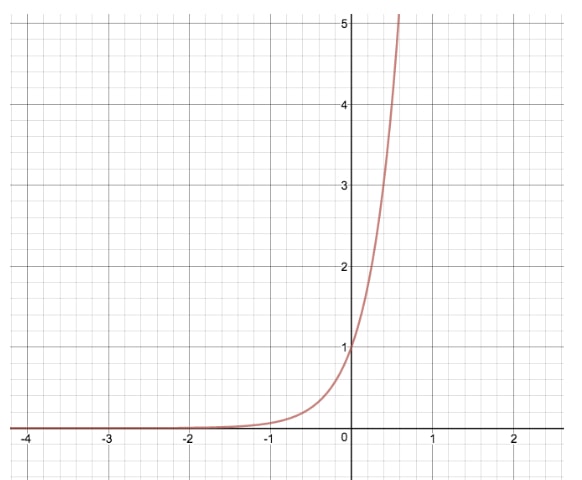
Fazendo esta transformação, esticámos o gráfico original de y=2xy=2^xy=2x pelos seus valores x, semelhante a como a variável “a” modifica a função pelos seus valores y. Se “d” fosse negativo neste exemplo, a função exponencial seria submetida a uma reflexão horizontal em oposição à reflexão vertical vista com “a”.

Variável “k”

Vamos comparar o gráfico de y=2xy=2^xy=2x com outra equação exponencial onde modificamos “k”, dando-nos y=2x+2y=2^x+2y=2x+2

/div>

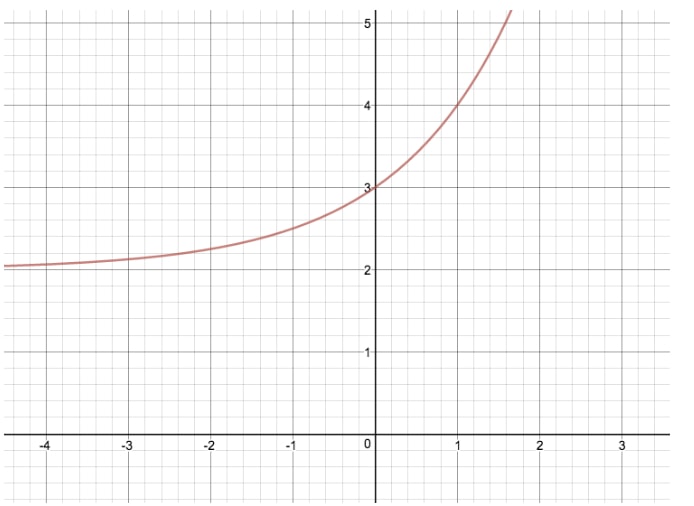
Fazendo esta transformação, traduzimos o gráfico original de y=2xy=2^xy=2x acima de duas unidades. Se “k” fosse negativo neste exemplo, a função exponencial teria sido traduzida para baixo duas unidades. O “k” é uma variável particularmente importante, pois é também igual ao que chamamos de assímptota horizontal! Uma assímptota é um valor para x ou y que uma função se aproxima, mas nunca é de facto igual.

Toma por exemplo a função y=2xy=2^xy=2x: para esta função exponencial, k=0, e portanto a “assímptota horizontal” é igual a 0. Isto faz sentido, porque independentemente do valor que colocarmos para x, nunca conseguiremos que y seja igual a 0. Para a nossa outra função y=2x+2y=2^x+2y=2x+2, k=2, e portanto a “assímptota horizontal” é igual a 2. Não há valor para x que possamos usar para fazer y=2.

E estas são todas as variáveis! Mais uma vez, várias destas são mais complicadas do que outras, pelo que levará tempo a habituarmo-nos a trabalhar com todas elas e a habituarmo-nos a encontrá-las. Para ver melhor as funções exponenciais, e para se familiarizar com a equação geral acima, visite este excelente site de calculadora gráfica aqui. Leve o seu tempo a brincar com as variáveis, e obtenha uma melhor percepção de como a alteração de cada uma das variáveis afecta a natureza da função.

Agora, vamos ao que interessa. Dado um gráfico de funções exponenciais, como podemos encontrar a equação exponencial?

Como encontrar funções exponenciais

Encontrar a equação de funções exponenciais é muitas vezes um processo de múltiplos passos, e cada problema é diferente com base na informação e no tipo de gráfico que nos é dado. Dado o gráfico de funções exponenciais, precisamos de ser capazes de tirar alguma informação do próprio gráfico, e depois resolver para o material que não somos capazes de tirar directamente do gráfico. Abaixo está uma lista de todas as variáveis que podemos ter de procurar, e como as encontrar normalmente:

a – resolver para ele usando álgebra, ou será dado

b – resolver para ele usando álgebra, ou será dado

c – deixar x = 0 e imaginar que “c” não está lá, o valor de y será igual ao y-intercepção; agora conte quantas unidades o valor de y para o intercepção y é do eixo y, e isto será igual a “c”

d – resolver para ele usando álgebra

k – igual ao valor da assímptota horizontal

Obviamente, estes são apenas os passos gerais que precisa de dar para encontrar a equação da função exponencial. A melhor maneira de aprender a fazer isto é tentar alguns problemas práticos!

Exemplos de funções exponenciais:

Agora vamos tentar alguns exemplos a fim de pôr em prática toda a teoria que cobrimos. Com a prática, será capaz de encontrar funções exponenciais com facilidade!

Exemplo 1:

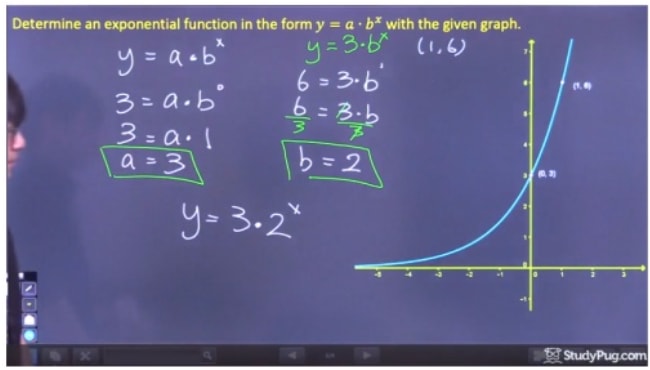
Determinar a função exponencial na forma y=abxy=ab^xy=abx do gráfico dado.

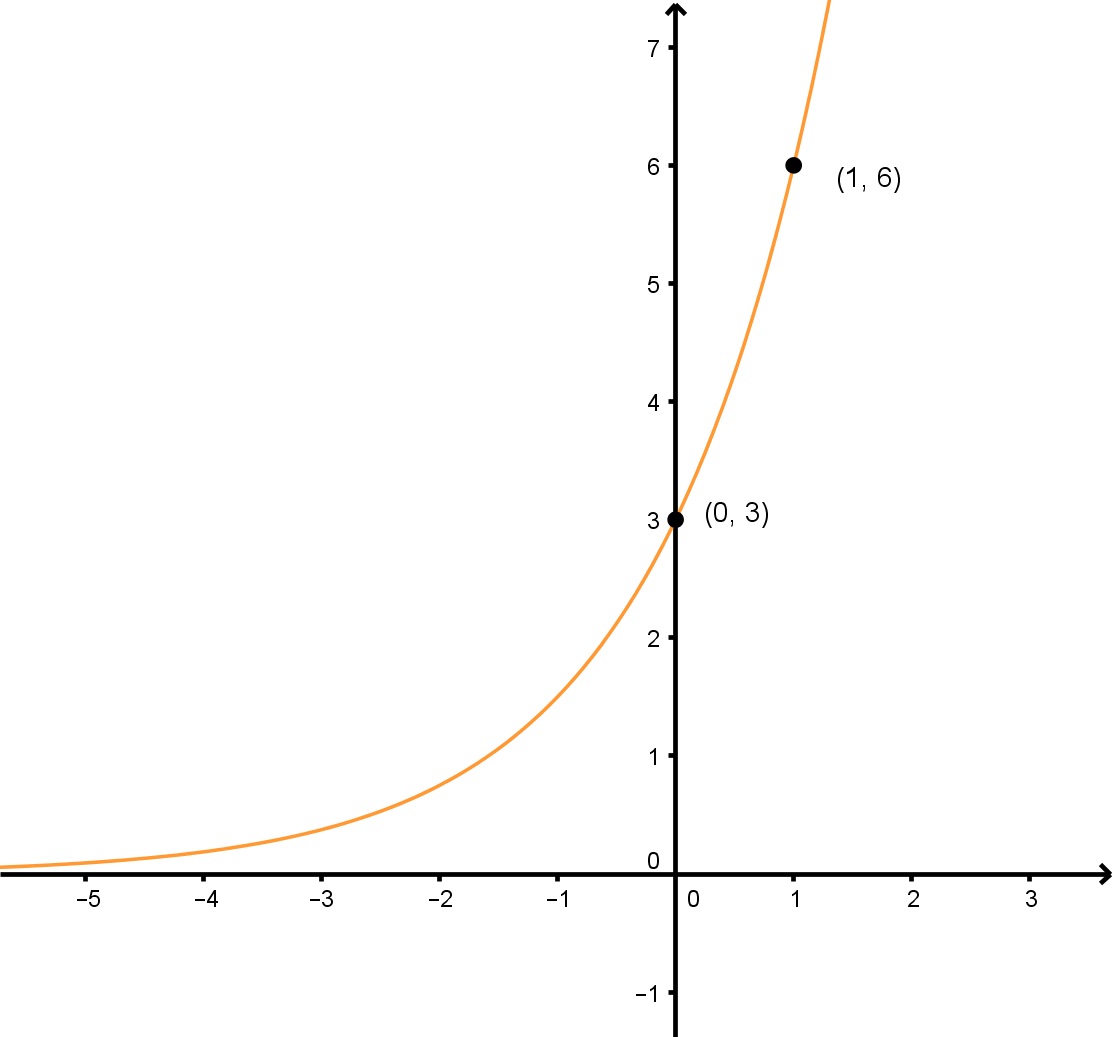
Para resolver este problema, vamos precisar de encontrar as variáveis “a” e “b”. Também vamos ter de resolver estas duas algébricas, pois não as podemos determinar a partir do próprio gráfico de função exponencial.

P>Passo 1: Resolver para “a”

Para resolver para “a”, devemos escolher um ponto no gráfico onde possamos eliminar bx porque ainda não sabemos “b”, e por isso devemos escolher o intercepção y (0,3). Uma vez que b0 é igual a 1, podemos encontrar que a=3. Como atalho, uma vez que não’ temos um valor para k, a é apenas igual ao intercepção y desta equação.

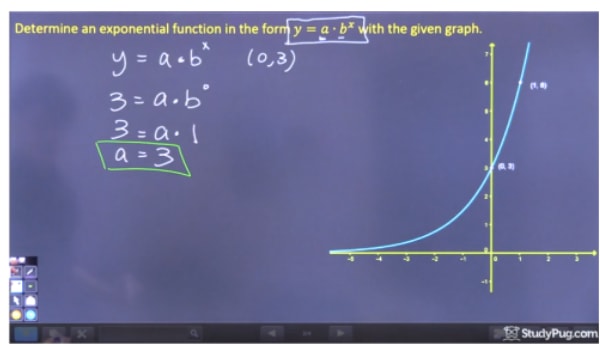
Step 2: Resolver para “b”

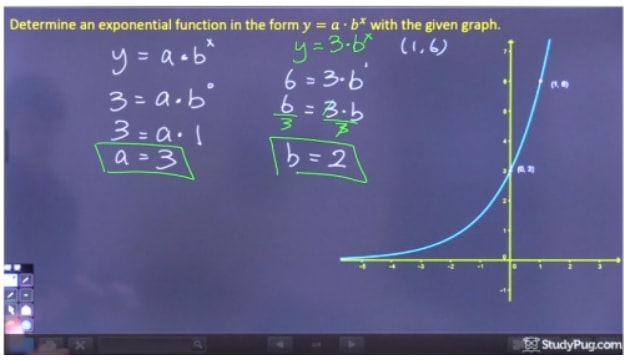
Step 3: Escreva a Equação Final

Exemplo 2:

determinar a função exponencial na forma y=a2dx+ky=a2^{dx}+ky=a2dx+k do gráfico dado.

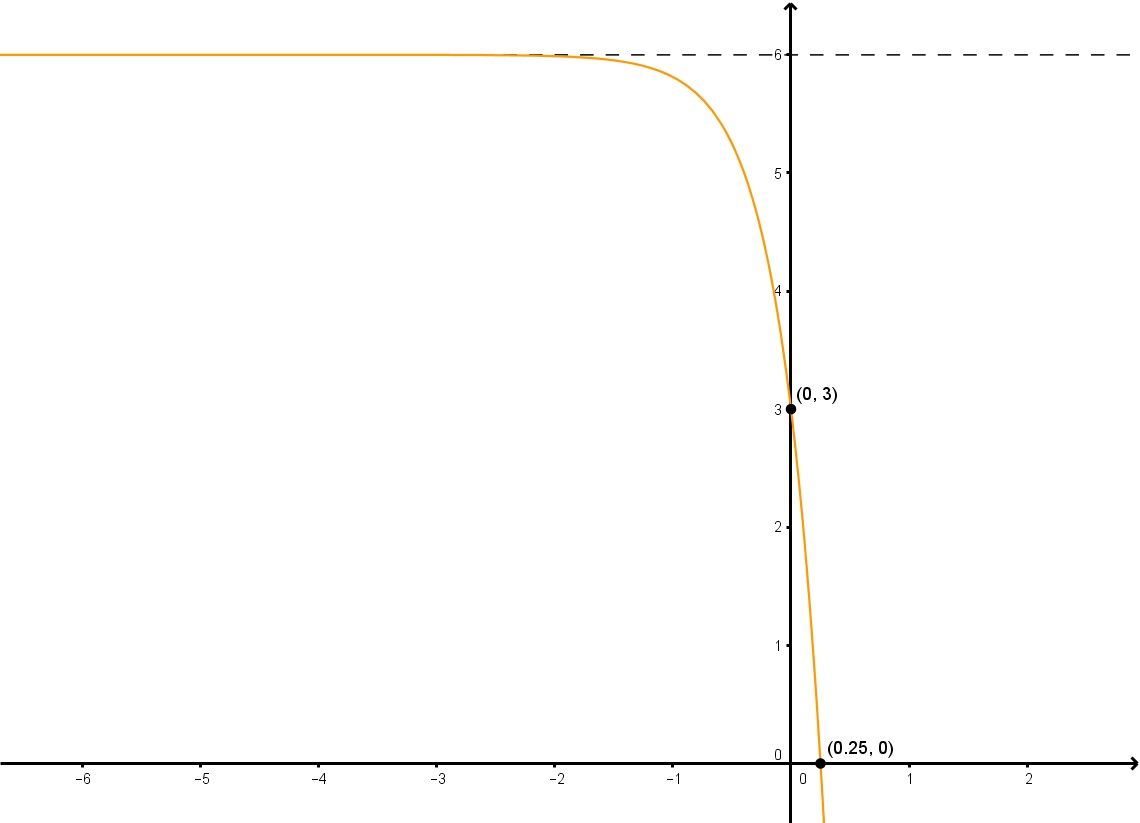
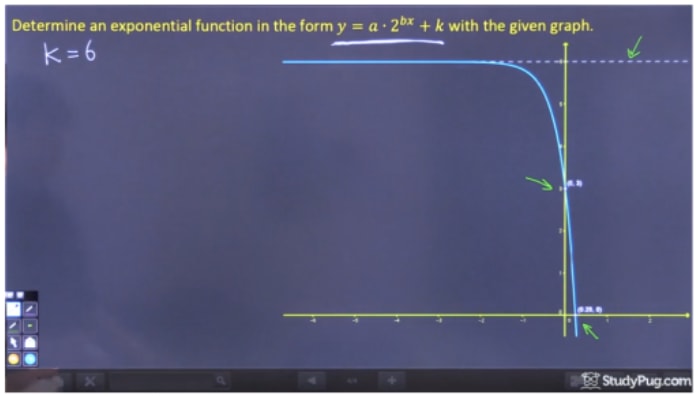
Step 1: Encontrar “k” no Gráfico

Para encontrar “k”, tudo o que precisamos de fazer é encontrar a assímptota horizontal, que é claramente y=6. Portanto, k=6.

Step 2: Resolver para “a”

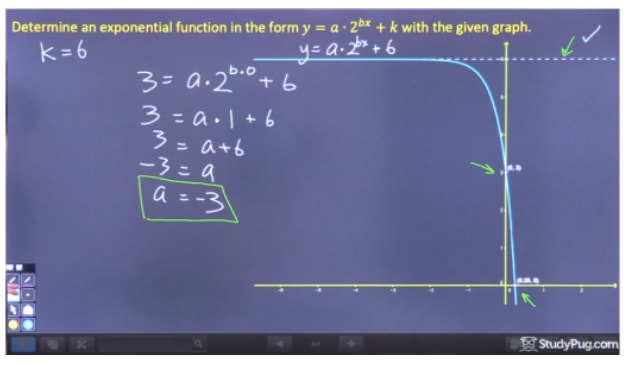
Step 3: Resolver para “b”

Step 4: Escreva a Equação Final

E é tudo para funções exponenciais! Mais uma vez, estas funções são um pouco mais complexas do que as equações para linhas ou parábolas, por isso não se esqueça de fazer muitos problemas práticos para se apoderar das novas variáveis e técnicas. Com mais prática, em breve as equações exponenciais e os gráficos de funções exponenciais não serão problema algum!