Factorial

O que é Factorial?

O Factorial (denotado ou representado como n!) para um número positivo ou inteiro (que é denotado por n) é o produto de todos os números positivos anteriores ou equivalentes a n (o inteiro positivo). A função factorial pode ser encontrada em várias áreas da matemática, incluindo álgebra, análise matemática, e combinatórias.

Início no século XII, foram utilizados factores para contar permutações. A notação para um factorial (n!) foi introduzida no início do século XIX por Christian Kramp, um matemático francês.

A fórmula factorial pode ser vista abaixo:

Factorial – Fórmula

Definindo o Factorial

A função de um Factorial é definida pelo produto de todos os inteiros positivos anteriores e/ou igual a n, ou seja:

n! = 1 ∙ 2 ∙ 3 ∙∙∙ (n-2) ∙ (n -1) ∙ n,

quando se olha para valores ou inteiros maiores ou iguais a 1. Pode então ser escrito como:

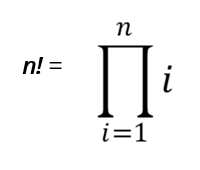
A equação acima é escrita de acordo com a notação de produto pi, e resulta na relação recorrente vista abaixo:

n! = n ∙ (n – 1) !.

Alguns exemplos da notação podem ser vistos abaixo:

• 4! = 4 ∙ 3!
• 7! = 7 ∙ 6!
• 80! = 80 ∙ 79!, etc.

Tabela Factorial

A tabela abaixo dá uma visão geral dos factores para números inteiros entre 0 e 10:

Tabela Factorial

Factorial de 0 (Zero)

É amplamente conhecido que o Factorial de 0 é igual a 1 (um). Pode ser denotado como:

0! = 1

Há várias razões para justificar a notação e definição acima estipuladas. Em primeiro lugar, a definição permite uma expressão compacta de um número considerável de fórmulas, incluindo a função exponencial e a definição cria uma extensão da relação de recorrência a 0,

Além disso, onde n = 0, a definição do seu factorial (n!) engloba o produto sem números, o que significa que é equivalente à identidade multiplicativa em termos mais amplos.

Além disso, a definição do factorial zero inclui apenas uma permutação de zero ou nenhum objecto. Finalmente, a definição valida também um número de identidades em combinatórias.

Definições a notar em relação ao Factorial Zero

• Combinatorics: Uma área em matemática que se concentra na contagem.
• Permutação: Em matemática, permutação refere-se à disposição dos membros de um conjunto numa ordem ou sequência linear.
• Relação de recorrência: Relação de recorrência, em matemática, refere-se a uma equação que define uma sequência ou vasto conjunto de valores, recursivamente. Recurrência significa definir algo em termos próprios.

Várias Aplicações para a Função Factorial

A função factorial pode ser encontrada em vários campos da matemática. Em primeiro lugar, existem n! formas distintas de organizar n objectos específicos numa sequência. Além disso, os factores podem ser utilizados para explicar a ignorância ou o desrespeito da ordenação numa fórmula, servindo como denominador.

Factoriais também ocorrem em álgebra através do teorema binomial e em cálculo, onde ocorrem nos denominadores da fórmula de Taylor. Além disso, um factorial pode ser encontrado nas teorias da probabilidade e dos números e pode ser utilizado para permitir a manipulação de expressões.

Outras sequências semelhantes ao Factorial

Em matemática, há um número de sequências que são comparáveis ao factorial. Elas incluem:

• Duplos Factoriais, que são utilizados para simplificar integrais trigonométricos.
• Multi-factoriais, que podem ser denotados com múltiplos pontos de exclamação.
• Primorials, que implicam obter o produto dos números primos, que são inferiores ou iguais a n.
• Superfactoriais, que são definidos como o produto dos primeiros n factorials.
• Hiper-factoriais, que são o resultado da multiplicação de um número de valores consecutivos que vão de 1 a n.

Recursos Adicionais

CFI é o fornecedor oficial da Banca Comercial global & Analista de Crédito (CBCA)™CBCA™ CertificationThe Commercial Banking & Credit Analyst (CBCA)™ acreditação é um padrão global para analistas de crédito que cobre finanças, contabilidade, análise de crédito, análise de fluxo de caixa, modelação de pactos, reembolso de empréstimos, e muito mais. programa de certificação, concebido para ajudar qualquer pessoa a tornar-se um analista financeiro de classe mundial. Para continuar a avançar na sua carreira, os recursos adicionais de CFI abaixo serão úteis:

• MatrixCorrelation MatrixUma matriz de correlação é simplesmente uma tabela que exibe os coeficientes de correlação para diferentes variáveis. A matriz retrata a correlação entre todos os pares de valores possíveis de uma tabela. É uma ferramenta poderosa para resumir um grande conjunto de dados e para identificar e visualizar padrões nos dados fornecidos.

Matemática financeiraMatemática financeiraMatemática financeira descreve a aplicação da matemática e da modelação matemática para resolver problemas financeiros. é por vezes referida como

• QuantsQuantsQuantsOs analistas quantitativos (também chamados “quants”) são profissionais especializados na concepção, desenvolvimento e implementação de algoritmos e modelos matemáticos ou estatísticos destinados a resolver problemas financeiros complexos. No seu trabalho, os analistas quantitativos aplicam uma mistura de técnicas e conhecimentos

li>Distribuição de AmostragemDistribuição de AmostragemUma distribuição de amostragem refere-se a uma distribuição de probabilidade de uma estatística que provém da escolha de amostras aleatórias de uma dada população