Fórmulas úteis de Matemática do SAT
Uma das primeiras coisas a fazer ao estudar para a secção de Matemática do SAT é memorizar as fórmulas. Se não tiver a certeza por onde começar, esta lista irá ajudar.
Aqui estão 9 fórmulas de matemática SAT que o ajudarão ao fazer o teste. Use esta lista como um início.
Aprenda a preparar-se para testes padronizados com os nossos cursos de preparação para o SAT e ACT, hoje mesmo, durante todo o ano.
p>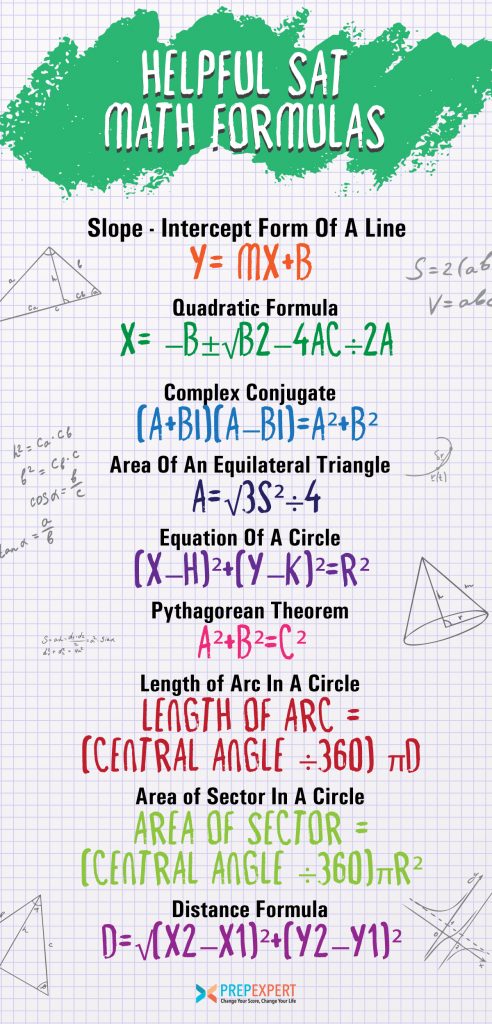
Forma de Intercepção da Linha A
y=mx+b
“m” representa a inclinação da equação, “b” representa o valor y do intercepção y. Por exemplo, se tivermos a equação y=3x+5, então a inclinação é ‘3’ e o intercepção y é (0,5).
Fórmula quadrática
x=-b±√b2-4ac÷2a
Com esta fórmula, é possível encontrar as raízes de uma equação quadrática se esta não for facilmente factorável. No entanto, o quadrático tem de ter a forma de y=ax2+bx+c.
Nesse ponto, ligue os coeficientes e constantes à fórmula. Lembre-se, devido ao ± no numerador, terá duas respostas separadas.
Conjugador Complexo
(a+bi)(a-bi)=a²+b²
Testes de Matemática do SAT terão, pelo menos, uma pergunta que requer a manipulação de números imaginários. A fórmula conjugada complexa permite cancelar a parte imaginária de um número complexo. Como resultado, ficará com um número real.
Área de um Triângulo Equilateral
A=√3s²÷4
A fórmula da área de um triângulo regular é normalmente fornecida na folha de referência do teste, mas é necessário conhecer a altura do triângulo. Por vezes não lhe será fornecida a altura e terá de a calcular.
A boa notícia é que pode calcular a área de um triângulo equilátero ligando o comprimento de um dos seus lados a esta fórmula. Pode saltar a exigência de altura!
Equação de um círculo
(x-h)²+(y-k)²=r²
Normalmente, uma pergunta de Matemática de SAT será necessária utilizando a equação de um círculo. Nesta equação, as variáveis h e k representam a coordenada para o centro do círculo e r
representa o raio do círculo.
Teorema de Pitágoras
a²+b²=c²
O Teorema de Pitágoras aplica-se a triângulos rectos regulares. A e b são as pernas do triângulo, e c é a hipotenusa.
Comprimento do arco em círculo
comprimento do arco = (ângulo central ÷360) πd
P>Perguntas geométricas não são frequentes na secção de Matemática do SAT, mas provavelmente ainda receberá uma pergunta sobre arcos ou sectores em círculo. Um arco é um comprimento entre dois pontos de um círculo.
São normalmente medidos através da extensão de dois raios do centro do círculo com um ângulo formado entre eles. Pode-se usar a medida do grau desse arco como uma fracção de 360 e depois multiplicá-lo pela equação da circunferência para encontrar o comprimento do arco.
Área do sector num círculo
área do sector = (ângulo central ÷360)πr²
Não é diferente de um arco, o sector de um círculo é a área entre dois raios que se estendem a partir do centro. Visualmente, pensem nisto como uma fatia de torta basicamente. Mais uma vez, multiplique a medida de grau como uma fracção de 360 e depois multiplique pela equação da área de um círculo para encontrar a área do sector.
Fórmula da distância
d=√(x2-x1)²+(y2-y1)²
A fórmula da distância é fantástica para determinar rapidamente a distância entre dois pontos. Para a utilizar, basta pegar nos valores das coordenadas e ligá-los para encontrar a distância. e não se esqueça de aplicar os quadrados e a raiz quadrada no passo certo.
Para mais estratégias de teste, admissões universitárias, e dicas de aplicação de bolsas de estudo inscreva-se na nossa turma GRATUITA a acontecer agora mesmo!