Horizontal Stretch -Propriedades, Gráfico, & Exemplos

P>Pode já ter encontrado gráficos que se assemelham mas partilham larguras diferentes. Estas funções podem ter sido estiradas horizontalmente usando uma função de base. Os alongamentos horizontais estão entre as técnicas de transformação mais aplicadas quando se usam funções gráficas, por isso é melhor compreender a sua definição.

Extensões horizontais acontecem quando um gráfico de base é alargado ao longo do eixo x e afastado do eixo y.

Aprender como podemos esticar os gráficos horizontalmente pode ajudar-nos a compreender a família de gráficos de funções. Também podemos aprender a acelerar a criação de gráficos de novas funções com base nos factores de escala aplicados.

Não deixe de rever os seus conhecimentos sobre funções parentais, traduções e alongamentos verticais antes de passar à secção seguinte.

• Compreender as funções parentais comuns que possamos encontrar.
• Refresca os seus conhecimentos sobre transformações verticais e horizontais.
• Reveja como aplicamos alongamentos verticais.

Estes artigos ligados podem ajudá-lo a refrescar os seus conhecimentos, e quando estiver pronto, vamos avançar e aprender mais sobre estiramentos horizontais.

O que é um estiramento horizontal?

Podemos aplicar o estiramento horizontal a uma função multiplicando os seus valores de entrada por um factor de escala, a, onde 0 < 1/a < 1. O que significa isto para funções tais como f(x)? Quando 1/a é multiplicado por x, o gráfico de f(x) estende-se horizontalmente por um factor de escala de a.

Vejamos como f(x) = x2 será afectado por um factor de escala de 1/2 e 1/3.

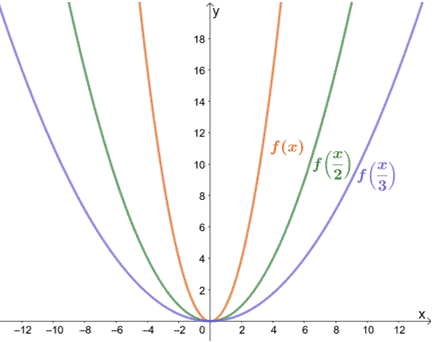
Como esperávamos, o gráfico estica-se por um factor de 2 e 3. Notar como os valores y permanecem os mesmos? Isto é verdade para todos os alongamentos horizontais. O gráfico só se afasta do eixo y quando esticamos horizontalmente um gráfico.

Estiramento horizontal em outras funções exibirá propriedades semelhantes. Digamos que temos f(x) = |x|, se o gráfico desta função deve ser esticado horizontalmente para atingir g(x), a expressão da nova função pode ser expressa como |1/3 ∙ x| = |x/3|.

Por que não comparamos alguns valores de ambas as funções?

x	-2	-1	0	1	2
f(x) = |x|	2	1	0	1	2

Esperamos também todos os seus x-coordenadas para aumentar em 3. Quando o fizermos, os valores de saída permanecerão os mesmos.

x	-6	-3	0	3	6
g(x) = |x/3|	2	1	0	1	2

O que significa isto para as coordenadas do gráfico da nova função? Se a função f(x) passar (m, n) e for esticada horizontalmente por um factor de 1/a, a nova função passará (am, n).

Como esticar horizontalmente uma função?

Agora de aprendermos sobre estiramentos horizontais e como estes afectam uma função base, é altura de os aplicarmos nos gráficos das funções. Antes de começarmos a esticar as funções horizontalmente por um determinado factor, lembremo-nos destes ponteiros para esticar os gráficos mais rapidamente na horizontal:

• Apenas esticar a base do gráfico horizontalmente para que as coordenadas y permaneçam na mesma posição.
• Li>Desde que as coordenadas y permaneçam as mesmas, o conceito y também permanece o mesmo.

Li>Certifique-se de verificar pontos críticos no gráfico, tais como as suas intercepções, pontos máximos, e mais.

• Ver se os pontos de coordenadas também são escalados correctamente.

P>Vejamos a tabela de valores mostrada na secção anterior para fazer o gráfico tanto y = |x| como y = |x/3| para visualizar os efeitos de um estiramento horizontal num gráfico.

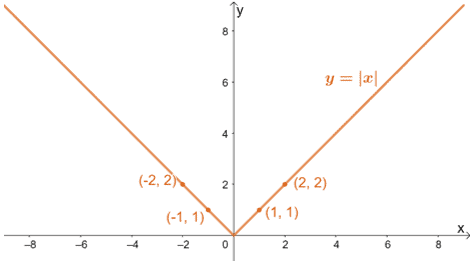
Como discutimos, esperamos que os gráficos estiquem ao longo da base com os valores para y permanecendo constantes.

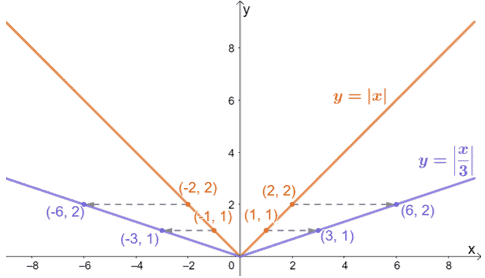
Para alcançar y = |x/3|, esticamos a função principal y = |x| por um factor de 3. O gráfico mostrado acima confirma isto, e podemos aplicar o mesmo processo ao esticar horizontalmente os gráficos de outras funções.

Pronto para esticar mais funções e aplicar esticamentos horizontais? Vamos resumir o que aprendemos até agora antes de tentarmos mais questões.

Resumo da definição e propriedades de estiramento horizontal

Aqui estão algumas indicações importantes a lembrar ao responder a problemas e funções gráficas que envolvam estiramentos horizontais:

• Só podemos esticar horizontalmente um gráfico por um factor de 1/a quando o valor de entrada também é aumentado por a.
• Quando f(x) é esticado horizontalmente para f(ax), multiplique as coordenadas x por a.
• Retain the y-intercepts’ position.
• A função resultante terá o mesmo alcance mas pode ter um domínio diferente.
• Dado um ponto (m, n), ele torna-se (am, n) quando esticado horizontalmente.

Vamos sempre voltar a estes cinco-pontos quando em dúvida. Ser capaz de dominar a técnica de esticar horizontalmente os gráficos pode ajudar-nos a fazer gráficos de funções mais rapidamente e a compreender o seu comportamento.

Está pronto para testar os seus conhecimentos? Vamos em frente e experimentar alguns destes problemas!

Exemplo 1

A função, g(x), é obtida por estiramento horizontal f(x) = 8x por um factor de escala de 1/4. Qual das seguintes é a expressão correcta para g(x)?

a. g(x) = 32x
b. g(x) =16x
c. g(x) = 2x
d. g(x) =1/2 x

Solução

Lembrem-se que quando esticamos horizontalmente uma função por 1/a, dividimos o valor de entrada por a. Porque não aplicamos isto ao problema? Substituímos x por x/4 para encontrar a expressão para g(x).

g(x) = 8(x/4)

Simplificar a expressão levará a g(x) = 2x.

Exemplo 2

Escrever as expressões para g(x) e h(x) em termos de f(x) dadas as seguintes condições:

a. A função g(x) é o resultado de f(x) ser esticada horizontalmente por um factor de 1/5.
b. Quando esticamos horizontalmente g(x) por um factor de escala de 1/2, obtemos h(x).

Solução

P>P>Comecemos com g(x). Podemos esticar horizontalmente f(x) para obter g(x), pelo que dividimos o valor de entrada de f(x) por 5 para obter a expressão de g(x): f(x/5).

P>Agora que temos g(x), podemos encontrar a expressão para h(x). Dividimos o valor de entrada de g(x) por 2. Assim, temos:

h(x) = g(x/2)

= f(x/5 -1/2 )

= f(x/10)

Isto significa que em termos de f(x), g(x) = f(x/5) e h(x)= f(x/10).

Exemplo 3

A função, f(x), passa através do ponto (6, 4). Se f(x) é horizontalmente esticado por um factor de escala de 1/2, qual seria a nova coordenada-x do ponto?

Solução

Quando esticamos um gráfico horizontalmente, multiplicamos a x-coordenada da função base pelo denominador do factor de escala dado para encontrar o novo ponto ao longo da mesma y-coordenada.

Hence, temos (6, 4) → (2 ∙ 6, 4). A nova x-coordenada do ponto será (12, 4).

Exemplo 4

A tabela de valores para f(x) é mostrada abaixo. Se h(x) é o resultado de f(x) ser esticado horizontalmente por um factor de escala de 1/4, construa a sua tabela de valores e mantenha os valores da corrente de saída.

x	-3	-2	-1	0	1	2	3
f(x)	-6	-4	-2	0	2	4	6

Solução

Quando a função é esticada horizontalmente, multiplicamos os valores de entrada (para este caso, são os valores de x) pelo denominador do factor de escala dado.

Isto significa que (-2, -4) será transformado para (4∙ -2, -4) = (-8, -4). Aplicamos o mesmo processo para os restantes valores e temos a tabela de valores de h(x) como se mostra abaixo.

x	-12	-8	-4	0	4	8	12
h(x)	-6	-4	-2	0	2	4	6

Exemplo 5

Observar as funções mostradas abaixo. Qual é a relação entre f(x) e g(x)?

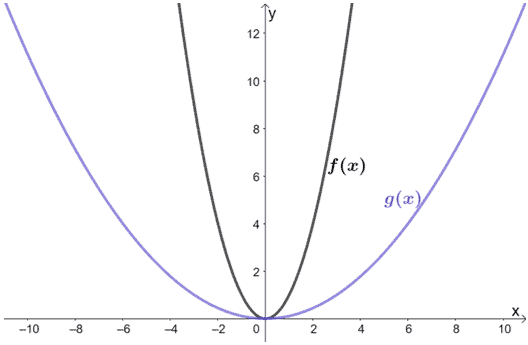
Solução

Apenas olhando para o gráfico, podemos ver que g(x) resulta de f(x) ser esticado horizontalmente. Porque não inspeccionamos alguns pontos de ambos os gráficos?

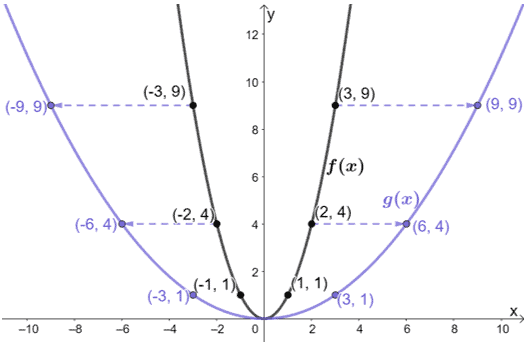
É o que acontece com os pontos:

• (-3, 9) → (-9, 9)
• (-2, 4) → (-6, 4)
• (-1, 1) → (-3, 1)
• (0, 0) → (0, 0)
• (1, 1) → (3, 1)
• (2, 4) → (6, 4)
• (3, 9) → (9, 9)

Notificação de como para cada caso: as coordenadas-x de g(x) são todas três vezes maiores do que f(x). Isto significa que o factor de escala utilizado para esticar f(x) é 1/3.

A função g(x) é o resultado de f(x) ser esticado horizontalmente por um factor de escala de 1/3.

Exemplo 6

A imagem abaixo mostra o gráfico de f(x). Gráfico g(x) utilizando o facto de ser o resultado de f(x) ser esticado horizontalmente por um factor de 1/2. Certifique-se de incluir os novos pontos críticos de g(x).

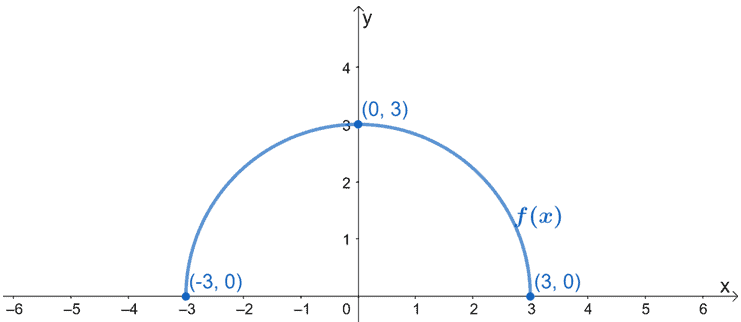
Solução

P>Vamos procurar primeiro os novos pontos críticos de g(x). Uma vez que f(x) será esticado horizontalmente, multiplicaremos as coordenadas x por 2. Assim, temos os seguintes pontos críticos:

• (-3, 0) → (-6, 0)
• (0, 3) → (0, 3)
• (3, 0) → (6, 0)

Plotar estes pontos e esticar o gráfico de f(x) por 3. Certifique-se de que as coordenadas y e o conceito y permanecem os mesmos.

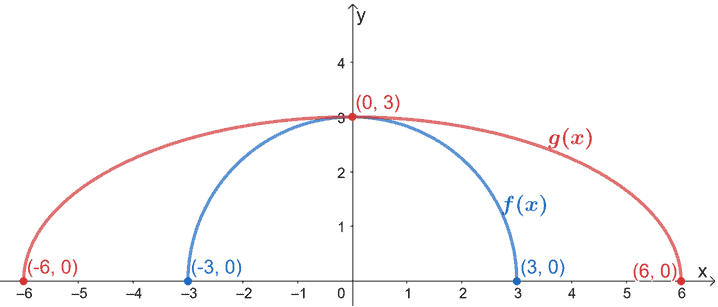
É assim que deve ser o gráfico resultante. Como g(x) é o resultado de f(x) ser esticado horizontalmente, esticamos o gráfico de f(x) por uma escala de 3.

Exemplo 7

Descreve as transformações feitas nas seguintes funções mostradas abaixo.

a.f(x) = x2 → g(x) = x2/9

b. m(x) = √x → n(x) = 3√(x/4)
c. p(x) = 3x – 1→ q(x) = 3x/4 – 2

Solução

se tiver notado que alguns podem não só exibir alongamentos horizontais, tem razão!

Cuidado que por vezes temos de aplicar diferentes técnicas de transformação para obtermos a expressão de uma determinada função.

Primeiro, comecemos por f(x) e g(x):

Para verificar o factor de escala aplicado no valor de entrada de f(x) para atingir g(x), vamos expressar g(x) como um quadrado perfeito: g(x) = (x/3)2 = (1/3 – x)2.

Expressão de g(x) em termos de f(x), temos g(x) = f(x/3). Assim, g(x) é o resultado de f(x) ser esticado horizontalmente por um factor de escala de 1/3.

Movendo-se para m(x) e n(x):

Vemos dois factores de escala aplicados a n(x): 3 sobre o valor de saída e 1/4 para o valor de entrada. Aplicando o que sabemos em estiramentos verticais e horizontais, temos n(x) = 3-m(1/4 – x). Significado, n(x) é o resultado de m(x) ser esticado verticalmente por um factor de escala de 3 e esticado horizontalmente por um factor de escala de 1/4,

P>Pelos vistos, observemos as traduções feitas em p(x).

q(x) = 3/4 x – 1 – 1

= 3(x/4) – 1 – 1

= p(x/4) – 1

p>> A partir disto, podemos ver que q(x) resulta de p(x) ser esticado horizontalmente por um factor de escala de 1/4 e traduzido por uma unidade para baixo.

Exemplo 8

Quais são as transformações feitas em f(x) para que resultem em g(x) = 2|x/3| – 1? Use o gráfico de f(x) mostrado abaixo para o guiar. Aplique as transformações no gráfico g(x).

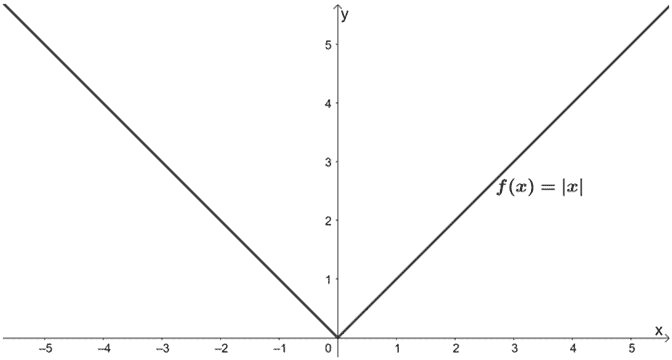
Solução

P>Vamos prosseguir e expressar g(x) em termos de f(x).

p>g(x) = 2 – |1/3 – x| – 1

= 2- f(x/3) – 1

Isto significa que as traduções em f(x) para obter g(x) são:

• Horizontalmente esticadas por um factor de escala de 1/3.
• Estirado verticalmente por um factor de escala de 2,
• Traduzido para baixo por 1 unidade.

Vamos aplicar lentamente estas transformações em f(x), começando por esticar horizontalmente f(x).

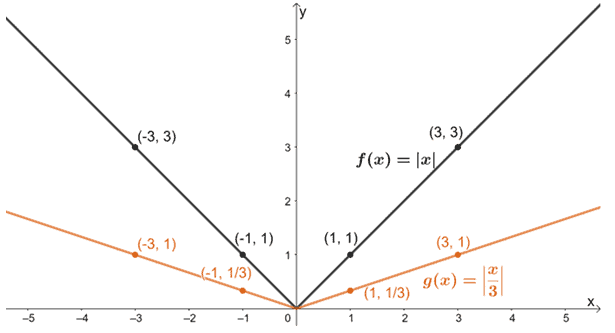
Vamos agora esticar o gráfico resultante verticalmente por um factor de escala de 2.

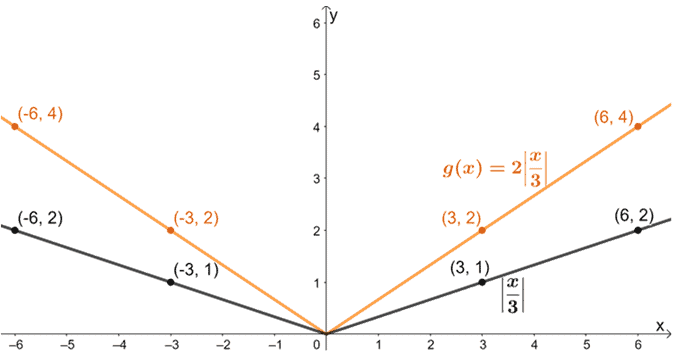
Lastly, vamos traduzir o gráfico uma unidade para baixo.

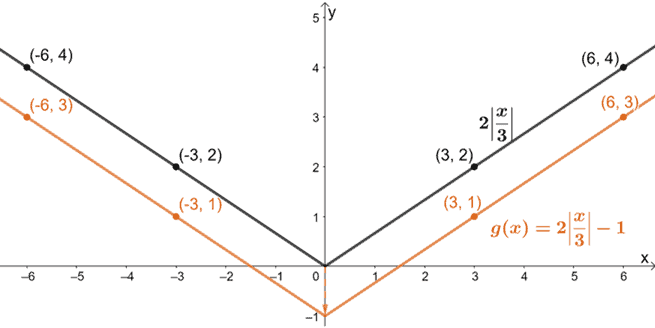
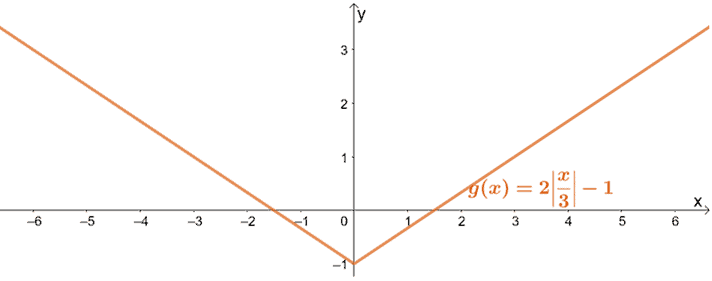
Hence, acabámos de mostrar como g(x) pode ser agarrado usando a função pai de funções de valor absoluto, f(x) = |x|.

Perguntas Práticas

1. A função, g(x), é obtida por estiramento horizontal f(x) = 16×2 por um factor de escala de 2. Qual das seguintes é a expressão correcta para g(x)?

a. g(x) = 32×2

b. g(x) = 16×2

c. g(x) = 8×2

d. g(x) = 2×2

2. Escreva as expressões para g(x) e h(x) em termos de f(x) dadas as seguintes condições:

a. A função g(x) é o resultado de f(x) ser esticado horizontalmente por um factor de 1/4.

b. Quando esticamos horizontalmente g(x) por um factor de escala de 1/3, obtemos h(x).

3. A função, f(x), passa através do ponto (10, 8). Se f(x) é horizontalmente esticado por um factor de escala de 5, qual seria a nova coordenada x do ponto?

4. A tabela de valores para f(x) é mostrada abaixo. Se g(x) é o resultado de f(x) ser esticado horizontalmente por um factor de escala de 3, construa a sua tabela de valores e mantenha os valores da corrente de saída.

x	-9	-6	-3	0	3	6	9
f(x)	-17	-11	-5	1	7	13	19

5. Observar as funções mostradas abaixo. Qual é a relação entre f(x) e g(x)?

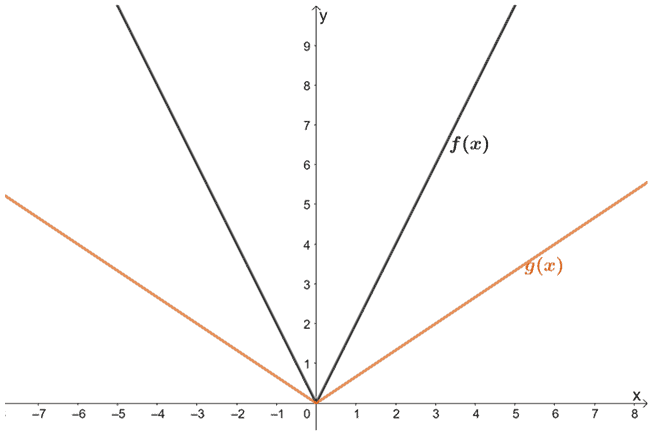
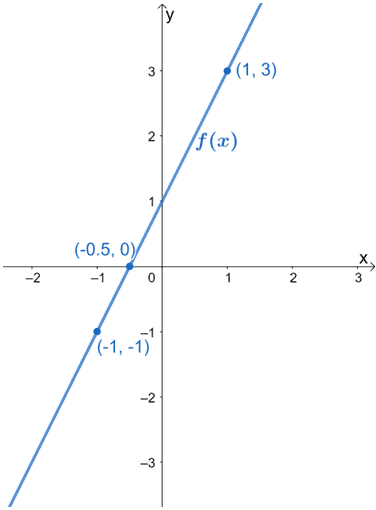
6. A imagem abaixo mostra o gráfico de f(x). Gráfico h(x) utilizando o facto de ser o resultado de f(x) ser esticado horizontalmente por um factor de 1/3. Certifique-se de incluir os novos pontos críticos para g(x).

7. Descreva as transformações feitas nas seguintes funções mostradas abaixo.

a. f(x) = x2 → g(x) = x2/16

b. m(x) = √x → n(x) = √(x/5) + 3

c. p(x) = 2x + 1→ q(x) = 2x/3 + 2

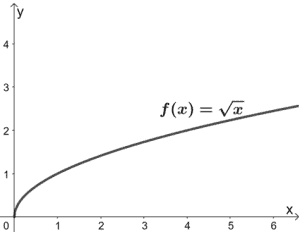
8. Quais são as transformações feitas em f(x) para que resultem em g(x) = 3√(x/2)? Utilize o gráfico de f(x) mostrado abaixo para o guiar. Aplique as transformações no gráfico g(x).

Imagens/desenhos matemáticos são criados com GeoGebra.