Inversão de Matriz: Encontrar o Inverso de uma Matriz

p>Voltar ao Índice de Lições | Fazer as Lições por Ordem | Página Amigável para Impressão

Inversão de Matriz:
Encontrar o Inverso de uma Matriz (página 1 de 2)

Para matrizes, não existe divisão. Pode-se adicionar, subtrair, e multiplicar matrizes, mas não se pode dividi-las. Existe, no entanto, um conceito relacionado, que se chama “inversão”. Primeiro vou discutir porque é que a inversão é útil, e depois vou mostrar-lhe como fazê-lo.

P>Pense em quando aprendeu pela primeira vez como resolver equações lineares. Se lhe fosse dado algo como “3x = 6”, resolveria dividindo ambos os lados por 3. Uma vez que multiplicar por1/3 é o mesmo que dividir por 3, também poderia multiplicar ambos os lados por 1/3 para obter a mesma resposta: x = 2. Se precisasse de resolver algo como “(3/2)x = 6”, ainda poderia dividir ambos os lados por 3/2, mas provavelmente era mais fácil multiplicar ambos os lados por 2/3. A fracção recíproca 2/3 é o inverso de 3/2 porque, se multiplicar as duas fracções, obtém-se 1, que é, neste contexto, chamada “a identidade (multiplicativa)”: 1 é chamada a identidade porque multiplicar algo por 1 não altera o seu valor.

Esta terminologia e estes factos são muito importantes para as matrizes. Se lhe for dada uma equação matricial como AX = C, onde lhe é dada A e C e lhe é dito para calcular X, você gostaria de “dividir” a matriz A. Mas não se pode fazer a divisão com matrizes. Por outro lado, e se conseguisse encontrar o inverso de A, algo semelhante a encontrar a fracção recíproca acima? O inverso de A, escrito como “A-1” e pronunciado “A inverso”, permitir-lhe-ia cancelar o A da equação da matriz e depois resolver para X.

p>

AX = C
A-1AX = A-1C
IX = A-1C
X = A-1C

Como é que “A-1AX” no lado esquerdo da equação se transformou em “X”? Pense novamente na natureza dos inversos para números regulares. Se tiver um número (tal como 3/2) e o seu inverso (neste caso, 2/3) e os multiplicar, obtém-se 1. E 1 é a identidade, assim chamada porque 1x = x para qualquer número x. Funciona da mesma forma para as matrizes. Se se multiplicar uma matriz (como A) e o seu inverso (neste caso,
A-1), obtém-se a matriz de identidade I. E o ponto da matriz de identidade é que IX = X para qualquer matriz X (significando “qualquer matriz do tamanho correcto”, claro).

De notar que a ordem na multiplicação acima é importante e não é de modo algum arbitrária. Recordar que, para as matrizes, a multiplicação não é comutativa. Ou seja, AB quase nunca é igual a BA. Portanto, multiplicar a equação matricial “à esquerda” (para obter A-1AX) não é de todo a mesma coisa que multiplicar “à direita” (para obter AXA-1). E não se pode dizer que o produto AXA-1 é igual a A-1AX, porque não se pode mudar a ordem na multiplicação. Em vez disso, é preciso multiplicar A-1 à esquerda, colocando-o ao lado de A na equação matriz original. E como tem de fazer o mesmo a ambos os lados de uma equação quando está a resolver, tem de multiplicar “à esquerda” também no lado direito da equação, resultando em A-1C. Não pode ser casual com a colocação das matrizes; deve ser preciso, correcto, e consistente. Esta é a única forma de cancelar A com sucesso e resolver a equação matricial.

Como viu acima, as matrizes inversas podem ser muito úteis para resolver equações matriciais. Mas, dada uma matriz, como é que se inverte? Como se encontra o inverso? A técnica de inversão de matrizes é um pouco inteligente. Para uma dada matriz A e o seu inverso A-1, sabemos que temos A-1A = I. Vamos utilizar a matriz de identidade I no processo de inversão de uma matriz.

• Encontrar o inverso da matriz seguinte.

P>Primeiro, escrevo as entradas da matriz A, mas escrevo-as numa matriz de dupla largura:

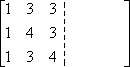
Na outra metade da largura dupla, escrevo a matriz de identidade:

Agora vou fazer operações de linha de matriz para converter o lado esquerdo da dupla largura na identidade. (Como sempre com operações em fila, não há uma forma “certa” de o fazer. O que se segue são apenas os passos que me aconteceram. Os seus cálculos podem facilmente parecer bastante diferentes.)

Agora que o lado esquerdo da dupla largura contém a identidade, o lado direito contém o inverso. Ou seja, a matriz inversa é a seguinte:

Nota que podemos confirmar que esta matriz é o inverso de A, multiplicando as duas matrizes e confirmando que obtemos a identidade: Copyright © Elizabeth Stapel 2003-2011 Todos os direitos reservados

Sejam informados de que, na “vida real”, o inverso raramente é uma matriz preenchida com números inteiros bem arrumados como este. Com alguma sorte, no entanto, especialmente se estiver a fazer inversos à mão, ser-lhe-ão dados números inteiros simpáticos como este para fazer.

Top | 1 | 2 | Voltar ao Índice Seguinte >>