Qual é o maior número?
Números continuam para sempre – mas no caminho para o infinito, há alguns posts bastante remotos.
Para os nossos antepassados, um milhão era tão grande como os números necessários para obter. Não havia necessidade de invocar os milhares de milhões (1.000.000.000) de finanças ou os terabytes (1012) de informática. A tecnologia fez-nos blasé sobre a utilização de números de 9 ou 12 dígitos na conversa. No entanto, há um longo caminho a percorrer antes mesmo de alcançarmos a escala do nosso lugar no universo, quanto mais os números vertiginosamente gigantescos que os matemáticos sonharam.
Números padrão
Past um bilião – a ordem de grandeza da população humana – temos realmente de nos despedir da ideia de ter nomes para os números. (Embora existam até 1063, não são de uso comum). Para a distância a luz viaja num minuto, o número de átomos num grama de carbono, ou a distância entre galáxias, os cientistas usam o formulário padrão para se expressarem. O formulário padrão regista todos os números no formato a × 10n, onde a é um número entre 1 e 10 e n pode ser qualquer número. É o que se usaria para falar sobre o número de átomos de carbono numa amostra de 12g. Que, aliás, é 6,22 × 1023, número de Avogadro, e bastante grande. O universo observável tem cerca de 8,8 × 1023 km de largura, e estima-se que existam 1087 partículas nele. Mas maiores que esses números são, de longe, as construções das mentes matemáticas.
Deixe-me googol it for you
Immortalizado em uso comum pelo gigante da Internet, um googol é o número 10100 – 10, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000. O matemático americano Edward Kasner pediu ao seu sobrinho Milton para lhe dar um nome, e tornou-se um googol. Mas o próximo número realmente grande é o googolplex, que eleva 10 para o poder de um googol. Isto é astronomicamente maior que um googol – é impossível escrever um googolplex em notação padrão mesmo que se escreva um único dígito em cada partícula no universo.
O poder dos poderes
Adicionar um exponencial ao exponente aumenta realmente a taxa de aumento dos números.
3×3×3=27
3(33) = 7,625,597,484,987
Naturalmente, na busca de números maiores, adicionar-se-iam cada vez mais potências à torre. No entanto, isto torna-se rapidamente embaraçoso de anotar, além de resultar em torres que fazem com que o aspecto de Pisa pareça estável. A alteração da notação permite condensar estas torres e exprimir conceitos mais elevados.
Sigam as setas
Desenvolvendo outra forma de denotar poderes:
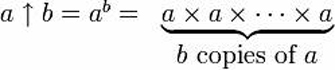
Donald Knuth cunhou um novo operador para exponenciação repetida (“tetração”), para trazer essas torres de poder à terra.
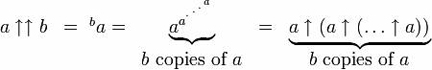
Em uso, a seta dupla tem este aspecto:
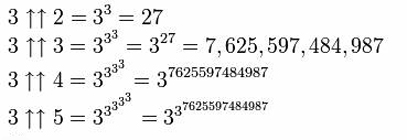
Esta pode ser estendida ainda mais, adicionando uma terceira seta, criando a operação de ‘pentation’ – tetração repetida.
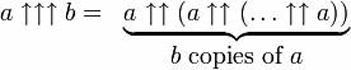
Em palavras, isso envolve a tetração de a ao a (portanto, uma torre de energia de um ‘a’s), e depois a construção de outra torre de ‘a’s tão alta como essa torre de energia, depois utilizando o resultado dessa torre de energia para determinar o número de ‘a’s na torre seguinte -resultando no cálculo das torres de energia b, aumentando em altura de acordo com o resultado da tetração anterior.
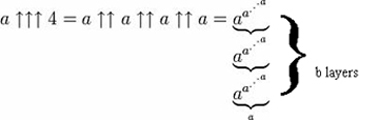
E ainda podem ser adicionadas mais setas, embora pensando nas operações que elas denotam possa exigir mais tempo ao cérebro do que o que está preparado para dedicar à questão. Mas armados com esta notação, podemos agora reconhecer alguns números verdadeiramente grandes.
Chamar Ackermann e Graham
Provas matemáticas deram-nos algumas quantidades massivas. No início do século XX, os matemáticos queriam saber como dizer se uma sequência era calculável – poderia ser definido um processo mecânico para a sua elaboração? Foi proposto que uma sequência fosse calculável se tivesse a propriedade de ser ‘recursiva primitiva’. Wilhelm Ackermann atirou uma chave de porcas em forma de sequência ao cunhar uma sequência que, embora calculável, não era recursiva primitiva. E assim:
Inicie com a operação matemática mais simples possível – adição. Aplicar isto ao primeiro número natural, 1:
1 + 1 = 2
Então avançar para a operação seguinte, multiplicação (adição repetida). Faça isto para o próximo número:
2 × 2 = 4
Nextra multiplicação repetida – exponenciação para si e para mim – com 3 como variável.
33 = 27
Até agora, tão insignificante. Mas acabámos de definir uma função para exponenciação repetida, tetração, e se fizermos isto a 4..
![]()
Parece pequeno, tem 10154 dígitos. E este é apenas o 4º termo na sequência.
Fifth é … uma torre de potência de fives
dígitos altos.
Sixth é . Apenas cinco símbolos denotam um número maior do que há lugar no universo, mesmo que se escreva cada dígito numa fonte de 1nm de largura. E a sequência continua.
A mesma notação de seta para cima foi utilizada por Ronald Graham para limitar algumas propriedades de um hipercubo (um cubo em 4 dimensões espaciais), embora ‘o número de Graham’ seja agora mais conhecido simplesmente por ser colossal.
O número de Graham é definido desta forma:

O número de setas em cada camada é dado pelo resultado da avaliação das setas na camada abaixo, até que após 64 camadas, o número final seja alcançado. Para ter uma ideia do tamanho disto, podemos olhar apenas para a primeira camada:

onde o número de três na expressão da direita é
![]()
Agora cada tetração () operação reduz-se a uma “torre” de exponenciações (
) de acordo com a definição
![]()
onde existem X três.
Thus,
![]()
onde o número de três é , torna-se, apenas em termos de repetidas “torres de exponenciação”, e onde o número de três em cada torre, começando pela torre mais à esquerda, é especificado pelo valor da torre seguinte à direita.
Isto é, tecnicamente falando, um lote de três. Mas não relaxe ainda, pois o número de Graham, embora sendo o maior número que os matemáticos ainda precisaram de escrever explicitamente, é anão por alguns produtos da teoria da computação. Não temos espaço para entrar neles aqui, mas veja ‘Quem pode escrever o número maior?’ de Scott Aaronson se o número de Graham’s simplesmente não foi suficiente para si. Também entra em mais detalhes sobre a história dos grandes números e as suas explicações.
Big, Bigger, Biggest
O mundo dos números é, como seria de esperar, infinito. A natureza é bastante grande, mas os números que ela exige que utilizemos são muito menores do que aqueles que os matemáticos humanos sonharam. Nesse sentido, a mente humana é maior do que o universo.