Selecção do melhor algoritmo de Aprendizagem Máquina para o seu problema de regressão

comecei recentemente um livro…boletim informativo educacional focalizado. Book Dives é um boletim informativo quinzenal onde para cada novo número mergulhamos num livro de não-ficção. Aprenderá sobre as principais lições do livro e como aplicá-las na vida real. Pode subscrevê-lo aqui.

Ao abordar qualquer tipo de problema de Aprendizagem Mecânica (ML), há muitos algoritmos diferentes à escolha. Na aprendizagem de máquinas, há algo chamado teorema “Sem Almoço Livre” que basicamente declara que nenhum algoritmo ML é melhor para todos os problemas. O desempenho dos diferentes algoritmos ML depende fortemente do tamanho e da estrutura dos seus dados. Assim, a escolha correcta do algoritmo permanece frequentemente pouco clara, a menos que testemos os nossos algoritmos directamente através de tentativas e erros antigos.

Mas, existem alguns prós e contras a cada algoritmo ML que podemos usar como orientação. Embora um algoritmo nem sempre seja melhor que outro, existem algumas propriedades de cada algoritmo que podemos usar como guia na selecção rápida do correcto e na afinação de hiperparâmetros. Vamos dar uma vista de olhos a alguns algoritmos ML proeminentes para problemas de regressão e definir orientações para quando usá-los com base nos seus pontos fortes e fracos. Este post deverá então servir como uma grande ajuda na selecção do melhor algoritmo ML para o seu problema de regressão!

p>Apenas antes de entrarmos, consulte o Boletim Inteligente de IA para ler o mais recente e melhor sobre IA, Aprendizagem de Máquina, e Ciência de Dados!

Regressão Linear e Polinomial

div>

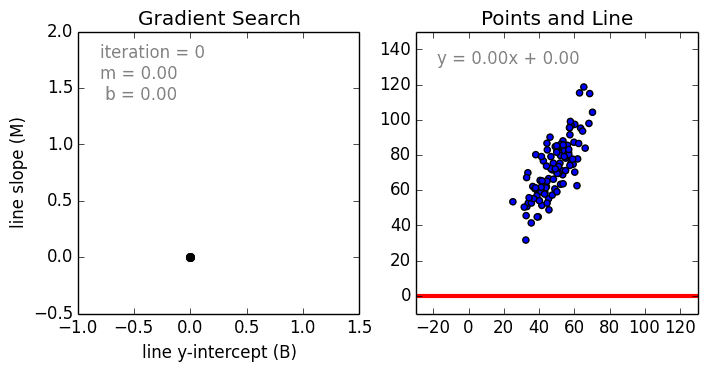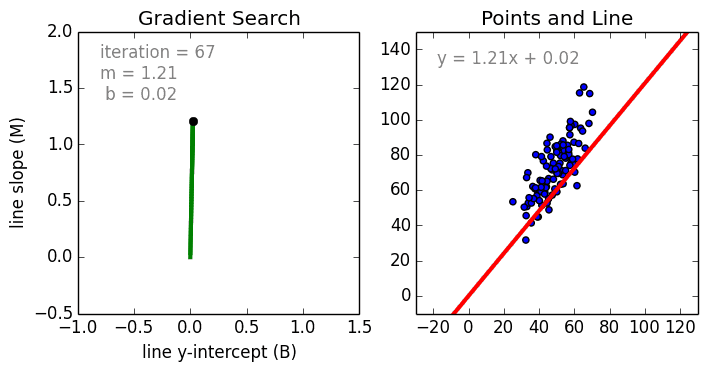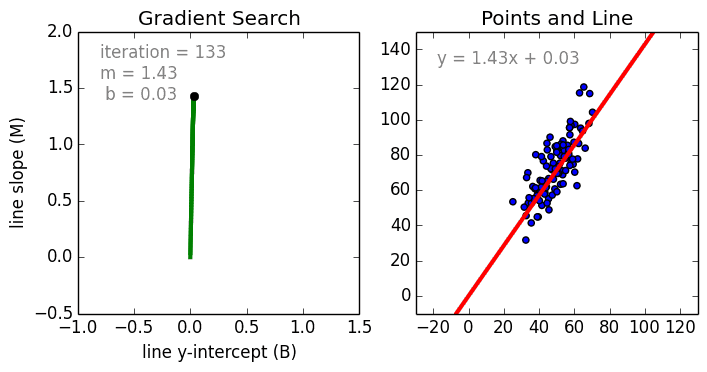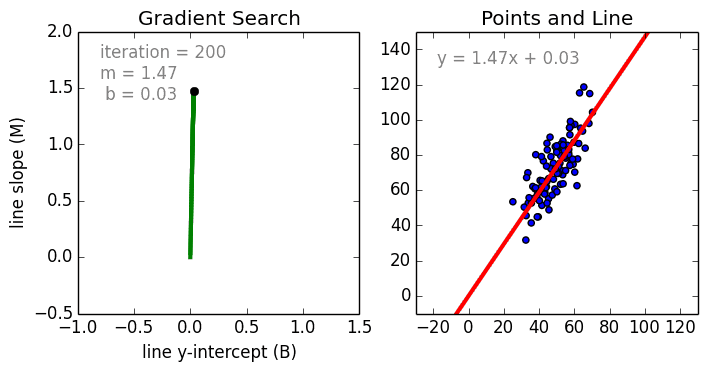
Bomeçando com o caso simples, A Regressão Linear Variável Única é uma técnica utilizada para modelar a relação entre uma variável independente de entrada única (variável de característica) e uma variável dependente de saída utilizando um modelo linear i.e uma linha. O caso mais geral é a Regressão Linear de Múltiplas Variáveis onde é criado um modelo para a relação entre múltiplas variáveis independentes de entrada (variáveis de característica) e uma variável dependente de saída. O modelo permanece linear na medida em que a saída é uma combinação linear das variáveis de entrada.

Há um terceiro caso mais geral chamado Regressão Polinomial onde o modelo se torna agora uma combinação não linear das variáveis de característica, ou seja, pode haver variáveis exponenciais, seno e cosseno, etc. No entanto, isto requer o conhecimento de como os dados se relacionam com o resultado. Os modelos de regressão podem ser treinados usando a Descendência Gradiente Estocástica (SGD).

Pros:

• Fast para modelar e é particularmente útil quando a relação a ser modelada não é extremamente complexa e se não se tiver muitos dados.
• Regressão linear é simples de compreender, o que pode ser muito valioso para decisões empresariais.

Cons:

• Para dados não lineares, a regressão polinomial pode ser bastante desafiante de desenhar, uma vez que é preciso ter alguma informação sobre a estrutura dos dados e a relação entre as variáveis de característica.
• Como resultado do acima exposto, estes modelos não são tão bons como outros quando se trata de dados altamente complexos.

Neural Networks

p>A Neural Network consiste num grupo de nós interligados chamados neurónios. As variáveis de característica de entrada dos dados são transmitidas a estes neurónios como uma combinação linear multi-variável, onde os valores multiplicados por cada variável de característica são conhecidos como pesos. Uma não linearidade é então aplicada a esta combinação linear que dá à rede neural a capacidade de modelar relações complexas não lineares. Uma rede neural pode ter múltiplas camadas onde a saída de uma camada é passada para a seguinte da mesma forma. Na saída, geralmente não é aplicada qualquer não-linearidade. As redes neurais são treinadas utilizando a Descendência Gradiente Estocástica (SGD) e o algoritmo de retropropagação (ambos apresentados no GIF acima).

p>Pros:

• As redes neurais podem ter muitas camadas (e portanto parâmetros) com não-linearidades, são muito eficazes na modelação de relações não-lineares altamente complexas.
• Não temos geralmente de nos preocupar com a estrutura dos dados nas redes neurais são muito flexíveis na aprendizagem de quase todos os tipos de relações variáveis de características.
• A investigação tem mostrado consistentemente que simplesmente dar à rede mais dados de formação, quer sejam totalmente novos ou de aumentar o conjunto de dados original, beneficia o desempenho da rede.

Cons:

• Devido à complexidade destes modelos, não são fáceis de interpretar e compreender.
• Podem ser bastante desafiantes e computacionalmente intensivos para treinar, exigindo uma afinação hiper-paramétrica cuidadosa e a definição do horário da taxa de aprendizagem.
• Requerem muitos dados para atingir um elevado desempenho e são geralmente superados por outros algoritmos ML em casos de “pequenos dados”.

Árvores de Regressão e Florestas Aleatórias

div>

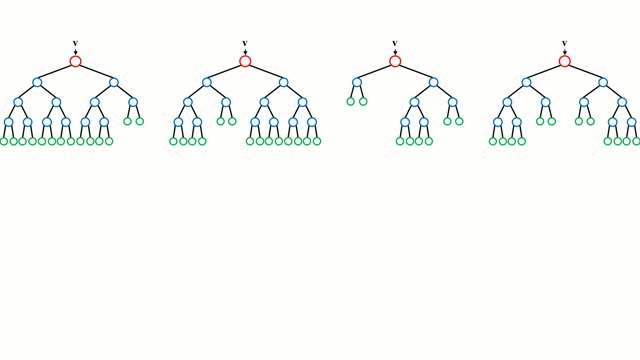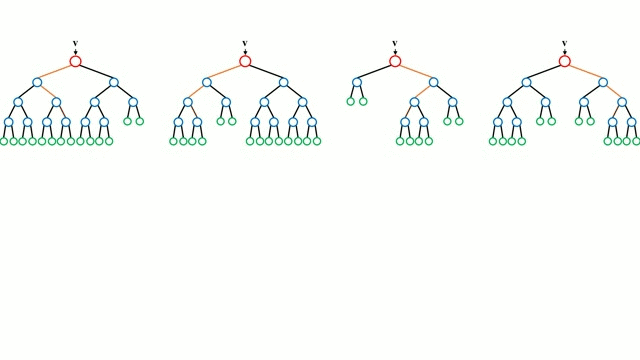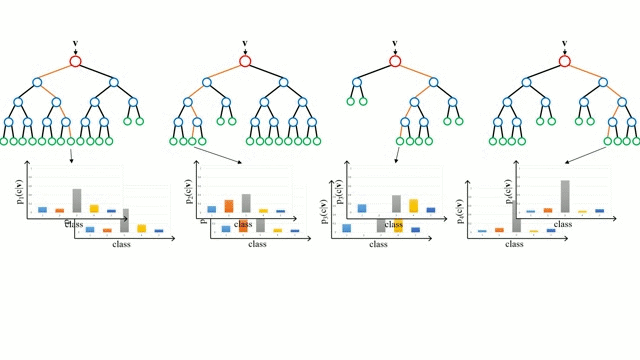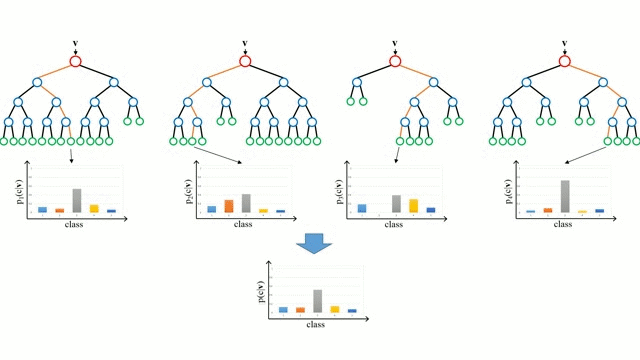
Bem início com a caixa base, uma Árvore de Decisão é um modelo intuitivo onde por um percorre os ramos da árvore e selecciona o ramo seguinte para descer com base numa decisão num nó. A indução em árvore é a tarefa de tomar um conjunto de instâncias de formação como input, decidindo quais os atributos melhores para dividir, dividindo o conjunto de dados, e recurrindo nos conjuntos de dados resultantes da divisão até que todas as instâncias de formação sejam categorizadas. Durante a construção da árvore, o objectivo é dividir nos atributos que criam os nós de criança mais puros possíveis, o que manteria ao mínimo o número de partições que teriam de ser feitas para classificar todas as instâncias no nosso conjunto de dados. A pureza é medida pelo conceito de ganho de informação, que se relaciona com o quanto seria necessário saber sobre uma instância anteriormente não vista para que esta fosse devidamente classificada. Na prática, isto é medido comparando a entropia, ou a quantidade de informação necessária para classificar uma única instância de uma partição do conjunto de dados actual, com a quantidade de informação para classificar uma única instância se a partição do conjunto de dados actual fosse mais particionada num dado atributo.

As Florestas Aleatórias são simplesmente um conjunto de árvores de decisão. O vector de entrada é executado através de múltiplas árvores de decisão. Para a regressão, o valor de saída de todas as árvores é a média; para a classificação é utilizado um esquema de votação para determinar a classe final.

Pros:

• Great at learning complex, highly non-linear relationships. Normalmente podem atingir um desempenho bastante elevado, melhor do que a regressão polinomial e muitas vezes ao nível das redes neurais.
• Muito fácil de interpretar e compreender. Embora o modelo final treinado possa aprender relações complexas, os limites de decisão que são construídos durante o treino são fáceis e práticos de compreender.

Cons:

• Por causa da natureza das árvores de decisão de treino, elas podem ser propensas a grandes sobreajustamentos. Um modelo completo de árvore de decisão pode ser excessivamente complexo e conter estrutura desnecessária. Embora isto possa por vezes ser aliviado utilizando a poda adequada de árvores e conjuntos florestais aleatórios maiores.
• Utilizar conjuntos florestais aleatórios maiores para alcançar um desempenho superior tem os inconvenientes de ser mais lento e requerer mais memória.

Conclusão

Boom! Eis os seus prós e contras! No próximo post vamos ver os prós e os contras de diferentes modelos de classificação. Espero que tenham gostado deste post e que tenham aprendido algo novo e útil. Se gostou, sinta-se à vontade para lhe dar algumas palmas.