Was ist die größte Zahl?

Zahlen gehen unendlich weiter – aber auf dem Weg ins Unendliche gibt es einige ziemlich weit entfernte Wegpunkte.

Für unsere Vorfahren war eine Million so groß, wie Zahlen nur sein konnten. Es war nicht nötig, sich auf die Milliarden (1.000.000.000) der Finanzwelt oder die Terabytes (1012) der Computertechnik zu berufen. Die Technologie hat uns dazu gebracht, dass wir uns nicht mehr über 9- oder 12-stellige Zahlen unterhalten. Es ist jedoch noch ein weiter Weg, bis wir die Größenordnung unseres Platzes im Universum erreicht haben, ganz zu schweigen von den schwindelerregend gigantischen Zahlen, die sich die Mathematiker ausgedacht haben.

Standardzahlen

Nach einer Milliarde – der Größenordnung der menschlichen Bevölkerung – müssen wir uns eigentlich von der Idee verabschieden, Namen für Zahlen zu haben. (Bis 1063 gibt es sie zwar, aber sie sind nicht gebräuchlich). Für die Entfernung, die Licht in einer Minute zurücklegt, die Anzahl der Atome in einem Gramm Kohlenstoff oder die Entfernung zwischen Galaxien verwenden Wissenschaftler die Standardform, um sich auszudrücken. Die Standardform zeichnet alle Zahlen im Format a × 10n auf, wobei a eine Zahl zwischen 1 und 10 ist und n eine beliebige Zahl sein kann. Es ist das, was Sie verwenden würden, um über die Anzahl der Kohlenstoffatome in einer 12g Probe zu sprechen. Diese ist übrigens 6,22 × 1023, die Avogadrosche Zahl, und damit ziemlich groß. Das beobachtbare Universum ist etwa 8,8 × 1023 km groß, und es gibt schätzungsweise 1087 Teilchen darin. Aber weitaus größer als diese Zahlen sind die Konstrukte der mathematischen Köpfe.

Lassen Sie es mich für Sie googeln

Im allgemeinen Sprachgebrauch durch den Internet-Giganten verewigt, ist ein Googol die Zahl 10100 – 10, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000. Der amerikanische Mathematiker Edward Kasner bat seinen Neffen Milton, sie zu benennen, und es wurde ein Googol. Aber die nächste wirklich große Zahl ist das Googolplex, das 10 hoch ein Googol erhöht. Das ist astronomisch größer als ein Googol – es ist unmöglich, ein Googolplex in Standardnotation aufzuschreiben, selbst wenn man jedes Teilchen im Universum mit einer einzelnen Ziffer versehen würde.

Die Potenz der Potenzen

Das Hinzufügen eines Exponentials zum Exponenten erhöht die Rate der Vergrößerung von Zahlen wirklich.

3×3×3=27

3(33) = 7.625.597.484.987

Natürlich würde man auf der Suche nach größeren Zahlen immer mehr Potenzen anhängen. Das wird aber schnell umständlich zu notieren und führt zu Türmen, die die von Pisa stabil aussehen lassen. Eine veränderte Notation ermöglicht es, diese Türme zu verdichten und höhere Konzepte auszudrücken.

Folgt den Pfeilen

Eine andere Art, Potenzen zu bezeichnen:

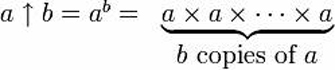
Donald Knuth prägte einen neuen Operator für die wiederholte Potenzierung („Tetration“), um diese Potenztürme auf die Erde zu bringen.

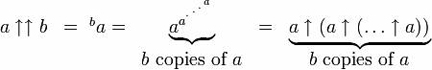
Im Gebrauch sieht der Doppelpfeil so aus:

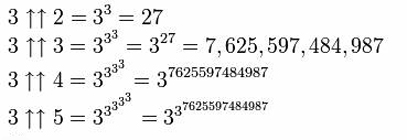
Dies kann noch erweitert werden, indem ein dritter Pfeil hinzugefügt wird, wodurch die Operation der „Pentation“ – der wiederholten Tetration – entsteht.

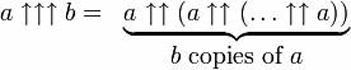
In Worten bedeutet das, dass man a zum a tetriert (also einen Powerturm aus a’s), dann einen weiteren Turm aus a’s baut, der genauso hoch ist wie dieser Powerturm, dann wird das Ergebnis dieses Powerturms verwendet, um die Anzahl der ‚a’s im nächsten Turm zu bestimmen – mit dem Ergebnis, dass b Powertürme berechnet werden, die entsprechend dem Ergebnis der vorherigen Tetration in der Höhe zunehmen.

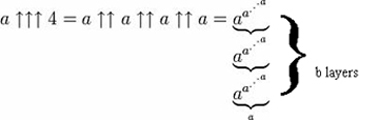
Und es können noch weitere Pfeile hinzugefügt werden, obwohl das Nachdenken über die Operationen, die sie bezeichnen, mehr Gehirnzeit erfordern könnte, als Sie bereit sind, dem Thema zu widmen. Aber mit dieser Notation bewaffnet, können wir nun einige wirklich große Zahlen anerkennen.

Aufruf von Ackermann und Graham

Mathematische Beweise haben uns einige gewaltige Mengen gegeben. Zu Beginn des 20. Jahrhunderts wollten Mathematiker wissen, wie man feststellen kann, ob eine Folge berechenbar ist – könnte man einen mechanischen Prozess definieren, um sie zu berechnen? Es wurde vorgeschlagen, dass eine Folge berechenbar ist, wenn sie die Eigenschaft hat, „primitiv rekursiv“ zu sein. Wilhelm Ackermann hat dem Ganzen einen Strich durch die Rechnung gemacht, indem er eine Sequenz prägte, die zwar berechenbar, aber nicht primitiv rekursiv war. Und die geht so:

Starten Sie mit der einfachsten mathematischen Operation, die möglich ist – der Addition. Wenden Sie diese auf die erste natürliche Zahl an, 1:

1 + 1 = 2

Gehen Sie dann zur nächsten Operation über, der Multiplikation (wiederholte Addition). Machen Sie dies mit der nächsten Zahl:

2 × 2 = 4

Als Nächstes kommt die wiederholte Multiplikation – für Sie und mich die Potenzierung – mit 3 als Variable.

33 = 27

So weit, so mickrig. Aber wir haben gerade eine Funktion zur wiederholten Potenzierung definiert, die Tetration, und wenn wir das mit 4 machen..

Sieht klein aus, hat 10154 Stellen. Und das ist nur der 4. Term in der Folge.

Der fünfte ist … ein Powerturm aus fünf Ziffern hoch.

Sechstel ist . Nur fünf Symbole bezeichnen eine Zahl, die größer ist, als im Universum Platz hat, selbst wenn man jede Ziffer in einer 1nm breiten Schrift schreiben würde. Und die Reihe geht weiter.

Die gleiche Pfeil-nach-oben-Notation wurde von Ronald Graham verwendet, um einige Eigenschaften eines Hyperwürfels (ein Würfel in 4 Raumdimensionen) einzuschränken, obwohl die „Grahamsche Zahl“ heute besser bekannt ist, weil sie einfach kollossal ist.

Die Grahamsche Zahl ist wie folgt definiert:

Die Anzahl der Pfeile in jeder Schicht ergibt sich aus dem Ergebnis der Auswertung der Pfeile in der darunter liegenden Schicht, bis nach 64 Schichten die endgültige Anzahl erreicht ist. Um Ihnen eine Vorstellung von der Größe zu geben, können wir uns die erste Ebene allein ansehen:

wobei die Anzahl der Dreier im Ausdruck rechts ist

Jetzt reduziert sich jede Tetration () Operation auf einen „Turm“ von Potenzierungen () gemäß der Definition

wo es X Dreier gibt.

So wird,

wo die Anzahl der Dreier ist,, ausschließlich in Form von wiederholten „Potenzierungstürmen“, wobei die Anzahl der Dreier in jedem Turm, beginnend mit dem ganz linken Turm, durch den Wert des nächsten Turms rechts daneben bestimmt wird.

Das ist, technisch gesehen, eine Menge von Dreien. Entspannen Sie sich aber noch nicht, denn die Grahamsche Zahl ist zwar die größte Zahl, die Mathematiker bisher explizit aufschreiben mussten, wird aber von einigen Produkten der Rechentheorie in den Schatten gestellt. Wir haben hier nicht genug Platz, um auf sie einzugehen, aber schauen Sie sich „Who can write down the bigger number?“ von Scott Aaronson an, wenn Ihnen Grahams Zahl noch nicht genug war. Es geht auch mehr ins Detail über die Geschichte der großen Zahlen und ihre Erklärungen.

Groß, größer, am größten

Die Welt der Zahlen ist, wie Sie vielleicht erwarten, unendlich. Die Natur ist ziemlich groß, aber die Zahlen, die sie von uns verlangt, sind viel kleiner als die, die sich die menschlichen Mathematiker ausgedacht haben. In diesem Sinne ist der menschliche Geist größer als das Universum.