Zeitmaße: Biennium, Lustrum, Dekade, Jahrhundert, Millennium
In diesem Beitrag schauen wir uns Zeitmaße an, die sich auf Mengen von Jahren beziehen: Biennium, Lustrum, Dekade, Jahrhundert, Millenium
Wenn Sie sich frühere Beiträge über Zeiteinheiten ansehen möchten, können Sie das hier tun:
- Lernen Sie, wie man Zeit misst und welche Einheiten damit verbunden sind
- Zeit: Grundlegende Konzepte zum Erlernen der Zeitmessung
- Zeitmessungsprobleme: einfache und komplexe Formen
Bevor Sie weiterlesen, müssen Sie vor allem Folgendes verstehen:

Wir werden diese Konzepte anhand einiger Probleme üben, die Sie während Ihrer täglichen Smartick-Sitzungen finden können. Fangen wir an!
Problem 1
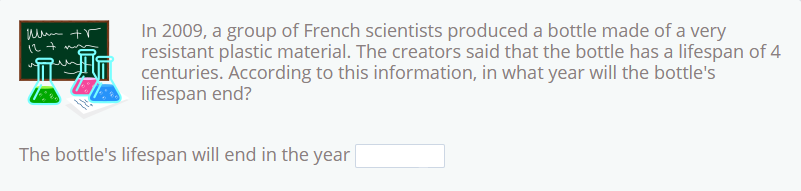
Um dieses Problem zu lösen, müssen wir uns merken, dass ein Jahrhundert 100 Jahre sind, also sind 4 Jahrhunderte 4×100=400 Jahre.
Da wir das wissen, müssen wir diese 400 Jahre einfach zu dem Jahr addieren, in dem die Flasche hergestellt wurde, 2009.
Daher 2009 + 400 = 2409
Antwort: Die Lebensdauer der Flasche endet im Jahr 2409
Problem 2
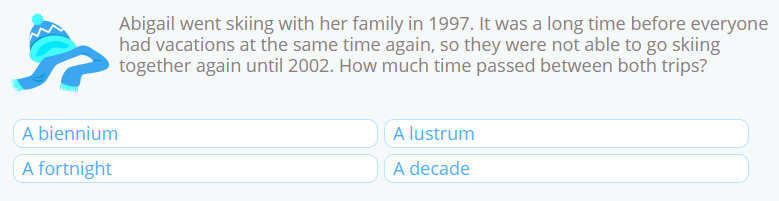
Um dieses Problem zu lösen, müssen wir die Daten subtrahieren.
2002 – 1997 = 5
Die Zeiteinheit, die 5 Jahren entspricht, ist ein Lustrum.
Antwort: Zwischen beiden Reisen verging ein Lustrum
Problem 3

Um dieses Problem zu lösen, müssen wir zunächst die Anzahl der Jahre berechnen, die zwischen 3655 v. Chr. und 2010 vergehen.
Um das zu tun, addieren wir 3655 und 2010. 3655 + 2010 = 5665
Nun müssen wir diese Zeitspanne in kleinere Einheiten aufteilen.
5000 Jahre sind 5 Jahrtausende
600 Jahre sind 6 Jahrhunderte
60 Jahre sind 6 Jahrzehnte
5 Jahre sind ein Lustrum
Daher sind 5 Jahrtausende + 6 Jahrhunderte + 6 Jahrzehnte + ein Lustrum
Antwort: Es sind 5 Jahrtausende, 6 Jahrhunderte, 6 Jahrzehnte und ein Lustrum vergangen
Problem 4

Um dieses Problem zu lösen, müssen wir zunächst berücksichtigen, dass der Felsen jetzt 1/4 seiner ursprünglichen Größe hat, also 3/4 seiner Größe verloren hat.
Wenn für jedes Viertel 13 Lustra vergehen, müssen wir diese Menge mit 3 multiplizieren. 3 x 13 = 39 Lustra
Nun müssen wir nur noch die 39 Lustra mit den 5 Jahren multiplizieren, die jedes Lustrum enthält:
39 x 5 = 195
Antwort: Es wurde 195 Jahre der Erosion ausgesetzt
Ich hoffe, diese Übungen haben Ihnen geholfen, größere Zeiteinheiten zu verstehen. Denken Sie daran, wenn Sie mehr von diesen Problemen üben wollen, melden Sie sich bei Smartick an und machen Sie jeden Tag eine Sitzung.
Lernen Sie mehr:
- Lernen Sie, wie man ein Zeit-Wortproblem löst
- Wie man Probleme der Massenumrechnung löst
- Zeitmessungsprobleme: Einfache und komplexe Formen
- Wie man ein Subtraktionsproblem mit Umgruppieren löst
- Subtraktion mit Anleihen: Eine Erklärung von zwei verschiedenen Algorithmen



- Autor
- Aktuelle Beiträge
Ein multidisziplinäres und multikulturelles Team, das sich aus Mathematikern, Lehrern, Professoren und anderen Bildungsexperten zusammensetzt!
Sie streben danach, die bestmöglichen mathematischen Inhalte zu erstellen.
- Konsekutive Innenwinkel: Was sie sind und wie man sie findet mit Beispielen – 11.03.2021
- Beispiele für Wortprobleme der zweiten Klasse mit Lösungen – 04.02.2021
- Was ist ein stumpfer Winkel? – 15.01.2021