Applications of Algebra

Related Topics:
More Lessons for GRE Math, Math Worksheets
Diese Lektion ist Teil einer Reihe von Lektionen für den Quantitative Reasoning Section of the GRE revised General Test. In dieser Lektion werden wir lernen:

• Anwendungen der Algebra
• Übersetzen von Wörtern in Algebra
• Beispiele für die Verwendung von Algebra zum Lösen von Wortproblemen
  • Durchschnittswert-Wortprobleme
  • Mischungswortprobleme
  • Entfernung, Rate, Time Word Problems
  • Work Word Problems
  • Word Problems that involve Simultaneous Equations
  • Word Problems that involve Inequalities

Anwendungen der Algebra
Das Übersetzen von verbalen Beschreibungen in algebraische Ausdrücke ist ein wesentlicher erster Schritt beim Lösen von Wortproblemen.
Ein paar Beispiele sind unten angegeben.
– Wenn das Quadrat der Zahl x mit 4 multipliziert wird und dann 15 zu diesem Produkt addiert wird, kann das Ergebnis durch 4×2 + 15 dargestellt werden
– Wenn Peters derzeitiges Gehalt s um 15 Prozent erhöht wird, dann ist sein neues Gehalt 1,15s.
– Wenn y Liter Orangensaft auf 5 Personen verteilt werden sollen, so dass eine bestimmte Person 1 Liter bekommt und der Rest des Saftes gleichmäßig auf die restlichen 4 Personen aufgeteilt wird, dann bekommt jede dieser 4 Personen (y – 1) ÷ 4
Dieses Video zeigt, wie man Wörter und Ausdrücke in algebraische Ausdrücke mit Variablen übersetzt.

• Zeigen Sie Schritt-für-Schritt-Lösungen

Beispiele für die Verwendung algebraischer Techniken zum Lösen von Wortproblemen
Wir werden nun einige Beispiele für die Verwendung algebraischer Techniken zum Lösen von Wortproblemen zeigen. Weitere Beispiele für algebraische Wortprobleme finden Sie hier. Durchschnittliche Wortprobleme

Nachfolgend finden Sie Beispiele für Wortprobleme, bei denen es um den Durchschnitt oder das arithmetische Mittel geht.

Beispiel 1:

Ellen hat in 3 Prüfungen die folgenden Punkte erhalten: 82, 74 und 90. Welche Punktzahl muss
Ellen bei der nächsten Prüfung erreichen, damit der Durchschnitt (arithmetisches Mittel) der 4 Prüfungen 85 beträgt?
Lassen Sie x für die Punktzahl in Ellens nächster Prüfung stehen.
Der Durchschnitt der 4 Prüfungen ist

Lösen wir für x, erhalten wir

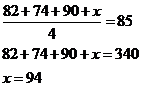
Daher muss Ellen in der nächsten Prüfung eine Punktzahl von 94 erreichen.

Beispiel 2:

In ihren ersten vier Spielen kegelte Jennifer 101, 112, 126, 108. Was ist die Mindestpunktzahl, die sie in ihrem fünften Spiel kegeln muss, um einen Durchschnitt von mindestens 110 zu erreichen?

• Schrittweise Lösungen anzeigen

Wortprobleme mit Gemischen

Im Folgenden finden Sie einige Beispiele für Wortprobleme, die Gemische und Konzentrationen von Gemischen betreffen.

Beispiel 1:
Eine Mischung aus 12 Unzen Essig und Öl ergibt 40 Prozent Essig, wobei alle
Messungen nach Gewicht erfolgen. Wie viele Unzen Öl müssen zu der Mischung hinzugefügt werden, um eine neue Mischung zu erhalten, die nur noch 25 Prozent Essig enthält?
Lassen Sie x für die Anzahl der Unzen Öl stehen, die hinzugefügt werden müssen. Dann ist die Gesamtzahl der Unzen der neuen Mischung 12 + x, und die Gesamtzahl der Unzen Essig in der neuen Mischung ist (0,40)(12). Da die neue Mischung 25 Prozent Essig sein muss, erhalten wir

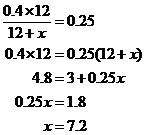
7,2 Unzen Öl müssen hinzugefügt werden, um eine neue Mischung zu erzeugen, die 25 Prozent Essig ist.

Beispiel 2:

Eine Lösung enthält 15 % Salzsäure. Wie viel Wasser muss zu 50 ml dieser Lösung hinzugefügt werden, um sie auf eine 2%ige Lösung zu verdünnen?

• Schrittweise Lösungen anzeigen

Distance, Rate, Time Word Problems

Im Folgenden finden Sie einige Beispiele für Distance, Rate, Time Word Problems.

Beispiel 1:

In einem Fahrwettbewerb fuhren Jeff und Dennis die gleiche Strecke mit einer Durchschnittsgeschwindigkeit von 51
Meilen pro Stunde bzw. 54 Meilen pro Stunde. Wenn Jeff 40 Minuten brauchte, um die Strecke zu fahren, wie lange brauchte dann Dennis?
Lassen Sie x die Zeit in Minuten sein, die Dennis für die Strecke benötigt hat. Die Entfernung d in Meilen ist gleich dem Produkt aus der Geschwindigkeit r in Meilen pro Stunde und der Zeit t in Stunden, d.h. d = rt
Da die Geschwindigkeiten in Meilen pro Stunde angegeben sind, müssen die Zeiten in Stunden ausgedrückt werden, z.B. entsprechen 40 Minuten der einer Stunde.
Mit der Formel, d = rt, erhalten wir folgende Tabelle.

	Entfernung	Rate	Zeit
Jeff	51 ×
Dennis	54 ×

Da die Abstände gleich sind,

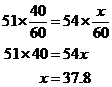
Es dauerte ca. 37.8 Minuten, um die Strecke zu fahren.

Eine Einführung in das Lösen von Wortaufgaben zur gleichförmigen Bewegung (Rate-Zeit-Distanz) mit der Formel Rate x Zeit = Distanz, oder rt=d.
Beispiel:
Zwei Radfahrer starten an der gleichen Ecke und fahren in entgegengesetzte Richtungen. Ein Radfahrer fährt doppelt so schnell wie der andere. In 3 Stunden sind sie 81 km voneinander entfernt. Finden Sie die Geschwindigkeit jedes Radfahrers. Antwort: 9 mph und 18 mph.

• Schrittweise Lösungen anzeigen

Wortproblem mit der Formel für gleichförmige Bewegung rt=d
Beispiel:
Ein Jogger begann mit einer Durchschnittsgeschwindigkeit von 6 mph zu laufen. Eine halbe Stunde später begann ein anderer Läufer nach ihm zu laufen, und zwar von der gleichen Stelle aus mit einer Durchschnittsgeschwindigkeit von 7 mph. Wie lange wird es dauern, bis der Läufer den Jogger eingeholt hat? Antwort: 3 Stunden: 3 Stunden.

• Schrittweise Lösungen anzeigen

Wortproblem unter Verwendung der Formel für gleichförmige Bewegung rt=d
Beispiel:
Eine 555 Meilen lange, 5-stündige Fahrt auf der Autobahn wurde mit zwei Geschwindigkeiten gefahren. Die Durchschnittsgeschwindigkeit des Autos betrug auf dem ersten Teil der Fahrt 105 mph und auf dem zweiten Teil 115 mph. Wie lange ist das Auto bei jeder Geschwindigkeit gefahren? Antwort: 105 mph für 2 Stunden und 115 mph für 3 Stunden.

• Zeigen Sie Schritt-für-Schritt-Lösungen an

Wortproblem unter Verwendung der Formel für gleichförmige Bewegung rt=d
Beispiel:
Andy und Beth befinden sich an gegenüberliegenden Enden einer 18 Meilen langen Landstraße und wollen zur gleichen Zeit losfahren, um sich zu treffen. Andy läuft 7 mph, während Beth 5 mph läuft. Wie lange nach dem Start werden sie sich treffen? Antwort: 1,5 Stunden.

• Schrittweise Lösungen anzeigen

Beispiel:
Ein Auto und ein Bus fahren um 14 Uhr von der gleichen Stelle in die gleiche Richtung los. Die Durchschnittsgeschwindigkeit des Autos ist doppelt so hoch wie die Durchschnittsgeschwindigkeit des Busses. Nach 2 Stunden ist das Auto 68 Meilen vor dem Bus. Ermitteln Sie die Geschwindigkeit des Busses und des Autos. Antwort: Busgeschwindigkeit: 34 mph; Autogeschwindigkeit: 68 mph.

• Schrittweise Lösungen anzeigen

Beispiel:
Ein Pilot flog von einer Stadt zu einer anderen Stadt mit einer Durchschnittsgeschwindigkeit von 150 mph. Später flog er mit einer Durchschnittsgeschwindigkeit von 100 mph zurück in die erste Stadt. Die gesamte Flugzeit betrug 5 Stunden. Wie weit sind die Städte voneinander entfernt? Antwort: 300 Meilen

• Schrittweise Lösungen anzeigen

Wortaufgaben
Im Folgenden finden Sie einige Beispiele für Wortaufgaben, bei denen es um die Arbeit von Personen oder Maschinen geht.
Beispiel:
Maria braucht zehn Stunden, um vierzig Scheffel Äpfel zu pflücken. Kayla kann die gleiche Menge in 12 Stunden pflücken. Wie lange bräuchten sie, wenn sie zusammenarbeiten?

• Schrittweise Lösungen anzeigen

Word Problems Involving Work
Beispiele:
1. Ein erfahrener Maler braucht 6 Tage, um ein Haus zu streichen. Ein Lehrling braucht 8 Tage, um das gleiche Haus zu streichen. Wie lange würde es dauern, wenn sie zusammenarbeiten?
2. Ein Rohr kann einen Tank in 8 Stunden füllen. Ein anderes Rohr kann den Tank in 12 Stunden leeren. Wenn beide Rohre gleichzeitig geöffnet werden, wie lange würde es dauern, den Tank zu füllen?

• Schrittweise Lösungen anzeigen

Anwendungen, die Gleichungssysteme beinhalten
Nachfolgend finden Sie Beispiele für Anwendungen, die Gleichungssysteme oder das Lösen von simultanen Gleichungen beinhalten.

Beispiele:
1. Finde zwei Zahlen, bei denen die Summe 93 und die Differenz 9 ist.
2. Der Umfang eines Rechtecks ist 160 yd. Die Breite ist 4 mehr als die Hälfte der Länge. Finde die Länge und die Breite.
3. Sunset mietet einen 18-Fuß-Truck für 49,95 $ plus 75 Cent pro Meile. Cactus mietet einen 18-Fuß-Transporter für $59,95 plus 50 Cent pro Meile. Für welche Kilometerleistung sind die Kosten gleich hoch?

• Schrittweise Lösungen anzeigen

Beispiele:
1. Angenommen, alle Kurse am Pheonix College sind entweder 3 oder 4 Credits wert. Das Langlaufteam belegt insgesamt 40 Kurse, die 144 Credits wert sind. Wie viele 3-Credit-Kurse und wie viele 4-Credit-Kurse werden belegt?
2. HomeMart verlangt 3,50 $ für eine CFL-Glühbirne und Supply Depot verlangt 2,50 $ für eine CFL-Glühbirne, die nicht ganz so lange hält. Wenn Ihr Wohnkomplex die Rechnung verloren hat, aber sie wissen, dass sie 300 Glühbirnen gekauft und $885 ausgegeben haben, wie viele Glühbirnen wurden von jedem Geschäft gekauft.
3. Grounds Works berechnet $8,00/Pfund für Premium-Röstkaffee und $4,50/Pfund für Value-Röstkaffee. Wie viel von jeder Sorte sollte verwendet werden, um eine 10-lb-Mischung herzustellen, die $5,90/lb kosten würde?
4. Ein Zug verlässt Prescott, AZ, und fährt mit einer Geschwindigkeit von 25mph nach Norden zum Grand Canyon. Anderthalb Stunden später fährt ein Schnellzug auf einem Parallelgleis ab und fährt mit 60mph nach Norden. Wie weit vom Startbahnhof entfernt werden sie sich treffen?

• Schrittweise Lösungen anzeigen

Anwendungen, die Ungleichungen beinhalten
Im Folgenden finden Sie Beispiele für Algebra-Wortaufgaben, die Ungleichungen beinhalten
Beispiele:
1. Andrea hat 53,50 $ in der Tasche und möchte Hemden zu einem Verkaufspreis von 14,95 $ pro Stück kaufen.
Wie groß ist die Anzahl der Hemden, die sie kaufen kann? (Nehmen Sie an, dass die Hemden von der Umsatzsteuer befreit sind)
2. Das Dreifache einer um 8 erhöhten Zahl ist höchstens 40. Finde den größtmöglichen Wert der Zahl.
3. Die Länge eines Rechtecks ist 8 Meter kleiner als das Fünffache seiner Breite. Wenn der Umfang des Rechtecks höchstens 104 Meter beträgt, finde die größtmögliche Breite des Rechtecks.
4. Zwei aufeinanderfolgende Zahlen sind so, dass ihre Summe größer als 98 ist, vermindert um das Doppelte der größeren. Finden Sie die kleinstmöglichen Werte für die ganzen Zahlen.

• Schrittweise Lösungen anzeigen

Beispiel:
Eine Witwenfabrik hat feste Betriebskosten von 3.600 $ pro Tag und Kosten von 1,40 $ pro produziertem Widget. Wenn ein Widget für 4,20 $ verkauft wird, wie viele Widgets müssen pro Tag mindestens verkauft werden, um einen Gewinn zu erzielen?

• Schrittweise Lösungen anzeigen

Testen Sie den kostenlosen Mathway-Rechner und Problemlöser unten, um verschiedene mathematische Themen zu üben. Probieren Sie die vorgegebenen Beispiele aus, oder geben Sie Ihr eigenes Problem ein und überprüfen Sie Ihre Antwort mit den Schritt-für-Schritt-Erklärungen.