MatemáticasPrecálculo Matemáticas en Nebraska
Sección Estiramientos y Compresiones Horizontales
En el apartado anterior hemos hablado del resultado de multiplicar la salida de la función por un valor constante. Sin embargo, ¿qué ocurre cuando multiplicamos la entrada de la función? Para explorar esta idea, observamos las gráficas de
y discutimos cómo están relacionadas.
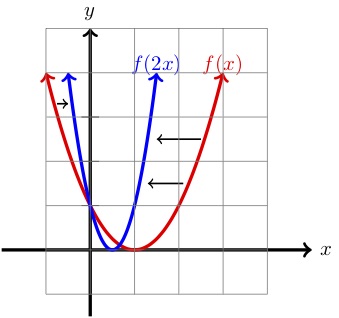
| (x) | (y=f(x)|) | (y=f(2x)|) | (-1\) | (4\) | (8\) |
| (-.5\N-( | (2.25\N-) | (4\N-) |
| (0\N-) | (1\N-) | (1\N-) |
| (.5\N-) | (.25) | (0) | (1) | (0) | (1) |
| (2) | (1) | (9) |
Como podemos ver arriba, en comparación con la gráfica de \(f(x)\text{,}) la gráfica de \(f(2x) \) está comprimida horizontalmente por un factor de \text{.Efectivamente, si se nos da un punto \((x,y) \) en la gráfica de \(f(x) \) entonces \ft(dfrac{1}{2}x,y\right) \) es un punto en la gráfica de \(f(2x)\text{.})
Mirando la tabla anterior podemos comprobar esto para unos cuantos puntos. Por ejemplo, el punto \((2,1)\Nestá en la gráfica de \N(f(x)\Ntexto{.}) Entonces
es un punto de la gráfica \f(f(2x)\text{.{\})
Estiramiento horizontal
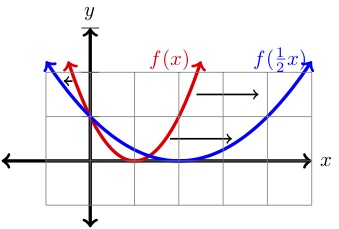
| (x\) | (y=f(x)\N) | (y=f\left(dfrac{1}{2}xright)\N) | (-1\) | (4\) | (2.25\) |
| (0) | (1) | (1) | |
| (1) | (0) | (.25\N-(td) | |
| (2) | (1) | (0) | |
| (4) | (9) | (1) |
La gráfica de \(f)-izquierda(\dfrac{1}{2}x)-derecha) se estira horizontalmente por un factor de \(2 \) en comparación con la gráfica de \(f(x) \text{.}\) Además, si \((x,y) \) es un punto en la gráfica de \(f(x)\text{,}\}) entonces \((2x,y) \) es un punto en la gráfica de \(f\left(dfrac{1}{2}x\\}right)\text{,})
Podemos ver esto en nuestro ejemplo anterior. Fíjate que \((2,1) \) es un punto en \(f(x)\text{,}\} y
es un punto en la gráfica de \(f\left(\dfrac{1}{2}x\right)\Ncomo se muestra en la tabla y la gráfica anteriores. En general tenemos:
Estiramientos, compresiones y reflexiones horizontales
En comparación con la gráfica de \(y = f (x)\text{,}\}, la gráfica de \(y = f (a\cdot x)\text{,}) donde \a \a 0\text{,}) está
- comprimida horizontalmente por un factor de \a \a} si \a \abs{a}gt 1\text{,
- se estira horizontalmente por un factor de \(\abs{dfrac{1}{a}}) si \(0\ltabs{a}lt 1\text{,}\}) y
- se refleja en el eje \(y\} (y se estira o se comprime) si \(a\lt 0\text{.}\})
Como habrás notado a estas alturas a través de nuestros ejemplos, un estiramiento o compresión horizontal nunca cambiará las intercepciones \(y\). Esta es una buena forma de saber si se ha producido dicha transformación.
Ejemplo272
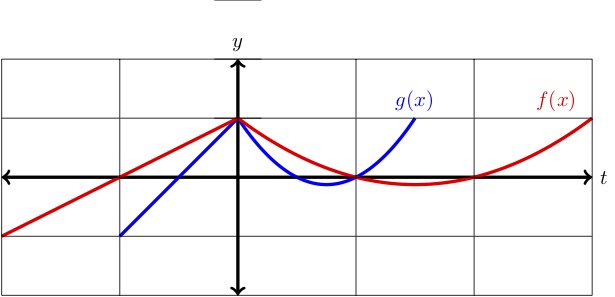
Se muestra la gráfica de \(f(x)\Njunto con un estiramiento horizontal de la compresión de \(f(x) \Ntexto.}\) Decide si \(g(x)\Nes un estiramiento o una compresión, y da una fórmula para \(g(x)\Nen términos de \(f(x)\Ntexto.})
Primero, notar que la intersección de la \ (y) se mantiene fija mientras que las intersecciones de la \ (x) se acercan al eje de la \ (y). Esto nos dice que \(g(x)\Nes una compresión horizontal. Las intersecciones \(x \) de \(f(x)\) son \(x=-1,1,2 \) mientras que las intersecciones \(x)\ de \(g(x)\) son \(x=-.5,.5,1\text.
Entonces, las intersecciones de \(x)-de \(g(x) \) pueden obtenerse tomando las intersecciones de \(f(x) \) y dividiendo cada una por 2. Esto nos dice que \(g(x)\) es una compresión horizontal por un factor de \(2 \text{.Por lo tanto, podemos escribir