MatematicaPreCalcolo Matematica al Nebraska
SezioneAllungamenti e compressioni orizzontali
Nella sezione precedente abbiamo discusso il risultato della moltiplicazione dell’uscita della funzione per un valore costante. Tuttavia, cosa succede quando moltiplichiamo l’input della funzione? Per esplorare questa idea, guardiamo i grafici di
e discutiamo come sono collegati.
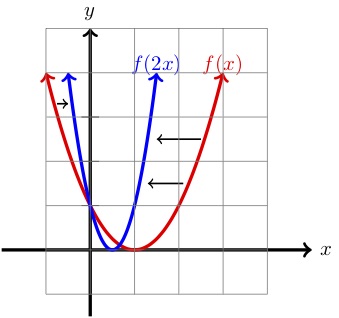
| \(x) | (y=f(x)\) | (y=f(2x)\) | ||
| \(-1) | (4) | (8) | ||
| (-.5) | (2.25) | (4) | ||
| (0) | (1) | (1) | ||
| (.5) | (.25) | (0) | ||
| (1) | (0) | (1) | ||
| (2) | (1) | (9) |
Come possiamo vedere sopra, rispetto al grafico di \(f(x)\text{,}) il grafico di \(f(2x) \) è compresso orizzontalmente di un fattore di \(2 \text{.In effetti, se ci viene dato un punto \((x,y) \) sul grafico di \(f(x) \) allora \(\left(\dfrac{1}{2}x,y\right) \) è un punto sul grafico di \(f(2x)\text{.})
Guardando la tabella sopra possiamo verificare questo per alcuni punti. Per esempio, il punto \((2,1)\) è sul grafico di \(f(x)\testo{.}) Allora
è un punto sul grafico \(f(2x)\testo{.
Tratto orizzontale
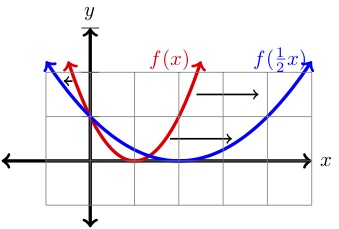
| \(x\) | (y=f(x)\) | (y=f\sinistra(\dfrac{1}{2}x\destra)\) | |||
| (-1) | (4) | (2.25) | |||
| (0) | (1) | (1) | |||
| (1) | (0) | (0) | (.25) | ||
| (2) | (1) | (0) | |||
| (4) | (9) | (1) |
Il grafico di \(f\left(\dfrac{1}{2}x\right)\) è allungato orizzontalmente di un fattore di \(2 \) rispetto al grafico di \(f(x) \text{.}\) Inoltre, se \((x,y) \) è un punto sul grafico di \(f(x)\text{,}}) allora \((2x,y) \) è un punto sul grafico di \(f\left(\dfrac{1}{2}x\right)\text{.})
Si può vedere questo nel nostro esempio sopra. Notate che \((2,1) \) è un punto su \(f(x)\text{,}}) e
è un punto sul grafico di \(f\sinistra(\dfrac{1}{2}x\destra)\) come mostrato nella tabella e grafico sopra. In generale abbiamo:
Allungamenti, compressioni e riflessioni orizzontali
Rispetto al grafico di \(y = f (x)\text{,}}) il grafico di \(y = f (a\cdot x)\text{,) dove \a \ne 0{,} è
- compresso orizzontalmente di un fattore pari a \(\abs{a}}) se \(\abs{a}}gt 1{,
- allungato orizzontalmente di un fattore pari a \(\abs{dfrac{1}{a}} se \(0lt{abs{a}}lt 1{,}}) e
- riflesso intorno all’asse \(y)-(e allungato o compresso) se \(a\lt 0{.Come avrete già notato attraverso i nostri esempi, un allungamento o una compressione orizzontale non cambierà mai le intercette di \(y). Questo è un buon modo per dire se una tale trasformazione è avvenuta.
Esempio272
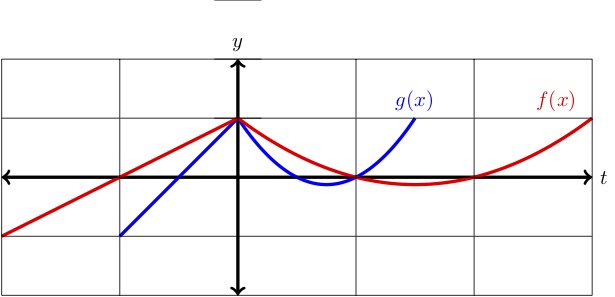
Il grafico di \(f(x)\ è mostrato insieme ad un tratto orizzontale di compressione di \(f(x) \text{.}\) Decidi se \(g(x) \ è un tratto o una compressione, e dai una formula per \(g(x)\ in termini di \(f(x)\text{.
Figura273 SoluzionePrima, notate che l’intercetta di \(y) rimane fissa mentre le intercette di \(x) si spostano più vicino all’asse di \(y). Questo ci dice che \(g(x)\) è una compressione orizzontale. Le intercette di \(x \) di \(f(x)\ sono \(x=-1,1,2 \) mentre le intercette di \(x \) di \(g(x)\ sono \(x=-.5,.5,1\text{.
Quindi, le intercette di \(x)\ di g(x) \ possono essere ottenute prendendo le intercette di \(f(x) \ e dividendole per 2. Questo ci dice che \(g(x)\ è una compressione orizzontale di un fattore di \(2 \testo{.}\a6) Quindi, possiamo scrivere
inizio{equazione*}g(x)=f(2x).\fine{equazione*}Figura274Esplora le proprietà di stiramenti e compressioni orizzontali discusse in questa sezione con questa applet. Puoi cambiare la funzione base \(f(x)\) usando la casella di input e vedere molti diversi allungamenti/compressioni di \(f(x)\) muovendo il cursore \(a\). SottosezioneEsercizi
1Esplorazione di compressioni e stiramenti orizzontali
2Descrizione di compressioni e stiramenti
3Punti sulle compressioni e gli allungamenti
4Graffigurare compressioni e allungamenti
5Dominio e intervallo di compressioni e allungamenti
6Applicazione: Conversioni in funzioni