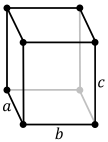
Sistema cristalino ortorrómbico
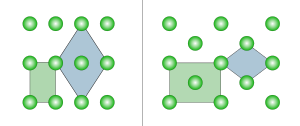
Editar en dos dimensiones
En dos dimensiones hay dos entramados ortorrómbicos de Bravais: rectangular primitivo y rectangular centrado. La red rectangular primitiva también puede describirse mediante una celda unitaria rómbica centrada, mientras que la red rectangular centrada también puede describirse mediante una celda unitaria rómbica primitiva.
Edición tridimensional
En tres dimensiones, existen cuatro redes ortorrómbicas de Bravais: ortorrómbica primitiva, ortorrómbica centrada en la base, ortorrómbica centrada en el cuerpo y ortorrómbica centrada en la cara.
| Ritual de Bravais | Ortorrómbica primitiva | Ortorrómbica centrada en la base .centrada ortorrómbica |
Centrada en el cuerpo ortorrómbica |
Face-centrada ortorrómbica |
Símbolo de Pearson | oP | oS | oI |
|---|---|---|---|---|
| Célula unitaria estándar | ||||
| Prisma rómbico recto célula unitaria |
 |
En el sistema ortorrómbico existe una segunda opción de ejes cristalinos poco utilizada que da lugar a una celda unidad con forma de prisma rómbico derecho; Se puede construir porque la capa base bidimensional rectangular también se puede describir con ejes rómbicos. En esta configuración de ejes, las celdas primitivas y centradas en la base se intercambian en el tipo de centrado, mientras que lo mismo ocurre con las celdas centradas en el cuerpo y en la cara. Obsérvese que la longitud a {\displaystyle a}

en la fila inferior no es la misma que en la fila superior, como puede verse en la figura de la sección de entramados bidimensionales. Para la primera y tercera columna de arriba, a {\displaystyle a}

de la segunda fila es igual a a 2 + b 2 {\displaystyle {\sqrt {a^{2}+b^{2}}}}

de la primera fila, y para la segunda y cuarta columna es igual a la mitad.