Applications de l’algèbre
Thèmes connexes:
Plus de leçons pour le GRE en mathématiques, feuilles de travail en mathématiques
Cette leçon fait partie d’une série de leçons pour la section raisonnement quantitatif du test général révisé du GRE. Dans cette leçon, nous allons apprendre :
- Applications de l’algèbre
- Traduction des mots en algèbre
- Exemples d’utilisation de l’algèbre pour résoudre des problèmes de mots
- Problèmes de mots de moyenne
- Problèmes de mots de mélange
- Distance, taux, Temps
- Problèmes de mots de travail
- Problèmes de mots qui impliquent des équations simultanées
- Problèmes de mots qui impliquent des inéquations
Applications de l’algèbre
Transcrire des descriptions verbales en expressions algébriques est une étape initiale essentielle pour résoudre des problèmes de mots.
Ces exemples sont donnés ci-dessous.
– Si le carré du nombre x est multiplié par 4, puis que 15 est ajouté à ce produit, le résultat peut être représenté par 4×2 + 15
– Si le salaire actuel s de Pierre est augmenté de 15 %, alors son nouveau salaire est de 1,15s.
– Si y gallons de jus d’orange doivent être distribués entre 5 personnes de façon à ce qu’une personne particulière obtienne 1 gallon et que le reste du jus soit divisé également entre les 4 autres, alors chacune de ces 4 personnes obtiendra (y – 1) ÷ 4
Cette vidéo montre comment traduire des mots et des expressions en expressions algébriques impliquant des variables.
Exemples d’utilisation des techniques algébriques pour résoudre des problèmes de mots
Nous allons maintenant montrer quelques exemples d’utilisation des techniques algébriques pour résoudre des problèmes de mots. Vous trouverez d’autres exemples de problèmes de mots algébriques ici. Problèmes de mots de moyenne
Les exemples suivants sont des exemples de problèmes de mots qui impliquent la moyenne ou la moyenne arithmétique.
Exemple 1:
Ellen a obtenu les notes suivantes à 3 examens : 82, 74 et 90. Quelle note
Ellen devra-t-elle obtenir au prochain examen pour que la note moyenne (moyenne arithmétique) des 4 examens soit de 85 ?
Laissons x représenter la note obtenue au prochain examen d’Ellen.
La moyenne des 4 examens est ![]()
En résolvant x, on obtient
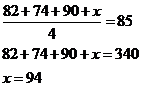
Par conséquent, Ellen devra atteindre une note de 94 à son prochain examen.
Exemple 2:
Lors de ses quatre premières parties, Jennifer a joué 101, 112, 126, 108. Quel est le score minimum qu’elle doit réaliser lors de sa cinquième partie pour avoir une moyenne d’au moins 110 ?
- Montrer les solutions étape par étape
Problèmes de mots sur les mélanges
Voici quelques exemples de problèmes de mots qui impliquent un mélange et une concentration de mélange.
Exemple 1:
Un mélange de 12 onces de vinaigre et d’huile contient 40 % de vinaigre, où toutes les
mesures sont en poids. Combien d’onces d’huile doivent être ajoutées au mélange pour produire un nouveau mélange qui n’est que de 25 pour cent de vinaigre ?
Laissons x représenter le nombre d’onces d’huile à ajouter. Alors le nombre total d’onces du nouveau mélange sera de 12 + x, et le nombre total d’onces de vinaigre dans le nouveau mélange sera de (0,40)(12). Comme le nouveau mélange doit être composé de 25 % de vinaigre, on obtient
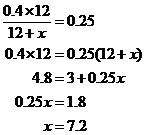
7,2 onces d’huile doivent être ajoutées pour produire un nouveau mélange composé de 25 % de vinaigre.
Exemple 2:
Une solution contient 15 % d’acide chlorhydrique. Quelle quantité d’eau faut-il ajouter à 50 ml de cette solution pour la diluer à une solution à 2 % ?
Problèmes de mots de distance, de taux, de temps
Voici quelques exemples de problèmes de mots de distance, de taux, de temps.
Exemple 1:
Dans une compétition de conduite, Jeff et Dennis ont parcouru le même parcours à des vitesses moyennes de 51
miles par heure et 54 miles par heure, respectivement. Si Jeff a mis 40 minutes pour parcourir le parcours, combien de temps a-t-il fallu à Dennis ?
Disons que x est le temps, en minutes, qu’il a fallu à Dennis pour parcourir le parcours. La distance d, en miles, est égale au produit du taux r, en miles par heure, et du temps t, en heures ; c’est-à-dire, d = rt
Notez que puisque les taux sont donnés en miles par heure, il est nécessaire d’exprimer les temps en heures ; par exemple, 40 minutes égalent ![]() d’une heure.
d’une heure.
En utilisant la formule, d = rt, nous pouvons obtenir le tableau suivant.
|
Distance |
Taux |
Heure |
|
|
Jeff |
51 × |
|
|
|
Dennis |
54 × |
|
Puisque les distances sont égales,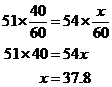
Il a fallu à Dennis environ 37.8 minutes pour parcourir le parcours. Une introduction à la résolution de problèmes de mots sur le mouvement uniforme (taux-temps-distance) en utilisant la formule taux x temps = distance, ou rt=d.
Exemple :
Deux cyclistes partent du même coin et roulent dans des directions opposées. Un cycliste roule deux fois plus vite que l’autre. En 3 heures, ils sont séparés de 81 miles. Trouve la vitesse de chaque cycliste. Réponse : 9 mph et 18 mph.
- Solutions étape par étape
Problème de mots utilisant la formule rt=d du mouvement uniforme
Exemple :
Un joggeur a commencé à courir à une vitesse moyenne de 6 mph. Une demi-heure plus tard, un autre coureur a commencé à courir après lui en partant du même endroit à une vitesse moyenne de 7 mph. Combien de temps faudra-t-il au coureur pour rattraper le joggeur ? Réponse : 3 heures.
- Voir les solutions étape par étape
Problème de mots utilisant la formule rt=d du mouvement uniforme
Exemple :
Un trajet de 555 miles et 5 heures sur l’Autobahn a été effectué à deux vitesses. La vitesse moyenne de la voiture était de 105 mph sur la première partie du voyage, et la vitesse moyenne était de 115 mph pour la deuxième partie. Combien de temps la voiture a-t-elle roulé à chaque vitesse ? Réponse : 105 mph pendant 2 heures et 115 mph pendant 3 heures.
- Montrer les solutions étape par étape
Problème de mots utilisant la formule rt=d du mouvement uniforme
Exemple :
Andy et Beth sont aux extrémités opposées d’une route de campagne de 18 miles avec des plans pour partir au même moment en courant l’un vers l’autre pour se rencontrer. Andy court à 7 mph tandis que Beth court à 5 mph. Combien de temps après leur départ se rencontreront-ils ? Réponse : 1,5 heure.
- Voir les solutions étape par étape
Exemple :
Une voiture et un bus partent à 14h du même endroit, dans la même direction. La vitesse moyenne de la voiture est le double de celle du bus. Après 2 heures, la voiture a 68 miles d’avance sur le bus. Trouvez la vitesse du bus et de la voiture. Réponse : Vitesse du bus : 34 mph ; Vitesse de la voiture : 68 mph.
- Montrer les solutions étape par étape
Exemple :
Un pilote a volé d’une ville à une autre ville à une vitesse moyenne de 150 mph. Plus tard, il a volé de nouveau vers la première ville à une moyenne de 100 mph. La durée totale du vol a été de 5 heures. Quelle distance sépare les deux villes ? Réponse : 300 miles
- Montrer les solutions étape par étape
Problèmes de mots sur le travail
Voici quelques exemples de problèmes de mots qui impliquent un travail effectué par des individus ou des machines.
Exemple:
Il faut à Maria dix heures pour ramasser quarante boisseaux de pommes. Kayla peut ramasser la même quantité en 12 heures. Combien de temps leur faudrait-il s’ils travaillaient ensemble ?
Problèmes de mots impliquant le travail
Exemples:
1. Il faut 6 jours à un peintre expérimenté pour peindre une maison. Il faut 8 jours à un apprenti pour peindre la même maison. Combien de temps leur faudrait-il s’ils travaillaient ensemble ?
2. Un tuyau peut remplir un réservoir en 8 heures. Un autre tuyau peut vider le réservoir en douze heures. Si les deux tuyaux sont ouverts simultanément, combien de temps faudra-t-il pour remplir le réservoir ?
Applications qui impliquent des systèmes d’équations
Voici des exemples d’applications qui impliquent des systèmes d’équations ou la résolution d’équations simultanées.
Exemples :
1. Trouvez deux nombres dont la somme est 93 et la différence est 9.
2. Le périmètre d’un rectangle est de 160 yd. La largeur est de 4 plus de la moitié de la longueur. Trouvez la longueur et la largeur.
3. Sunset loue un camion de 18 pieds pour 49,95 $ plus 75 cents par kilomètre. Cactus loue une camionnette de 18 pieds pour 59,95 $ plus 50 cents par mille. Pour quel kilométrage le coût est-il le même ?
- Montrer les solutions étape par étape
Exemples :
1. Supposons que tous les cours du collège Pheonix valent soit 3, soit 4 crédits. L’équipe de cross-country suit un total de 40 cours qui valent 144 crédits. Combien de cours à 3 crédits et combien de cours à 4 crédits sont suivis ?
2. HomeMart facture 3,50 $ pour une ampoule CFL et Supply Depot facture 2,50 $ pour une ampoule CFL qui ne dure pas aussi longtemps. Si votre complexe d’appartements a perdu la facture, mais qu’ils savent qu’ils ont acheté 300 ampoules et dépensé 885 $, combien d’ampoules ont été achetées dans chaque magasin.
3. Grounds Works facture 8 $/lb pour le café à torréfaction premium et 4,50 $/lb pour le café à torréfaction value. Quelle quantité de chaque type devrait être utilisée pour faire un mélange de 10 lb qui coûterait 5,90 $/lb ?
4. Un train quitte Prescott, AZ et se rend au nord du Grand Canyon à une vitesse de 25 mph. Une heure et demie plus tard, un train express part sur une voie parallèle et se déplace vers le nord à 60 mph. À quelle distance de la gare de départ se rencontreront-ils ?
- Montrer les solutions étape par étape
Applications qui impliquent des inégalités
Les exemples suivants sont des exemples de problèmes de mots d’algèbre qui impliquent des inégalités
Exemples:
1. Andrea a 53,50 $ en poche et veut acheter des chemises au prix de solde de 14,95 $ chacune.
Quel est le plus grand nombre de chemises qu’elle peut acheter ? (Supposez que les chemises sont exemptes de la taxe de vente)
2. Trois fois un nombre augmenté de 8 est au plus 40. Trouvez la plus grande valeur possible de ce nombre.
3. La longueur d’un rectangle est inférieure de 8 mètres à 5 fois sa largeur. Si le périmètre du rectangle est au maximum de 104 mètres, trouver la plus grande largeur possible du rectangle.
4. Deux nombres consécutifs sont tels que leur somme est supérieure à 98 diminuée de deux fois le plus grand. Trouvez les plus petites valeurs possibles pour ces nombres entiers.
- Montrer les solutions étape par étape
Exemple:
Une usine de widgets a un coût d’exploitation fixe de 3 600 $ par jour plus des coûts de 1,40 $ par widget produit. Si un widget se vend 4,20 $, quel est le nombre minimal de widgets qui doivent être vendus par jour pour réaliser un bénéfice ?
Essayez la calculatrice et le résolveur de problèmes gratuits Mathway ci-dessous pour vous exercer à divers sujets mathématiques. Essayez les exemples donnés, ou tapez votre propre problème et vérifiez votre réponse avec les explications étape par étape. 

