Inversion matricielle : Trouver l’inverse d’une matrice

Retourner à l’index des leçons | Faire les leçons dans l’ordre | Page facile à imprimer

Inversion de matrice :
Déterminer l’inverse d’une matrice (page 1 sur 2)

Pour les matrices, la division n’existe pas. Vous pouvez ajouter, soustraire et multiplier des matrices, mais vous ne pouvez pas les diviser. Il existe cependant un concept connexe, qui s’appelle « inversion ». Je vais d’abord discuter de la raison pour laquelle l’inversion est utile, puis je vous montrerai comment la faire.

Repensez à l’époque où vous avez appris pour la première fois comment résoudre des équations linéaires. Si on vous donnait quelque chose comme  » 3x = 6 « , vous le résoudriez en divisant les deux côtés par 3. Comme multiplier par1/3 revient à diviser par 3, vous pourriez aussi multiplier les deux côtés par 1/3 pour obtenir la même réponse : x = 2. Si vous deviez résoudre quelque chose comme  » (3/2)x = 6 « , vous pourriez toujours diviser les deux côtés par 3/2, mais il était probablement plus facile de multiplier les deux côtés par 2/3. La fraction réciproque 2/3 est l’inverse de 3/2 car, si vous multipliez les deux fractions, vous obtenez 1, ce qui est, dans ce contexte, appelé « l’identité (multiplicative) » : 1 est appelé l’identité parce que multiplier quelque chose par 1 ne change pas sa valeur.

Cette terminologie et ces faits sont très importants pour les matrices. Si l’on vous donne une équation matricielle comme AX = C, où l’on vous donne A et C et on vous demande de calculer X, vous aimeriez  » diviser  » la matrice A. Mais vous ne pouvez pas faire de division avec les matrices. En revanche, que se passerait-il si vous pouviez trouver l’inverse de A, un peu comme pour trouver la fraction réciproque ci-dessus ? L’inverse de A, écrit sous la forme  » A-1  » et prononcé  » A inverse « , vous permettrait d’annuler le A de l’équation matricielle, puis de résoudre X.

AX = C
A-1AX = A-1C
IX = A-1C
X = A-1C

Comment  » A-1AX  » du côté gauche de l’équation s’est-il transformé en  » X  » ? Repensez à la nature des inverses pour les nombres réguliers. Si vous avez un nombre (comme 3/2) et son inverse (dans ce cas, 2/3) et que vous les multipliez, vous obtenez 1. Et 1 est l’identité, appelée ainsi parce que 1x = x pour tout nombre x. Cela fonctionne de la même manière pour les matrices. Si vous multipliez une matrice (comme A) et son inverse (dans ce cas,
A-1), vous obtenez la matrice identité I. Et l’intérêt de la matrice identité est que IX = X pour toute matrice X (ce qui signifie « toute matrice de taille correcte », bien sûr).

Il faut noter que l’ordre dans la multiplication ci-dessus est important et n’est pas du tout arbitraire. Rappelons que, pour les matrices, la multiplication n’est pas commutative. C’est-à-dire que AB n’est presque jamais égal à BA. Ainsi, multiplier l’équation matricielle « à gauche » (pour obtenir A-1AX) n’est pas du tout la même chose que multiplier « à droite » (pour obtenir AXA-1). Et vous ne pouvez pas dire que le produit AXA-1 est égal à A-1AX, car vous ne pouvez pas intervertir l’ordre de la multiplication. Au lieu de cela, vous devez multiplier A-1 sur la gauche, en le plaçant juste à côté du A dans l’équation matricielle d’origine. Et comme vous devez faire la même chose des deux côtés d’une équation lorsque vous la résolvez, vous devez également multiplier « à gauche » du côté droit de l’équation, ce qui donne A-1C. Vous ne pouvez pas être désinvolte avec votre placement des matrices ; vous devez être précis, correct et cohérent. C’est la seule façon de réussir à annuler A et à résoudre l’équation matricielle.

Comme vous l’avez vu ci-dessus, les matrices inverses peuvent être très utiles pour résoudre les équations matricielles. Mais, étant donné une matrice, comment l’inverser ? Comment trouver l’inverse ? La technique d’inversion des matrices est plutôt astucieuse. Pour une matrice donnée A et son inverse A-1, nous savons que nous avons A-1A = I. Nous allons utiliser la matrice identité I dans le processus pour inverser une matrice.

• Trouver l’inverse de la matrice suivante.

D’abord, j’écris les entrées la matrice A, mais je les écris dans une matrice double largeur :

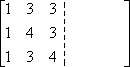
Dans l’autre moitié de la double-largeur, j’écris la matrice identité :

Maintenant, je vais faire des opérations de ligne de matrice pour convertir le côté gauche du double-large en l’identité. (Comme toujours avec les opérations de rangée, il n’y a pas une seule « bonne » façon de le faire. Ce qui suit ne sont que les étapes qui me sont venues à l’esprit. Vos calculs pourraient facilement être très différents.)

Maintenant que le côté gauche du double-large contient l’identité, le côté droit contient l’inverse. Autrement dit, la matrice inverse est la suivante :

Notez que nous pouvons confirmer que cette matrice est l’inverse de A en multipliant les deux matrices et en confirmant que nous obtenons l’identité : Copyright © Elizabeth Stapel 2003-2011 Tous droits réservés

Sachez que, dans la  » vraie vie « , l’inverse est rarement une matrice remplie de jolis nombres entiers bien nets comme celui-ci. Avec un peu de chance, cependant, surtout si vous faites des inverses à la main, on vous en donnera de jolis comme celui-ci à faire.

Top | 1 | 2 | Retour à l’index Suivant >>

.