Système cristallin orthorhombique
Deux dimensionsEdit
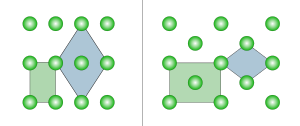
En deux dimensions, il existe deux treillis orthorhombiques de Bravais : rectangulaire primitif et rectangulaire centré. Le treillis rectangulaire primitif peut également être décrit par une cellule unitaire rhombique centrée, tandis que le treillis rectangulaire centré peut également être décrit par une cellule unitaire rhombique primitive.
Trois dimensionsEdit
En trois dimensions, il existe quatre treillis de Bravais orthorhombiques : orthorhombique primitif, orthorhombique centré sur la base, orthorhombique centré sur le corps et orthorhombique centré sur la face.
| Réseau de Bravais | Primitif orthorhombique |
Base-.centrée orthorhombique |
Centrée du corps orthorhombique |
Face-centrée orthorhombique |
|---|---|---|---|---|
| Symbole de Pearson | oP | oS | oI | oF |
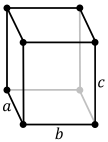
| cellule unitaire standard |
 |
 |
 |
 |
| Prisme rhombique droit cellule unitaire |
 |
 |
 |
Dans le système orthorhombique, il existe un second choix d’axes cristallins rarement utilisé qui aboutit à une cellule unitaire ayant la forme d’un prisme rhombique droit ; Il peut être construit parce que la couche de base bidimensionnelle rectangulaire peut également être décrite avec des axes rhombiques. Dans cette configuration d’axes, les treillis primitifs et centrés sur la base échangent leur type de centrage, tandis que la même chose se produit avec les treillis centrés sur le corps et centrés sur la face. Notez que la longueur a {\displaystyle a}

dans la rangée inférieure n’est pas la même que dans la rangée supérieure, comme on peut le voir dans la figure de la section sur les treillis bidimensionnels. Pour la première et la troisième colonne ci-dessus, a {\displaystyle a}

de la deuxième rangée est égal à a 2 + b 2 {\displaystyle {\sqrt {a^{2}+b^{2}}}}

de la première ligne, et pour la deuxième et la quatrième colonne, elle est égale à la moitié de celle-ci.
